3 声学物理基础
3.1 机械振动和机械波
产生机械波的条件
- 有机械振动的波源
- 能传播波的弹性介质
描述一个机械波
- 波幅
- 频率:通常波动频率在数值上等于波源振动频率
- 波速:仅由介质决定,一般比质点振动快
- 波长:\(\lambda = c\cdot T\)
- 相位
一般用
\[
p = p_a\cos(\omega t-kx+\varphi)
\]
来描述一个波,其中\(p_a\)是声压的振幅,\(k = \frac{2\pi}{\lambda}\)是波矢
3.2 声波和分类
根据质点振动方向
- 纵波:凡是能受拉/压的介质都能传播
- 横波:仅固体能传播,因为只有固体能受剪切力
- 表面波:椭圆运动,短轴在传播方向
根据波阵面分类
由于能量守恒,能流\(I\)与面积\(S\)的乘积不变,而\(I\propto A^2\),那么波幅\(A\)与传播距离\(r\)的关系是
平面波:\(A\)不随\(r\)变化,波源是一个平面
柱面波:\(A\propto \frac{1}{\sqrt{r}}\),波源是一条直线
球面波:\(A\propto \frac{1}{r}\),波源是一个点
平面圆片换能器发射的超声波:离换能器近的区域,认为是平面波;远的区域,认为是球面波
同样的,太阳光是平面波而星光是球面波
根据振动持续时间
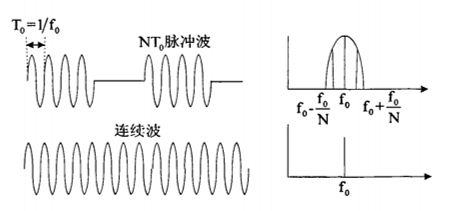
连续波
脉冲波,视为连续波乘矩形窗
3.3 声学参量
3.3.1 声速
给定介质的声速是个常量,但受温度和波型的影响
声速与介质的密度反相关,弹性模量正相关,固体中还与泊松比有关
根据声速随水温的变化还能用声速反推温度
声速的本质:反映了介质受声扰动时的压缩特性,记为
\[
c^2 = \left(\frac{dp}{d\rho}\right)_S
\]
其中\(S\)表示绝热过程,若介质可压缩性较大(\(p\)变化不大而\(\rho\)变化大),那么声速就较低
3.3.2 声压
定义为声波引起的压强差
\[
p = P - P_0
\]
前者是当前压强,后者是静态压强,有
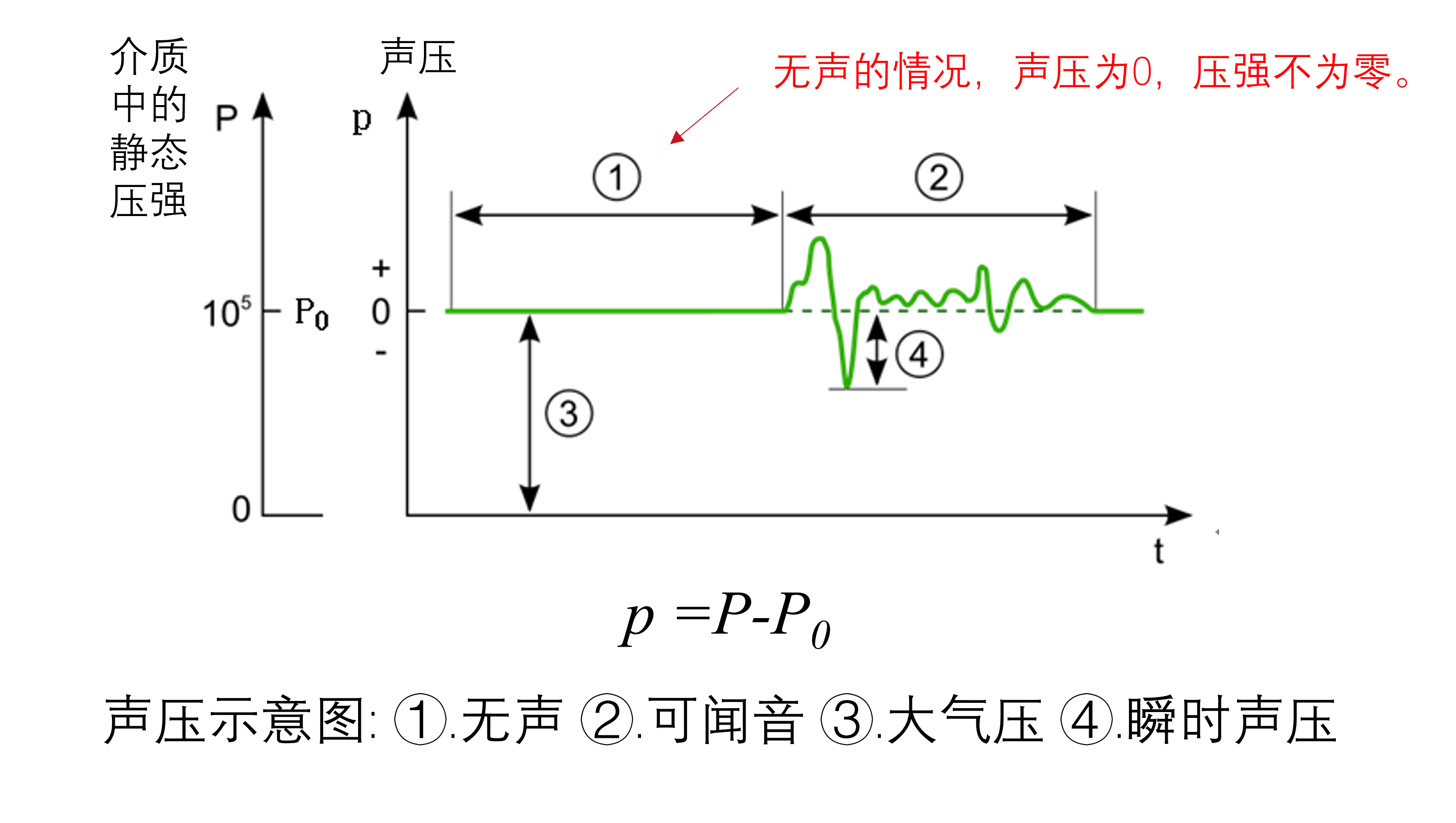
有效声压:瞬时声压的方均根
\[
p_e = \sqrt{\frac{1}{T}\int _T p^2dt}
\]
平面余弦波的\(p_e = \frac{\sqrt{2}}{2}p_a\)
声压级
用分贝表示
\[
L_p = 20\lg{\frac{p}{p_0}} \,\,\,\mathsf{dB}
\]
其中\(p_0=2\times 10^{-5}\mathsf{Pa}\),是基准声压,对应于1000Hz下人耳能听到的最低声压
用奈培表示
\[
L_n = \ln {\frac{p_1}{p_0}} \,\,\,\mathsf{Np}
\]
二者的换算关系为 1 Np / cm = 8.686 dB / cm
3.3.3 质点振动速度
注意与声波速度区分
一维声波的质点振动速度可以通过牛顿第二定律推导
\[
\rho \frac{dv}{dt} = -\frac{dp}{dx}
\]
其中\(\rho\)是介质密度,分为静态密度\(\rho_0\)和扰动下的密度变化,在线性声波下可以认为密度不变
\(p = p_a \cos{(\omega t-kx+\varphi)}\)是声压,于是得到
\[
v = -\frac{1}{\rho_0} \int \frac{dp}{dx}dt = \frac{p_a}{\rho_0 c}\cos(\omega t -kx+\varphi)
\]
其中\(c\)是波速
3.3.4 声阻抗和声阻抗率
声阻抗:界面声压与通过界面的声通量之比
\[
Z_a = \frac{p}{U} = \frac{p}{vS} = R_a + jX_a
\]
\(R_a\)表示能量传递,\(X_a\)表示存储在介质中的能量(不传播)
声阻抗率:归一化,最能反映介质声学特性的量
\[
Z_s = \frac{p}{v} = Z
\]
带入\(v\)的表达式,得到
\[
Z = \rho_0 c
\]
波速\(c\)能用绝热压缩系数表示为\(c = \frac{1}{\sqrt{\rho_0 K}}\),那么
\[
Z = \sqrt{\frac{\rho_0}{K}}
\]
一般而言,声阻抗率是复数;但是对无衰减的平面波,声阻抗率是一个与频率无关的实数
此时声阻抗率完全由介质决定
3.3.5 声强
声强:单位面积上的声功率
\[
I(t) = p(t)\cdot v(t)
\]
在稳态声场中,用一段时间的平均值来表示
对于平面余弦波,其平均声强为
\[
I = \frac{1}{2}\rho_0 cA^2\omega^2 = \frac{p_a^2}{2\rho_0c}=\frac{p_a^2}{2Z}
\]
其中\(A\)是质点振幅,\(A = \frac{p_a}{\omega \rho_0 c}\)
声强级
\[
L_I = 10\lg \frac{I}{I_0} \,\,\,\mathsf{dB}
\]
从20变为10的原因是\(I\propto p_a^2\)
3.3.6 声功率
\[ W = \int_S IdS \]
声强在一个面上的通量
声功率级
\[
L_W = 10\lg\frac{W}{W_0}
\]
3.4 生物组织的声学特性
声阻抗率最能反映生物组织的声学特性
生物组织之间的声速差不大,不超过5%;脂肪声速小于水,其他生物组织与水相近;骨骼和固体类似
生物组织的超声特性
- 似水组织
- 多脂类组织
- 骨骼等固体组织
- 肺泡、肠胃气等含气生物组织
主要区别是声阻抗率