12 原片换能器声场分析
圆片换能器模型如下所示
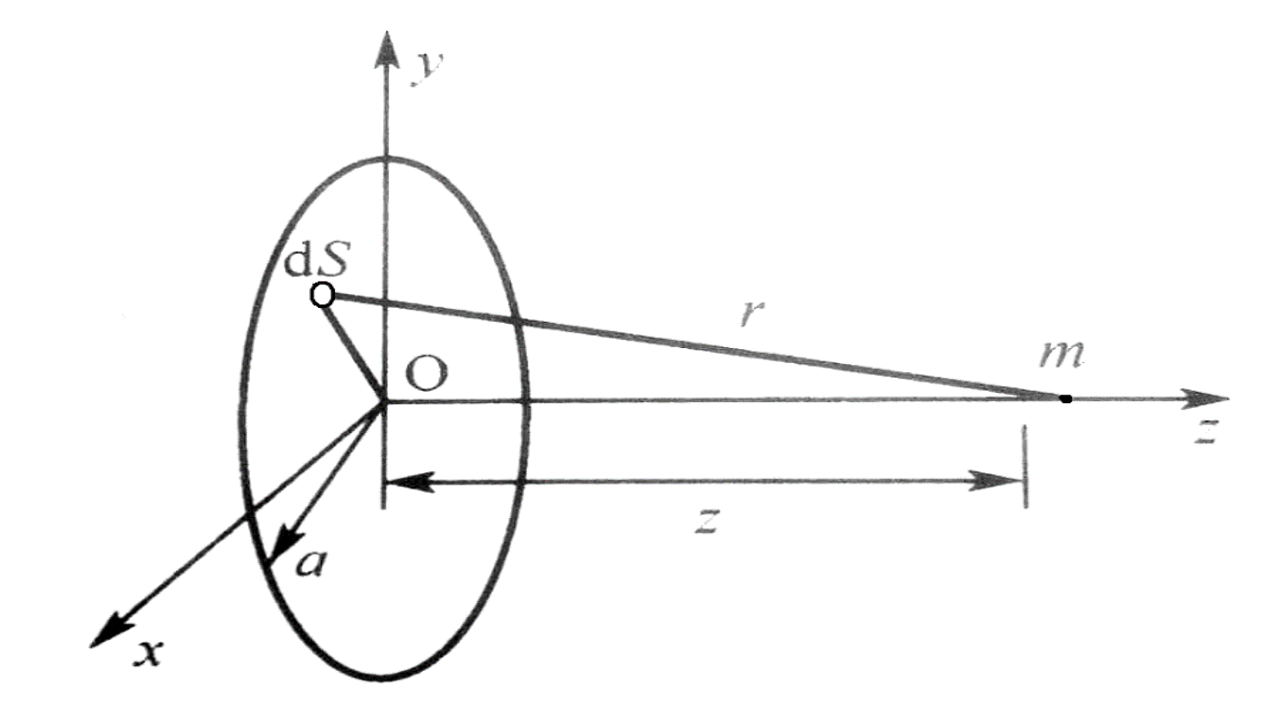
对于片上一个小面元\(dS\),视为一个点声源球面波,考虑波幅衰减,其声压沿轴线方向的分布为
\[
dp = \frac{kp_a}{2\pi r}\cos{\left(\omega t -kr+\frac{\pi}{2}\right)}dS \tag{1}
\]
其中\(\omega,k,r\)分别是声波的圆频率,波矢和传播距离
已知振元的振速\(u_a\),介质的声阻抗率\(z_c\),根据\(z_c=\rho_0c, u_a = \frac{p_a}{\rho_0 c}\),得到\(p_a = z_cu_a\)
假定振元距圆心距离为\(R\),那么\(dS=RdRd\theta\),在这个环形微元上的声压传播到m点时,沿轴线的分量完全相同
对式1进行积分,得到
\[
p_z = \int_S dp = \int_0^{2\pi} d\theta \int_0^a \frac{kz_cu_a}{2\pi \sqrt{R^2+z^2}}\cos{\left(\omega t -k\sqrt{R^2+z^2}+\frac{\pi}{2}\right)} RdR\\= p_a \left[ \cos\left(\omega t -k\sqrt{z^2+a^2}\right) -\cos\left( \omega t-kz \right)\right]
\]
将结果写为指数的形式,得到
\[
p_z = \frac{p_a}{2}\left\{ \left[ e^{i\left(\omega t-k\sqrt{z^2+a^2}\right)}+e^{-i\left(\omega t-k\sqrt{z^2+a^2}\right)} \right]- \left[ e^{i\left(\omega t-kz\right)}+e^{-i\left(\omega t-kz\right)} \right]\right\}\\
= \frac{p_a}{2}\left\{ e^{i\omega t}e^{-i\left( \frac{k\sqrt{z^2+a^2}+kz}{2} \right)}\left[ e^{i\left( \frac{-k\sqrt{z^2+a^2}+kz}{2} \right)}-e^{-i\left( \frac{-k\sqrt{z^2+a^2}+kz}{2} \right)} \right] +e^{-i\omega t}e^{i\left( \frac{k\sqrt{z^2+a^2}+kz}{2} \right)}\left[ e^{-i\left( \frac{-k\sqrt{z^2+a^2}+kz}{2} \right)}-e^{i\left( \frac{-k\sqrt{z^2+a^2}+kz}{2} \right)} \right] \right\}
\]
利用欧拉公式写为
\[
p_z = -2u_az_c \sin{\left(\frac{kz-k\sqrt{z^2+a^2}}{2}\right)}\sin\left( \omega t-\frac{k\sqrt{z^2+a^2}+kz}{2} \right) \tag{2}
\]
式2就是沿轴线的声压随时间的变化
现在考虑声压幅值
\[
p_m = -2u_az_c \sin{\left(\frac{kz-k\sqrt{z^2+a^2}}{2}\right)} \tag{3}
\]
由于\(z\gg a, z\gg \frac{3a^2}{2\lambda}\),利用等价无穷小\(\lim\limits_{x\rightarrow 0}(1+\alpha x)^n-1 = \alpha nx\)将正弦内部化简,得到
\[
\lim\limits_{z\gg a}-\frac{kz}{2}\left( 1-\sqrt{1+\frac{a^2}{z^2}} \right) =\frac{k}{4}\cdot\frac{a^2}{z} = \frac{\pi a^2}{2\lambda z} \tag{4}
\]
再根据\(\lim\limits_{x\rightarrow 0}\sin x = x \),将式4代入式3得到
\[
p_m = \frac{u_az_c\pi a^2}{\lambda z} = \frac{u_az_c S}{\lambda z} \tag{5}
\]
其中\(S\)是圆片的面积,令\(u_az_c \triangleq p_0\)代入式5,得到最终的表达式
\[
p_m = \frac{p_0S}{\lambda z}
\]
通过式3可以得知,当距离\(z\)满足
\[
Z_\max = \frac{4a^2-\lambda^2(2m+1)^2}{4\lambda (2m+1)}\,\,,\,\, Z_\min =\frac{a^2-\lambda^2m^2}{2m\lambda}
\]
时分别取最大/小值
定义最后一个极大值位置为近场到远场的临界距离,即\(m=0\)时的值
\[
Z_N = \frac{4a^2-\lambda^2}{4\lambda}
\]
指向性函数
任意方向上的声压幅值\(p_\theta\)与最大方向上的声压幅值\(p_0\)之比,即
\[
D_s = \frac{p_\theta}{p_0} = \frac{2J_1(ka\sin\theta)}{ka\sin\theta}
\]
其中\(J_1\)是一阶柱贝塞尔函数
波瓣图
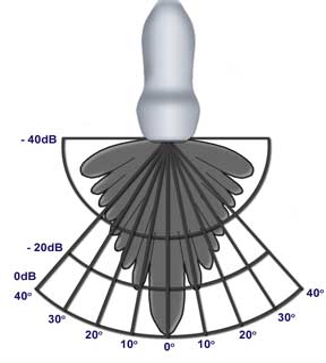
第一旁瓣与主瓣差-20dB,以最大值归一化
通过一阶柱贝塞尔函数的0点,可以估计声压幅值为0的位置,进而求出主瓣的半径为
\[ \theta_0 = 2\arcsin\left( \frac{0.61\lambda}{a} \right) \]
波瓣图反映
- 频率越高,主瓣越窄,旁瓣个数越多
- 圆片面积越大,主瓣越窄
- \(\theta_0\)定义为主瓣的方向锐度角
- 有时也用半功率面来划分主瓣,就是做一个-3dB的面