7 激光原理
重点:
激光器的组成和工作原理
如何克服受激辐射与受激吸收、自发辐射的矛盾
7.1 激光原理
原子的能级是量子化的
\[hv=E_2-E_1\]
自发辐射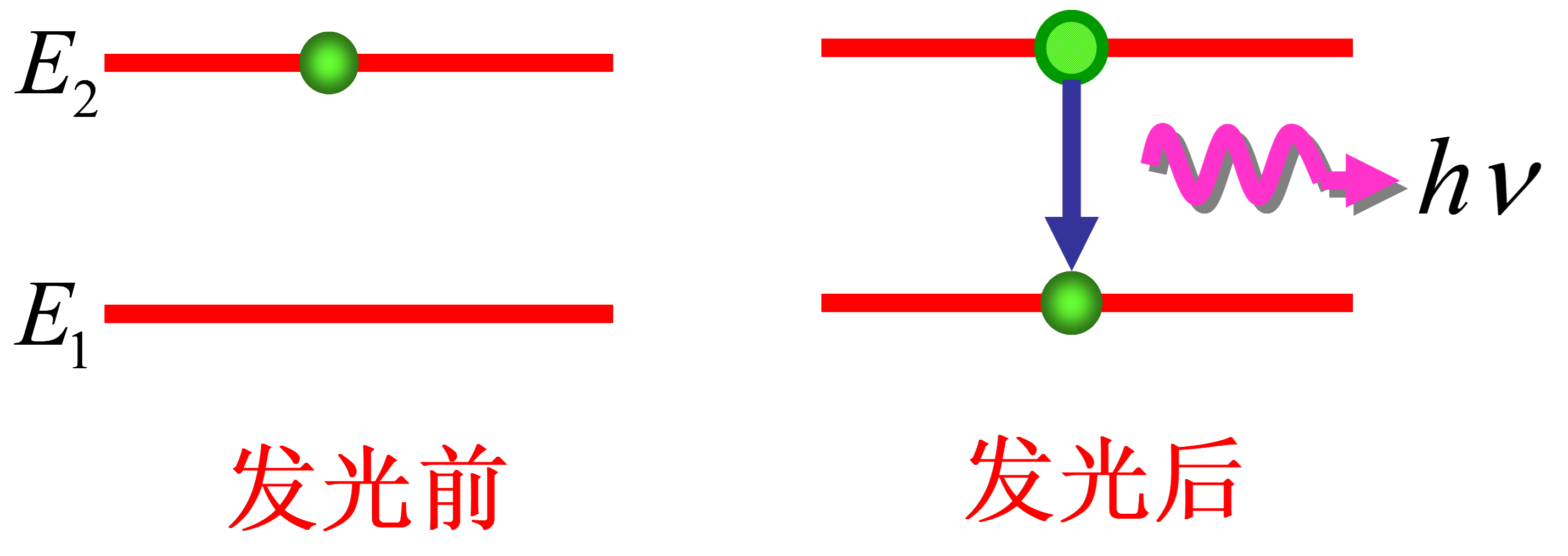
定义自发跃迁的几率(自发跃迁爱因斯坦系数)
\(A_{21}=(\frac{dn_{21}}{dt})_{sp}\cdot\frac{1}{n_2}\),其中sp表示spontaneous,表示单位时间内从2跃迁到1的电子占2总数的比例
def \(A_{21}=\frac{1}{\tau_s}\),其中\(\tau_s\)是原子在2的平均寿命,故\(A_{21}\)只和原子本身有关
受激吸收
定义受激吸收几率
\(W_{12}=(\frac{dn_{12}}{dt})_{st}\cdot\frac{1}{n_1}\),其中st表示stimulated
def \(W_{12}=B_{12}\rho_\nu\),\(B_{12}\)是受激吸收跃迁爱因斯坦系数,只与原子本身有关,\(\rho_{\nu}\)是辐射能量场密度
受激辐射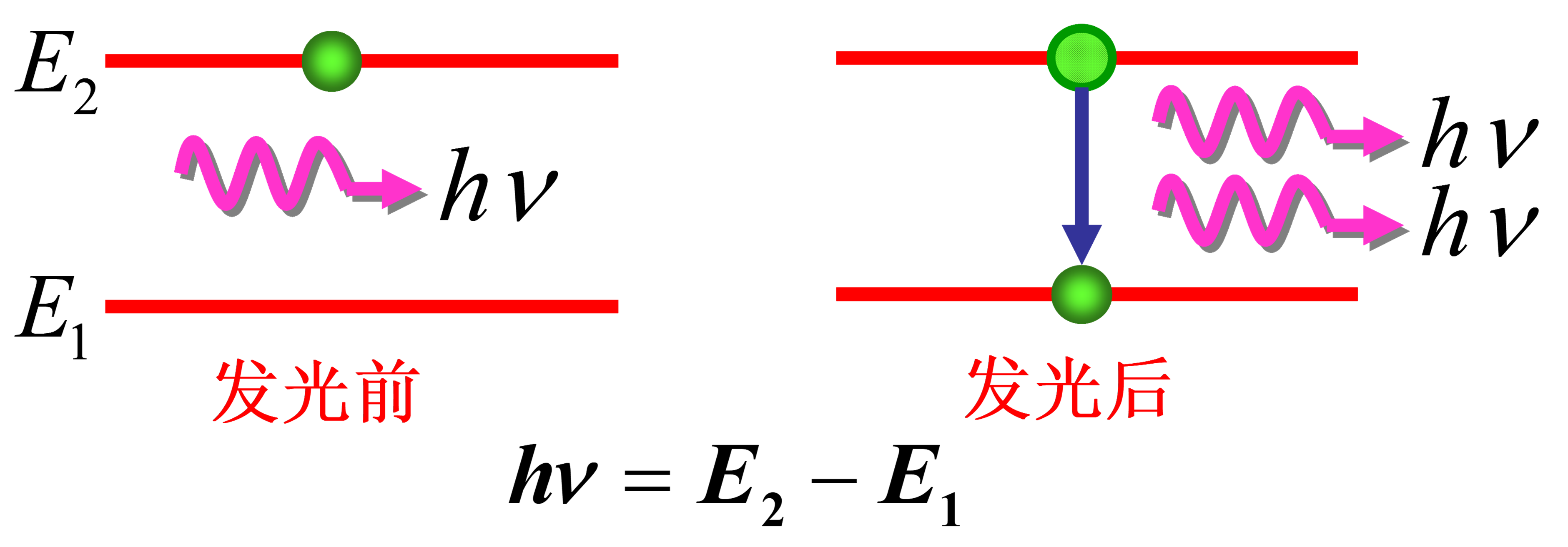
定义受激辐射几率
\(W_{21}=(\frac{dn_{21}}{dt})_{st}\cdot\frac{1}{n_2}\)
高能级的电子,在外来光子的激发下,向低能级跃迁而发光(进1出2)
受激产生的光子完全是入射光子的copy,二者频率,相位,波矢,偏振完全一致,有相同的光波模式(激光的相干性强)
def \(W_{21}=B_{21}\rho_\nu\)
受激辐射光放大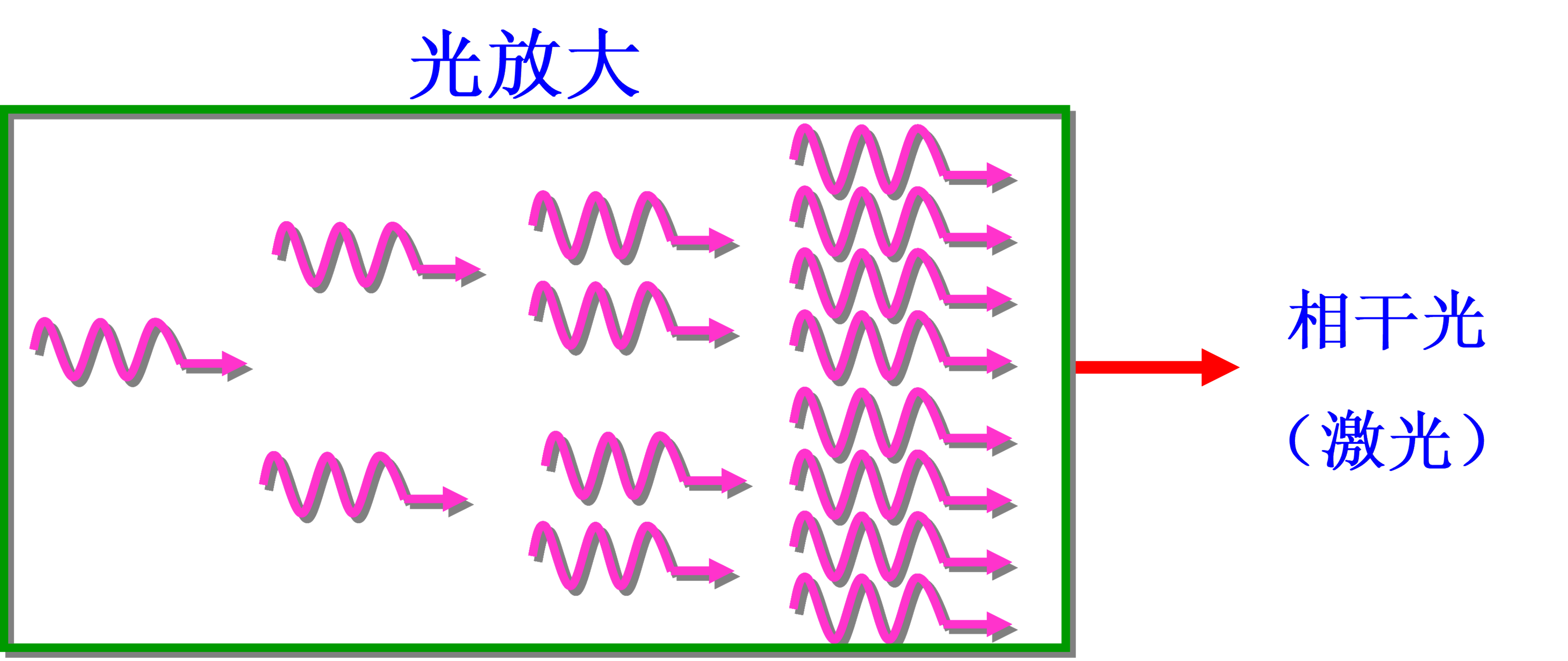
\(A_{21},B_{12},B_{21}\)的关系
在热平衡状态,辐射率等于吸收率,有\(n_2A_{21}+n_2B_{21}\rho_{\nu}=n_1B_{12}\rho_\nu\)
直接给出结论,\(B_{12}=B_{21},W_{12}=W_{21},A_{21}=\frac{8\pi h\nu^3}{c^3}B_{21}\)
7.2 受激辐射和受激吸收、自发辐射的矛盾
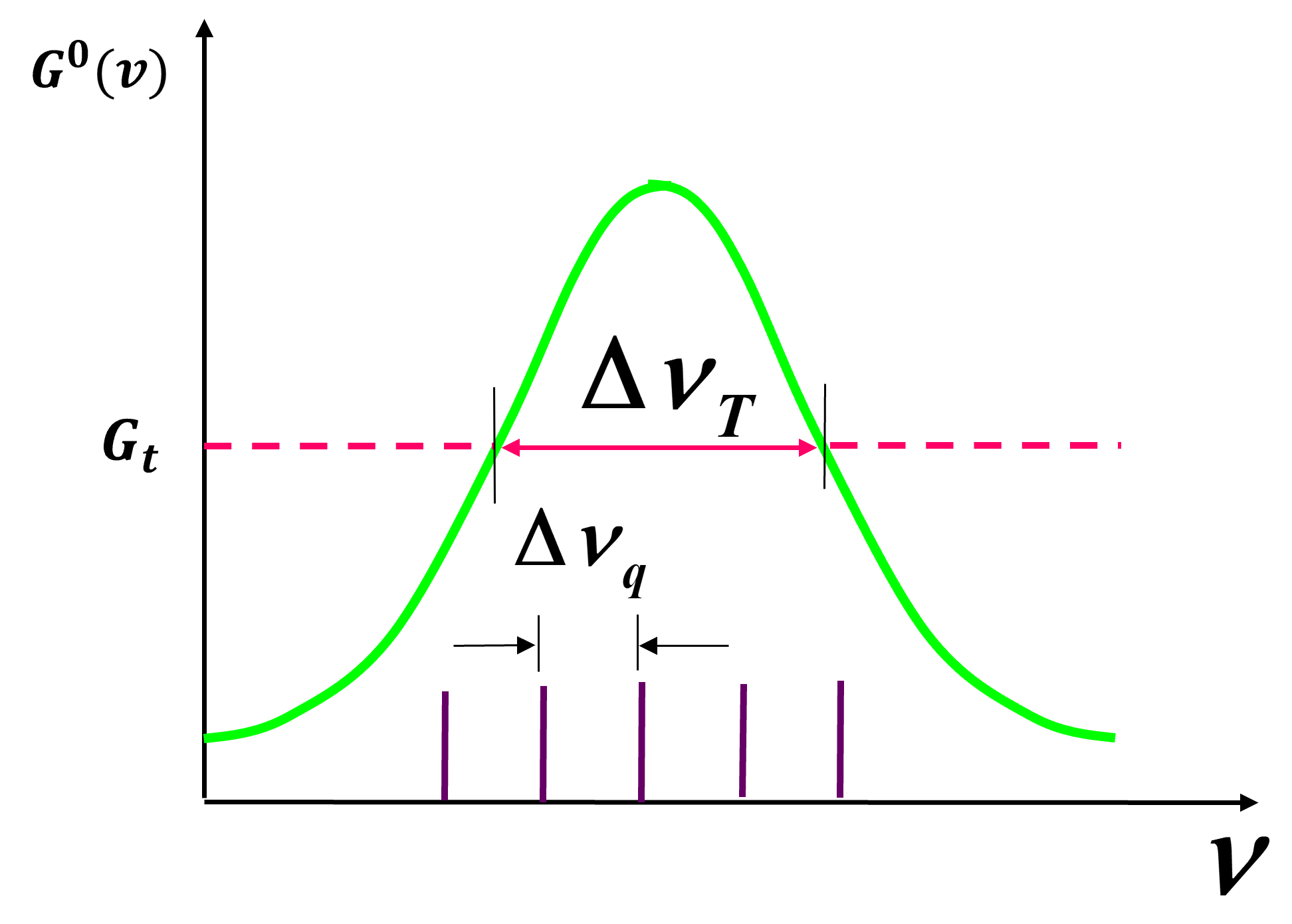
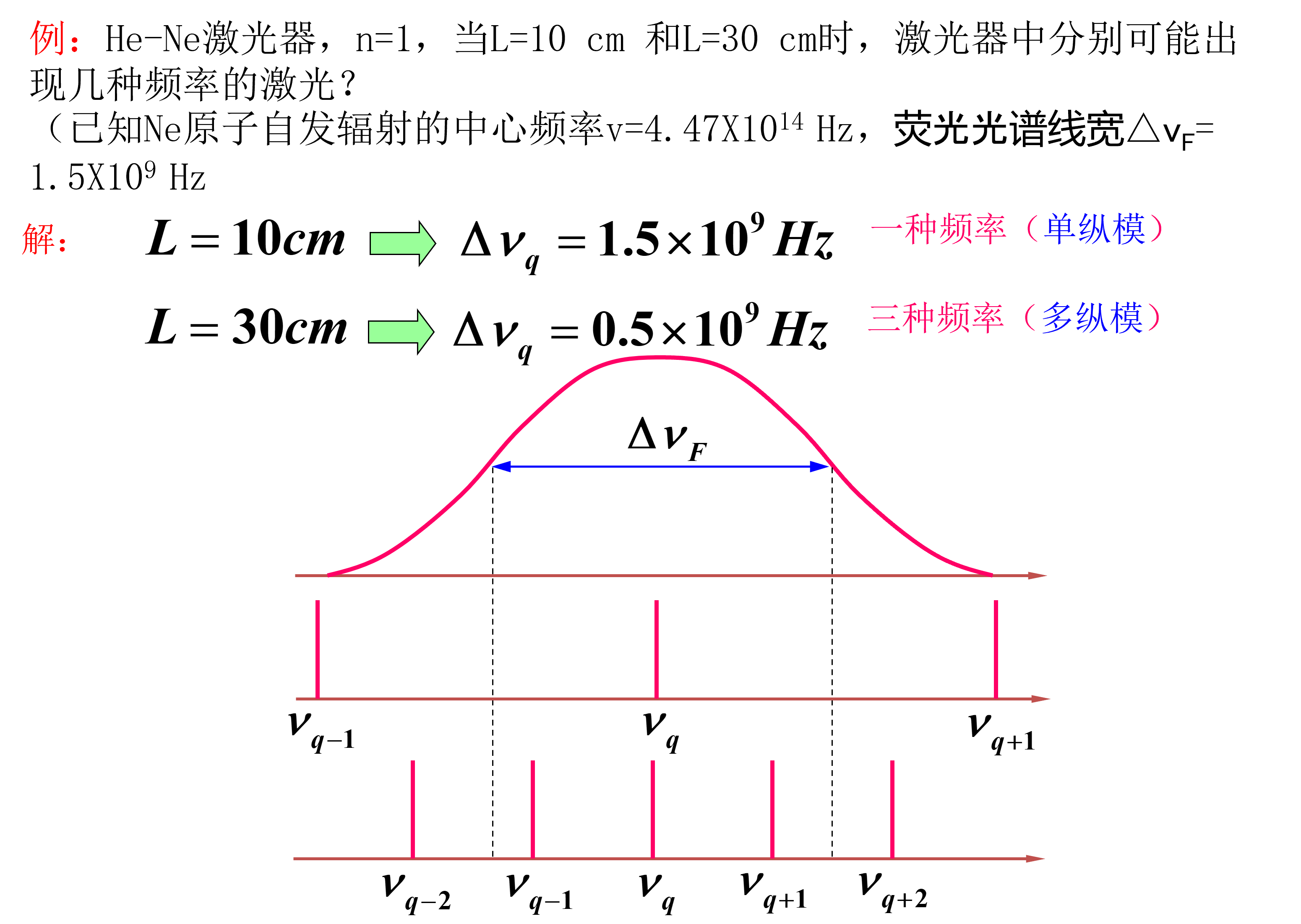
与受激吸收 如何克服 激活粒子的能级系统 三能级系统 图中E3是激发态,会快速衰减为E2亚稳态,E2和E1形成集居数反转 四能级系统 图中E4是激发态,E3&E2是亚稳态,E2会快速衰减为E1,E2相当于一个空能级,\(n_2\approx 0\) 与自发辐射 如何克服 光学谐振腔 光子在受激辐射的过程中会逐渐增多,当增长谐振腔\(\rho_\nu\)变大,就有可能达到\(B_{21}\rho_\nu>A_{21}\) 使用的光学谐振腔 在部分反射镜面上出射 增益系数\(g(z)=\frac{dI(z)}{dz}\cdot \frac{1}{I(z)}\),当\(I< 激光器中的光强变化\(dI(z)=[g(I)-\alpha]I(z)dz\) 振荡条件:\(I(z)=I_0e^{(g_0-\alpha)z}\geq I_0 \Rightarrow g_0\geq\alpha\) 基本组成 激光模式 共振腔的结构决定模式特征 驻波和谐振频率 明明在受激时已经确定了频率,为什么还会有谐振条件呢? 理想情况下,一个纵模对应一个谐振频率值,实际上存在带宽 起振纵模数 其中\(\Delta\nu_T\)是带宽,\(g 例:见图 可见\(\nu_T/\nu\)是非常小的,故认为中心处必有一个纵模,向两边间隔\(\Delta \nu\)计算个数
受激辐射过程光子数变多,受激吸收过程光子数变少
由于辐射要求电子在高能级,这必然导致**\(n_2
需要使得\(n_2>n_1\),即集居数反转,显然需要外界提供能量(Pumping,泵浦),使1先向2跃迁
称处于集居数反转的物质为激活物质
首先论证二能级系统无法实现:
当辐射稳定时,一定有:\(\frac{dn_2}{dt}=W(n_1-n_2)-n_2A_{21}=0 \Rightarrow \frac{n_2}{n_1}=\frac{W}{A_{21}+W}<1\)
需要引入亚稳态(不如基态稳定,但比激发态稳定得多)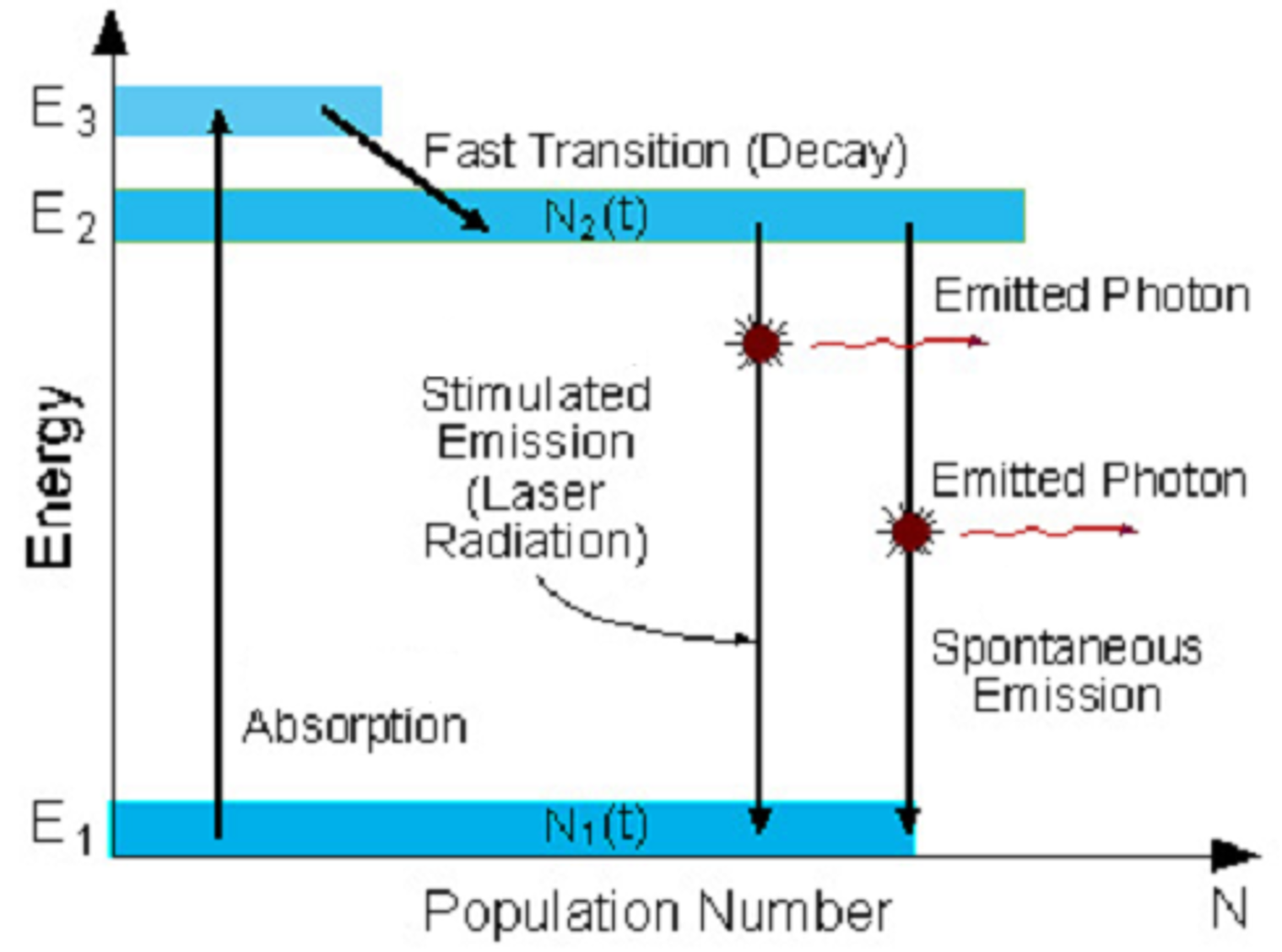
但是这样有一个问题,由于E2全部来自E3,需要将大量的E1先Pumping到E3,能耗太高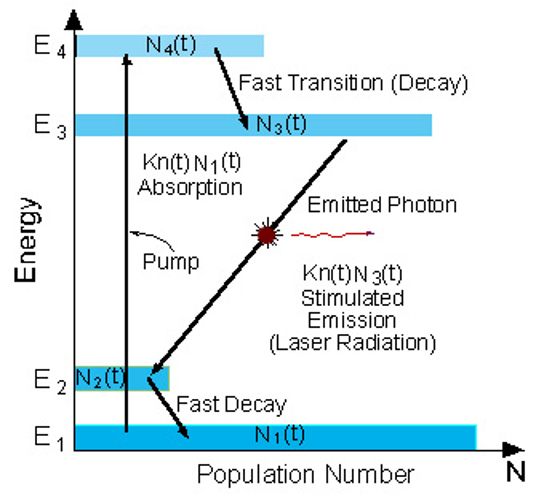
E3却不会快速衰减为E2,即\(n_3>>n_2\),用E3和E2组成新的激发系统
这样,只需要Pumping很少的电子到E3,就能形成集居数反转
def \(R=\frac{W_{21}}{A_{21}}\),表示辐射光子中受激和自发的比值,得到\(R\approx 10^{-35}\),完全可以忽略
即相干光子很少,无法生存
达到\(W_{21}=B_{21}\rho_\nu>A_{21}\),使受激光子在竞争中存活(但是引起受激辐射的光子最初来自自发辐射)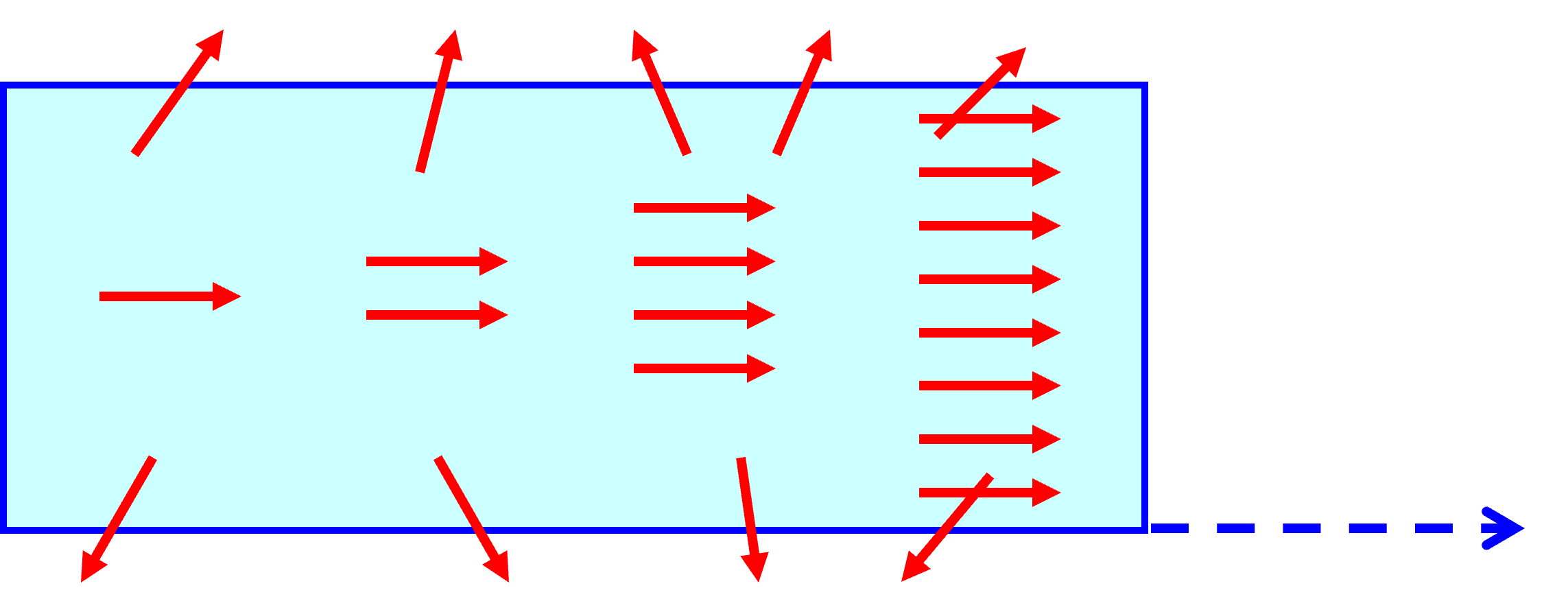
但是谐振腔不可能做的很长,使用反射镜面来增加光程,来回来回中受激光子就变多了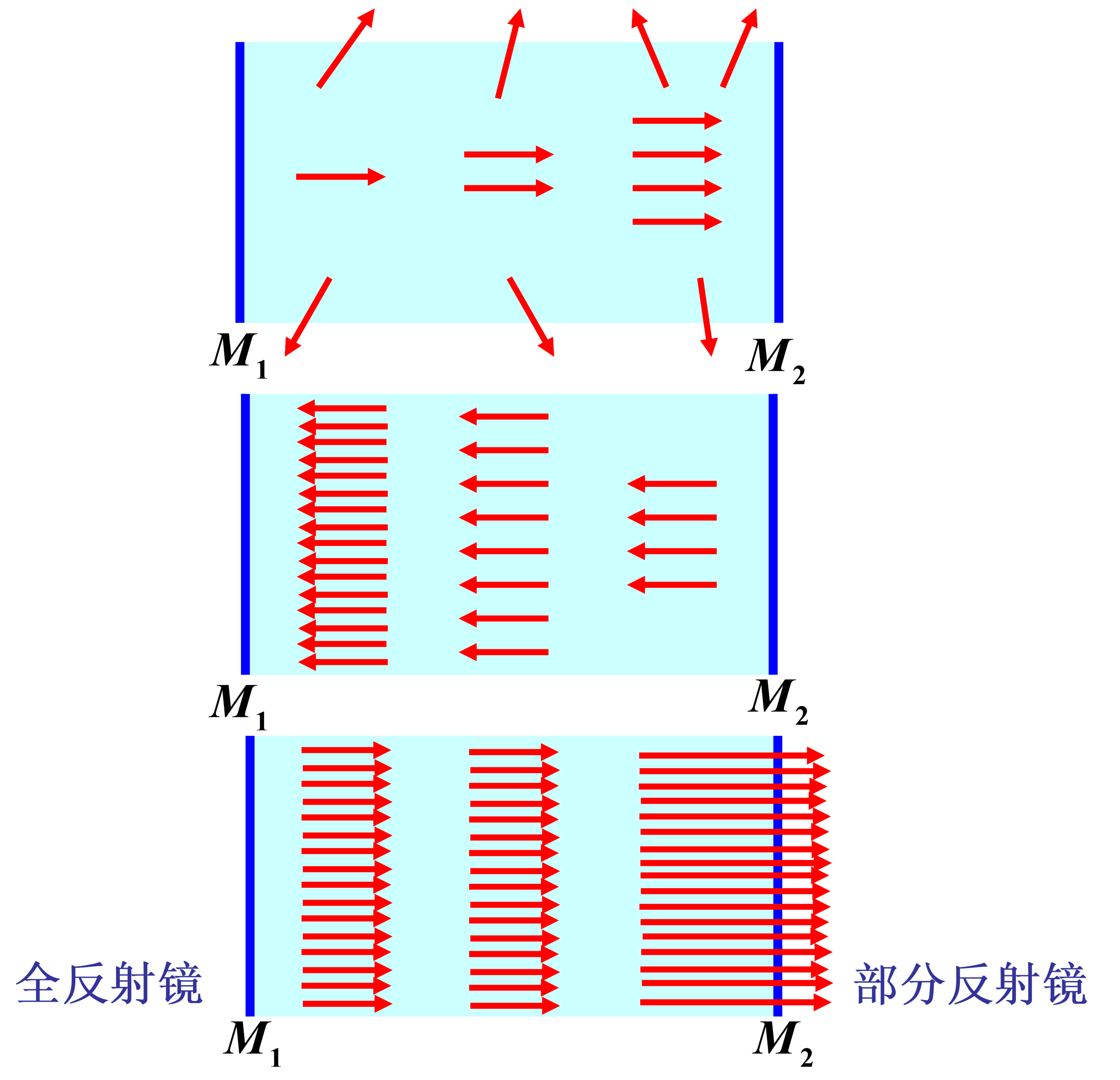
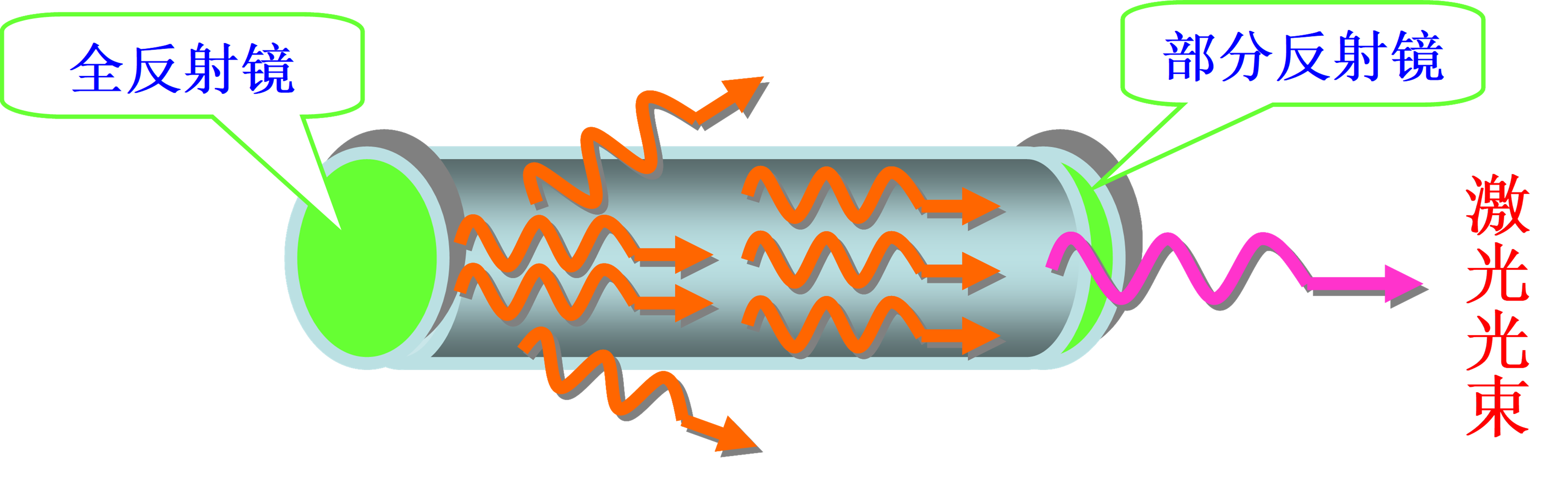
由于两块镜面平行放置,对光子的方向选择很强,偏了的光子会逸出腔外,平行的光子会变多
所以激光由高度方向性7.3 光子振荡条件
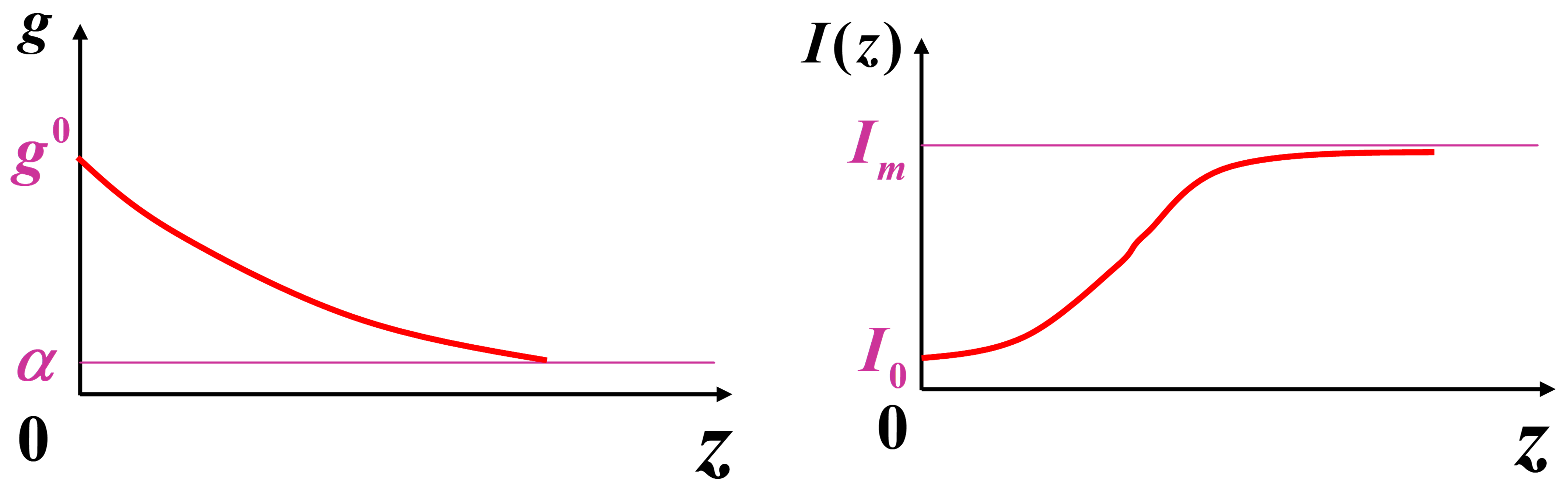

当满足上述条件时,无论初始的光强多小,都能形成\(I_m\)的光7.4 激光器的基本组成和分类

当激光器处于振荡状态时,激光器内部的光是满足一定相位条件的驻波
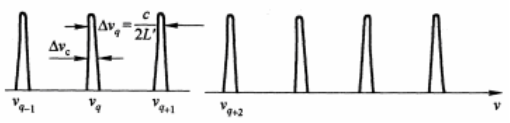
驻波条件:\(\Delta\phi=k\Delta x=\frac{2\pi}{\lambda}\cdot 2nl=2m\pi \Rightarrow l=m\cdot\frac{\lambda}{2n}\),其中n是介质折射率,\(m\in \mathbb{Z}\)
谐振条件:\(\nu=m\cdot\frac{c}{2nl}\)
纵模间隔:\(\Delta\nu=\frac{c}{2nl}\)
最终只有满足谐振条件的光子存活(因为增益最大)
因为原子的能级不是确定的,用能带更好理解,频率是一个小区间