6 光学基础

重点：

光医学的应用范围和发展历史
光的干涉、衍射和偏振
光学显微系统的分辨率极限

6.1 光的散射

瑞利散射
散射粒子线度比波长小很多，1/10波长以下。
散射光强度满足\(I(W)\varpropto W^4=\lambda^{-4}\)

米氏散射
散射粒子线度大于10倍波长，散射光强度与波长无关

为何是蓝天白云：
蓝天：大气中分子线度小，是瑞利散射，蓝光的强度大
白云：云中水颗粒线度大，是米氏散射，强度均一

6.2 几何光学

研究光在介质中传播和物体成像规律的学科

基本定律：

1. 光沿直线传播
2. 光的反射定律和折射定律
3. 独立传播及光路可逆

折射定律
\[n_1 \sin{\theta_1}=n_2 \sin{\theta_2}\]
全反射临界角\(\theta_c=\arcsin{\frac{n_2}{n_1}}\)，注意要从光密到光疏

透镜成像规律
\[\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\]，其中u为物距，v为像距，f为焦距
放大镜成虚像，增加物体对眼睛的视角

6.3 波动光学

详见大物二笔记

惠更斯-菲涅尔原理
光在传播过程中，在波阵面外任一点光振动应该是波阵面上所有子波相干叠加的结果

光的干涉
两束平面波\(E_1=E_{10}\cdot e^{i(\vec{k_1}\vec{r_1}-\omega_1 t-\phi_1)},E_2=E_{20}\cdot e^{i(\vec{k_2}\vec{r_2}-\omega_2 t-\phi_2)}\)，叠加后\(E=E_1+E_2\)
叠加波的光强\(I=E\cdot E^*=I_1+I_2+2\sqrt{I_1I_2}\cos{(\vec{k_1}\vec{r_1}-\vec{k_2}\vec{r_2}-(\omega_1-\omega_2) t-(\phi_1-\phi_2))}\)
当且仅当两束波的偏振在同一平面内才有上式
进一步，当：\(\omega_1=\omega_2,\phi_1-\phi_2\)是常数时，两束波稳定叠加，产生干涉，有
\[I=I_1+I_2+2\sqrt{I_1I_2}\cos{(k(r_1-r_2)+\Delta\phi)}\]
若是\(I_1=I_2=I_0\)，则有\(I=4I_0\cos^2{\frac{k(r_1-r_2)+\Delta\phi}{2}}\)
在实际应用中，还要满足两束波的光程差\(\Delta nl\)不超过波列的长度（不能超过相干长度，产生于单色性不足）
当光屏距离光源足够远时，\(r_1-r_2\approx \frac{x}{D}\cdot d\)，其中x是点的位置，D为光源到光屏距离，d是光源间距
所以得到最简式：\(I=4I_0\cos^2{\frac{\pi d}{\lambda D}x}\)

由上式可知，当\(x=n\frac{\lambda D}{d}\)时，干涉增强，亮条纹；当\(x=(n+\frac{1}{2})\frac{\lambda D}{d}\)时，干涉减弱，暗条纹
有：干涉条纹表示光程差的等值线；相邻干涉条纹之间的光程差为\(\lambda\)，相位差为\(2\pi\)

光的衍射

1. 夫琅禾费衍射：光源和光屏都在无穷远处
2. 菲涅尔衍射：o.w.

这部分详见大物二，要求不高
知道衍射是干涉的产物即可

光学系统的分辨率

圆孔衍射条纹（艾里斑）
中央亮斑称为艾里斑，其半径满足\(r_0=\frac{1.22\lambda}{d}l\)，其中d是光源距离，l透镜到光屏距离

实际上的光学系统如下图，可以认为夫琅禾费衍射，事实上其光强分布和衍射完全一致，其分辨率受到限制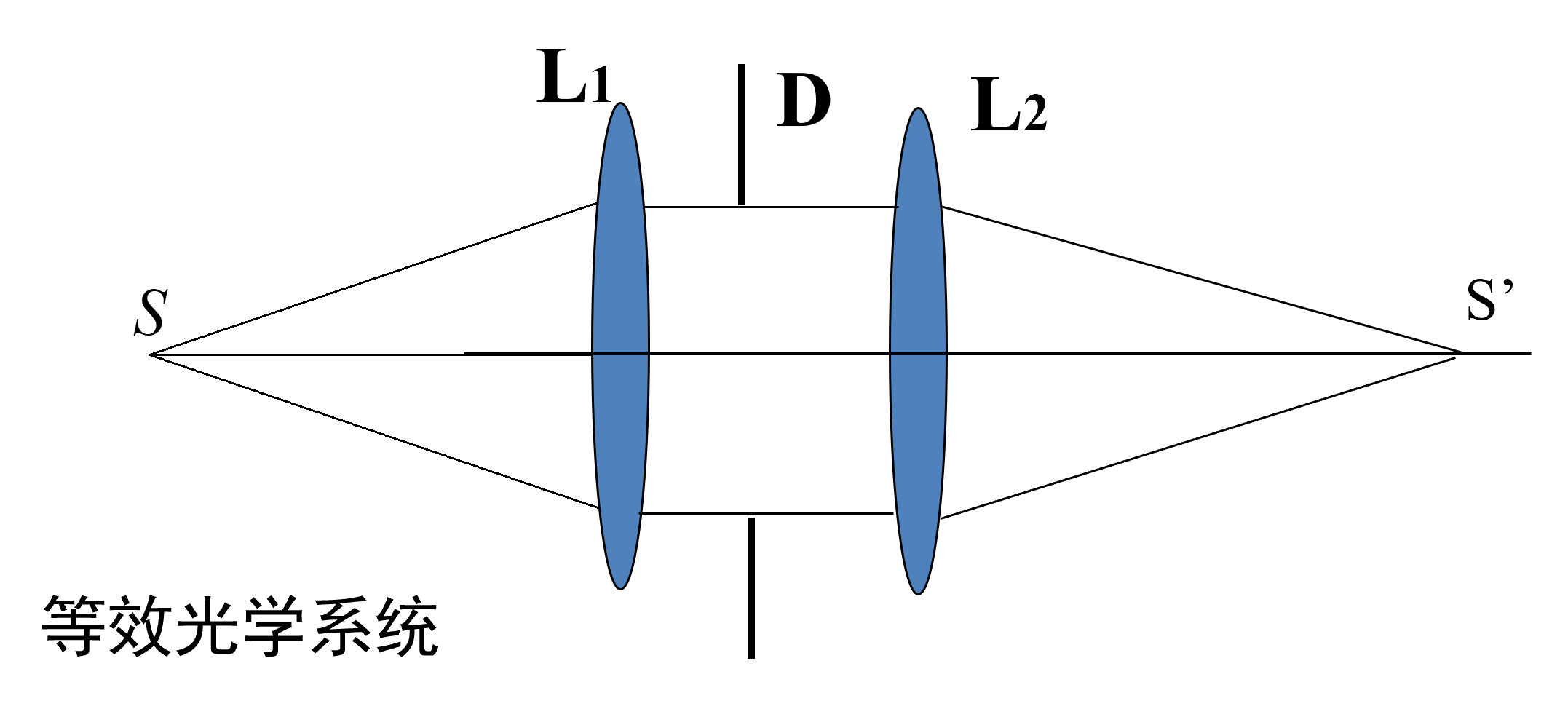

瑞利判据
当一个光斑的主极大和另一个的第一极小重合时，两个点刚好被分辨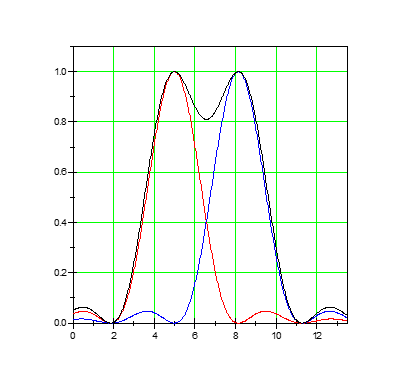

此时有最小分辨角\(\delta\theta=\frac{r_0}{l}=1.22\frac{\lambda}{d}\)，分辨率\(R=\frac{1}{\delta\theta}\)

光学系统的分辨率

阿贝正弦条件：\(nh\sin{u}=n'h'\sin{u'}\)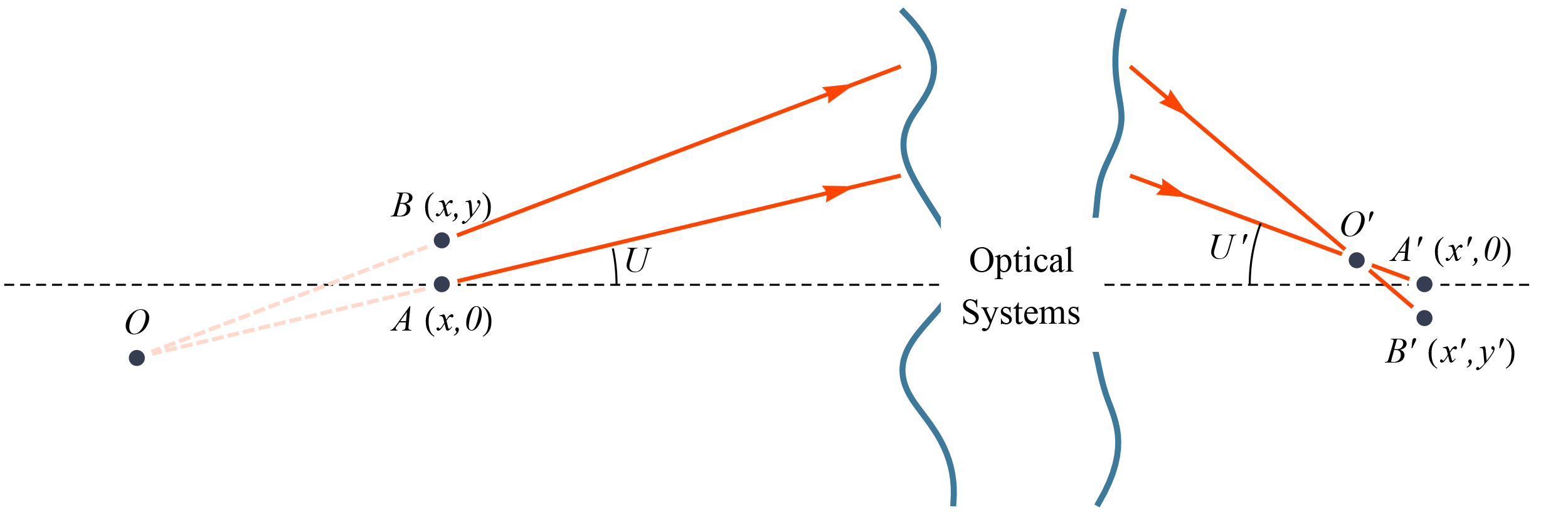

其中h=y，h'=y'，n，n'分别是介质的折射率
再利用\(h'=r_0=1.22\frac{\lambda l}{d n'}\)，注意波长变化，当恰好能分辨时，有\(h=\frac{n'\sin{u'}}{n\sin{u}}\cdot\frac{1.22\lambda l}{d n'}\)，当在镜片边缘时由于l>>d，\(\sin{u'}_{\max}=\frac{d}{2l}\)
\(\therefore h=\frac{1.22\lambda}{2n\sin{u}}\)
注意此处的\(\lambda\)指的是激发光的波长，而不是荧光的波长

令\(n\sin{u}=\mathsf{N.A.}\)为数值孔径，查表可得

知道哪个是数值孔径就行

光的偏振
布儒斯特定律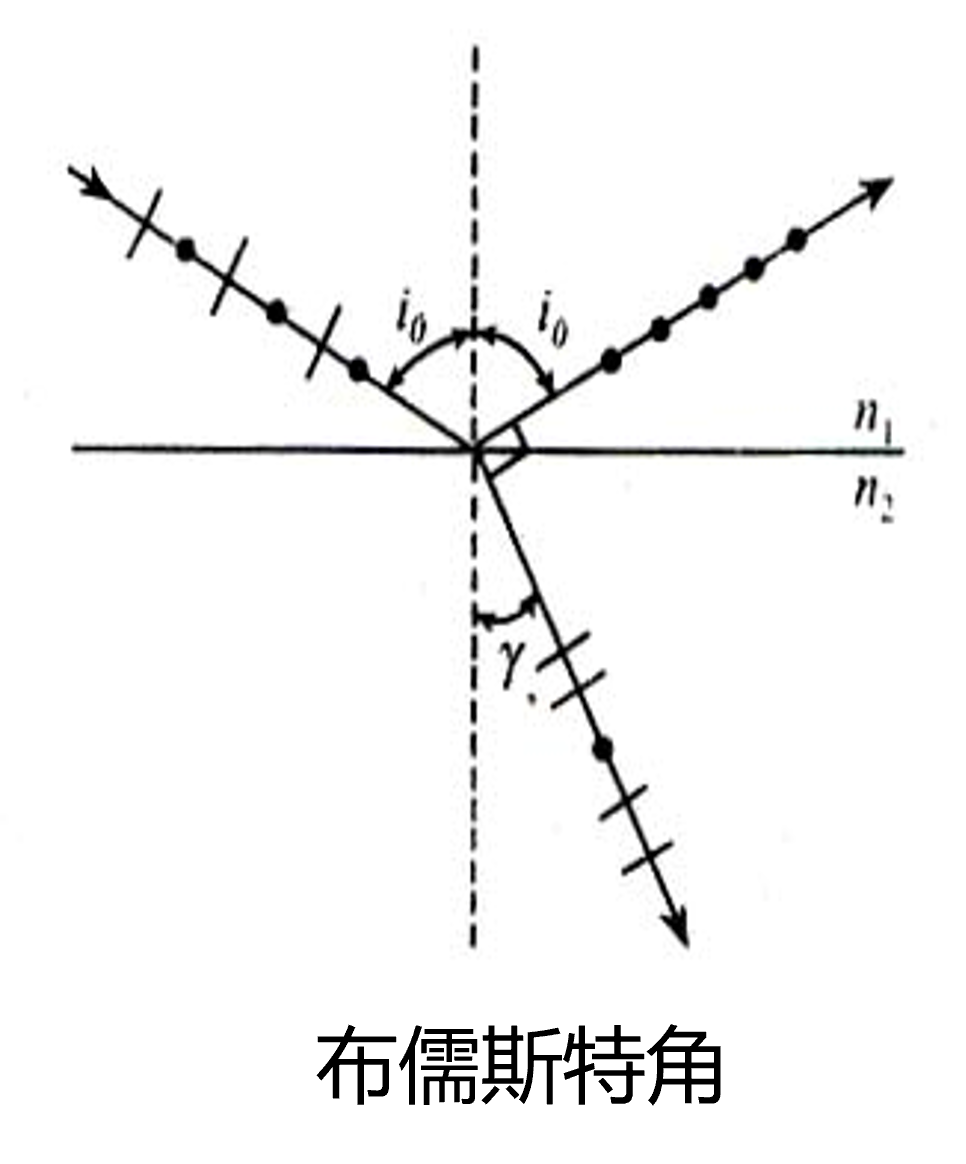

当\(i_0+\gamma=\pi/2\)时，反射光为线偏光且是s光
此时有\(n_1\sin{i_0}=n_2\sin{\gamma}=n_2\cos{i_0}\)，即\(\tan{i_0}=\frac{n_2}{n_1}\)