4 核磁共振及医学应用

学习笔记
作者: MingXiao

重点
基本原理
成像过程

4.1 基本原理

磁场中的磁矩
环形电流的磁矩\(\overrightarrow{\mu}=I\overrightarrow{S}\)，单位J/T，其中S为面积，方向与I构成右手螺旋关系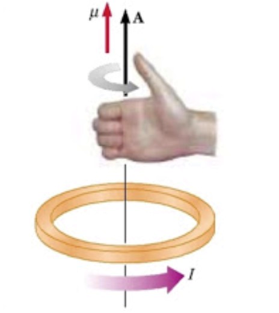

磁矩在磁场中的能量
\[E=-\overrightarrow{\mu}\cdot\overrightarrow{B_0}=-\mu B_0 \cos{\phi},\phi=\langle \overrightarrow{\mu},\overrightarrow{B_0}\rangle\]
式中\(B_0\)是外加磁场

核自旋角动量
核自旋是量子化的，有
\[P_I=\sqrt{I(I+1)}\hbar\]
其中I是核自旋量子数，有以下规律：

  1. 质子数和中子数都是偶数，I=0
  2. 质子数和中子数有一个是奇数，I是半整数（X.5）
  3. 质子数和中子数都是奇数，I是正整数

核自旋角动量的空间分量
也具有量子化的性质，有
\[P_{Iz}=m_I\hbar，m_I=I，I-1,I-2,\ldots,-I\]
\(m_I\)是自旋磁量子数，共\(2I+1\)个可能值，z方向为外磁场方向，表明\(P_{Iz}\)有\(2I+1\)个可能值

核磁矩和核自旋的关系
核磁矩用于描述自旋核在其周围空间所产生的磁场特性，有
\[\mu_I=g_N\frac{e}{2m_p}P_I\triangleq\gamma P_I\]
\[\Rightarrow\mu_I=g_N\frac{e}{2m_p}\sqrt{I(I+1)}\hbar\triangleq g_N\sqrt{I(I+1)}\mu_N\]
其中\(g_N\)是朗德因子，是常数；\(\gamma\triangleq\frac{g_Ne}{2m_P}\)是原子核的磁旋比，对于特定的核是常数；\(\mu_N=\frac{e\hbar}{2m_P}\)为核磁子，是核磁矩的最小单位

核磁矩的空间量子化
\[\mu_{Iz}=g_N\frac{e}{2m_P}P_{Iz}=g_N\frac{e}{2m_P}m_I\hbar=m_Ig_N\mu_N\]

例：下面哪些核可以用于MRI：\(^{12}C,^{18}O,^1H,^{19}F,^6Li,^{14}N\)
解：用于MRI，则其必须有核磁矩，其量子数不能是零，故前两个不行，后面都可以
最常用的是\(^1H\)，人体内含量大，灵敏度高，自旋数=1/2，只有两种取向，探测简单

宏观磁矩
本质是核磁矩从无序排列变成有序排列，磁场越强，核磁矩取向越一致，宏观磁矩越大
\[\overrightarrow{M}=\sum_{i=1}^n\overrightarrow{\mu_i}\]

塞曼效应
自旋核在磁场中的取向改变和能级分裂

相邻两级的能量差有\(\Delta E=\Delta m_Ig_N\mu_NB_0\cos{\phi}=g_N\mu_NB_0\)，即\(\Delta m_I\equiv1,\cos{\phi}\equiv1\)
由于\(^1H\)的自旋量子数\(I=\frac{1}{2}\)，仅有\(\pm \frac{g_N\mu_NB_0}{2}\)两个能级

核磁共振条件和拉莫尔公式
在外磁场中氢核磁矩受外磁场作用，会产生进动，其进动角频率为\[\omega_N=\gamma B_0\]
在频率为\(\nu\)的射频射线（RF）作用下，若有
\[h\nu=\Delta E=g_N\mu_NB_0=g_N\frac{e\hbar}{2m_P}B_0\]
\[\Rightarrow \nu = \frac{1}{2\pi}\cdot\frac{g_Ne}{2m_P}\cdot B_0=\frac{\gamma}{2\pi}B_0\Leftrightarrow\omega=\gamma B_0\]
上式称为拉莫尔公式
低能级的原子核吸收RF的能量而跃迁到高能级

α角RF脉冲
宏观磁矩\(\overrightarrow{M}\)与RF之间发生共振吸收，原先处于低能级（此时宏观磁矩与外磁场同向）的核跃迁到高能级，其磁矩方向改变，最终导致\(\overrightarrow{M}\)与\(\overrightarrow{B_0}\)的夹角会变化，如果\(\Delta \phi=\alpha\)，称该RF为α角RF脉冲
90°和180°是两个基本脉冲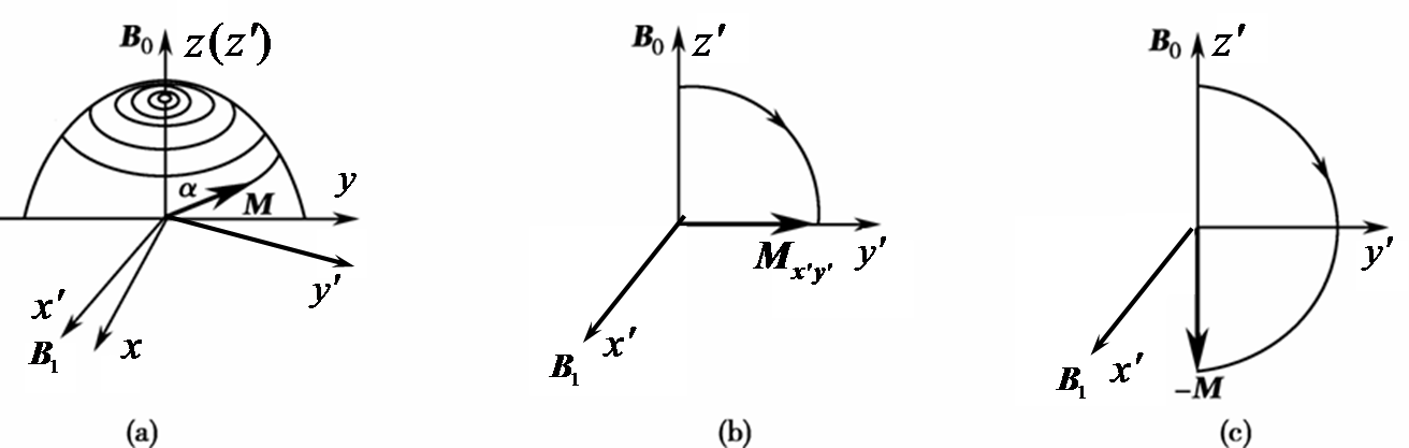

MR信号检测
大量的氢核发射和吸收能量，产生感应电场，其强度与参与共振的氢核数目和射频脉冲后的提取信号的时刻有关

弛豫过程
横向弛豫过程：
核磁矩在水平方向趋于平衡，各磁矩旋进的相位完全错乱。各磁矩在水平方向的磁性完全抵消，宏观上水平磁矩\(M_{xy}\)趋于零。是同种核之间交换能量的过程，也称自旋-自旋弛豫过程

纵向弛豫过程：
整个氢核磁矩系统恢复到未偏离磁场前的宏观磁矩（方向和大小），纵向分量\(M_z\)从小到大。是氢核和周围物质的热交换，达到热平衡，又称自旋-晶格弛豫过程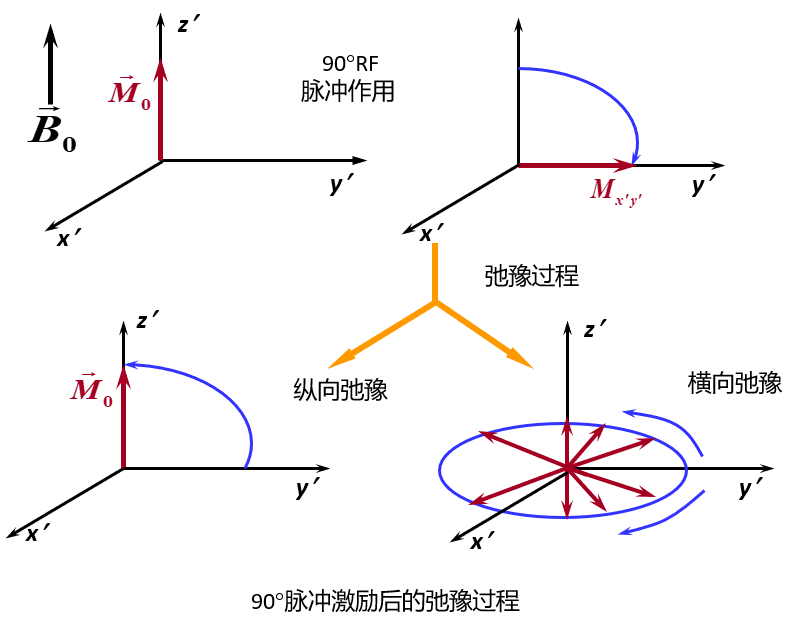

弛豫时间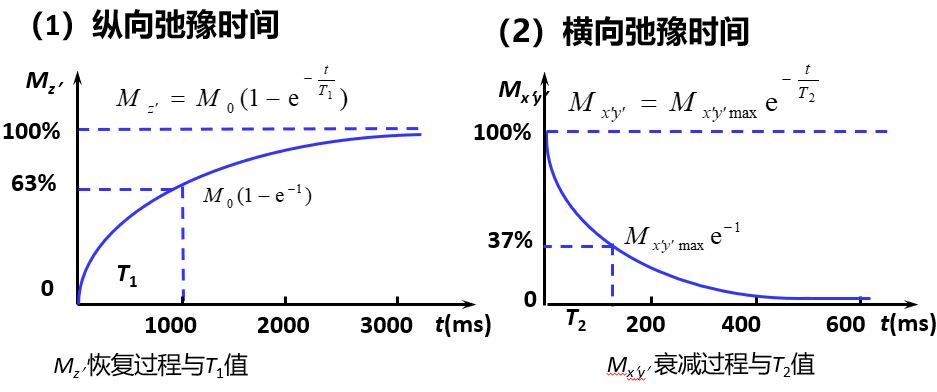

\(T_1\)是\(M_{z'}\)达到\(0.63M_0\)是的时间，\(T_2\)是\(M_{x'y'}\)减小到\(0.37M_{x'y'_{max}}\)的时间

4.2 成像过程

选择层面
外加Z方向主均匀磁场\(B_0\)，再叠加同方向的线性梯度场\(G_z\varpropto z\)，得到
\[B=B_0+zG_z\]
要使氢核跃迁，RF的频率也要随z改变，有
\[\nu=\frac{\gamma}{2\pi}(B_0+zG_z)\Leftrightarrow\omega=\gamma(B_0+zG_z)\]
不同的共振频率表示自旋核所在层面，\(G_z\)称为选片梯度场，由此完成z轴定位

选择位置
在x轴向叠加\(G_x\)编码相位，在y轴向叠加\(G_y\)编码频率，确定坐标
具体而言，在RF的照射下，向x轴向一个很小的线性梯度场，磁矩的旋进速度发生变化；停止RF照射，撤去\(G_x\)，磁矩旋进速度重新一致，但是产生了稳定的相位差，分出了x坐标
在停止脉冲的前提下，加上较大的线性梯度场\(G_y\) ，改变进动的频率，进行频率编码，接收信号时分出了y坐标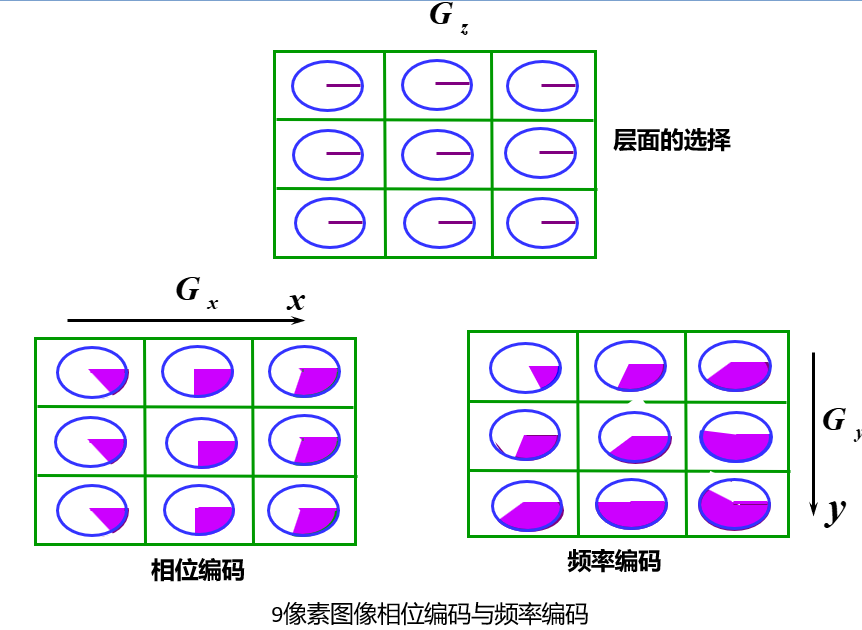

图像重建
RF照射、选片、相位编码、停止脉冲、频率编码、信号采集处理、成像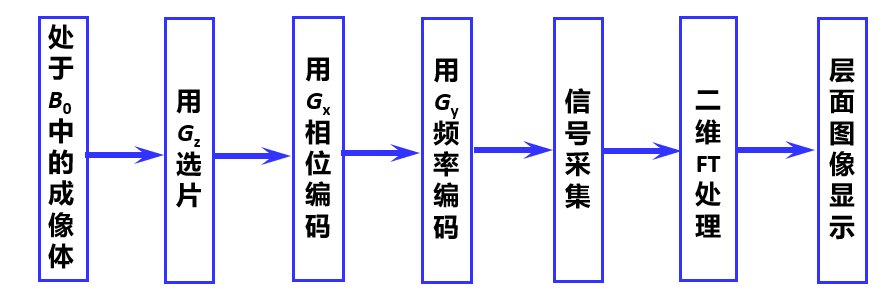

4.3 人体的磁共振成像

人体的各个组织的\(T_1,T_2\)值是不同的，可以形成\(T_1,T_2\)加权图像
各个组织的氢核密度\(\rho\)也不同，可以形成\(\rho\)加权图像

4.4 氢核密度\(\rho\)和\(T_1,T_2\)加权图像的产生

自旋-回波序列
由90°和180°RF脉冲组成，\(T_E\)是回波时间，\(T_R\)是脉冲周期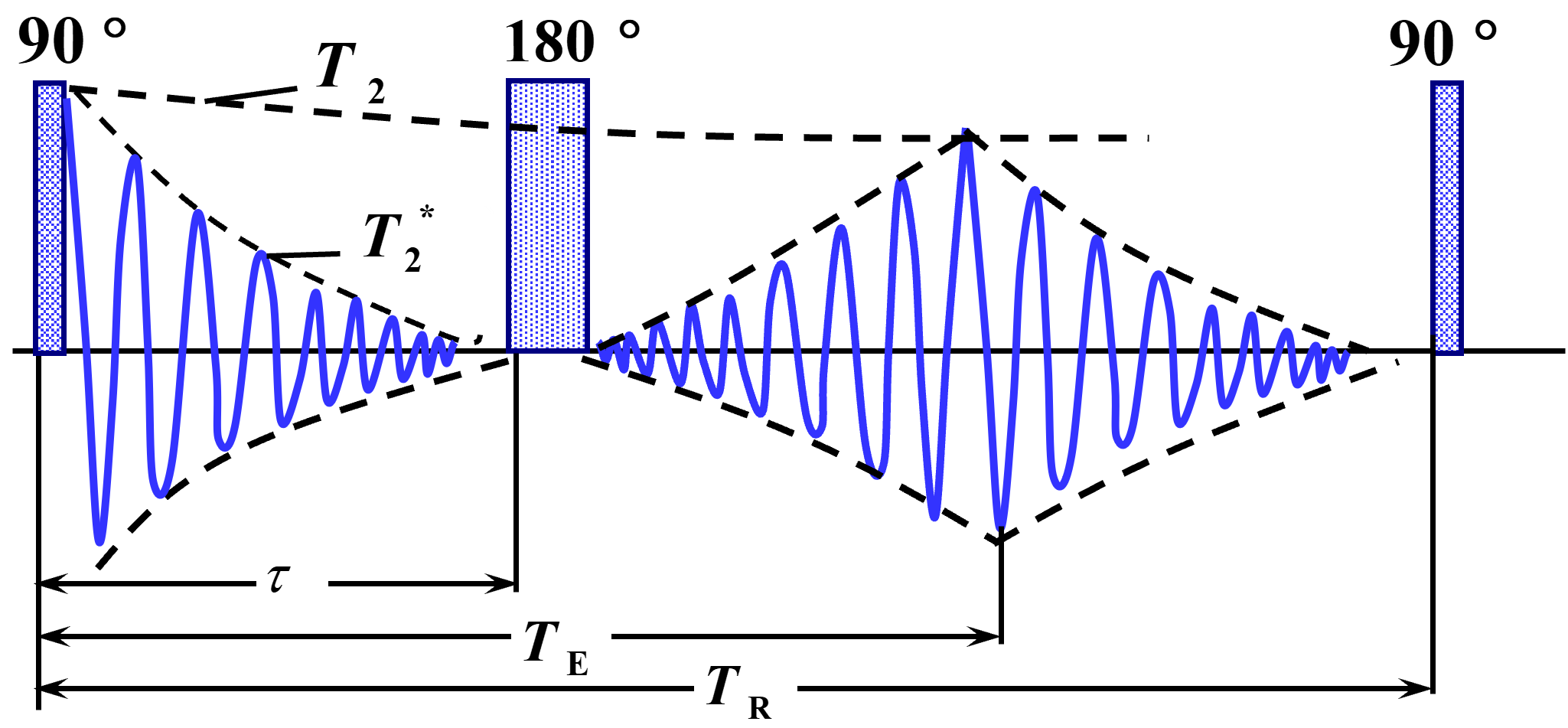

在该信号下，MR信号的幅度满足
\[A=A_0\rho(1-e^{-\frac{T_R}{T_1}})e^{-\frac{T_E}{T_2}}\]

氢核密度图像
当\(T_R>>T_1,T_E<氢核密度不同的两种组织，除开始之外，宏观磁矩大小不同，利用这种差距产生对比，得到灰度

\(T_1\)加权图像
当\(T_R\leq T_1,T_E<不同组织的\(T_1\)不同，在某一时刻得到的图像各个组织强度不同，灰度不同

\(T_2\)加权图像
当\(T_R>>T_1,T_E\geq T_2\)时，\(A=A_0\rho e^{-\frac{T_E}{T_2}}\)
注意在不同时刻采集的图像，灰度可能截然不同

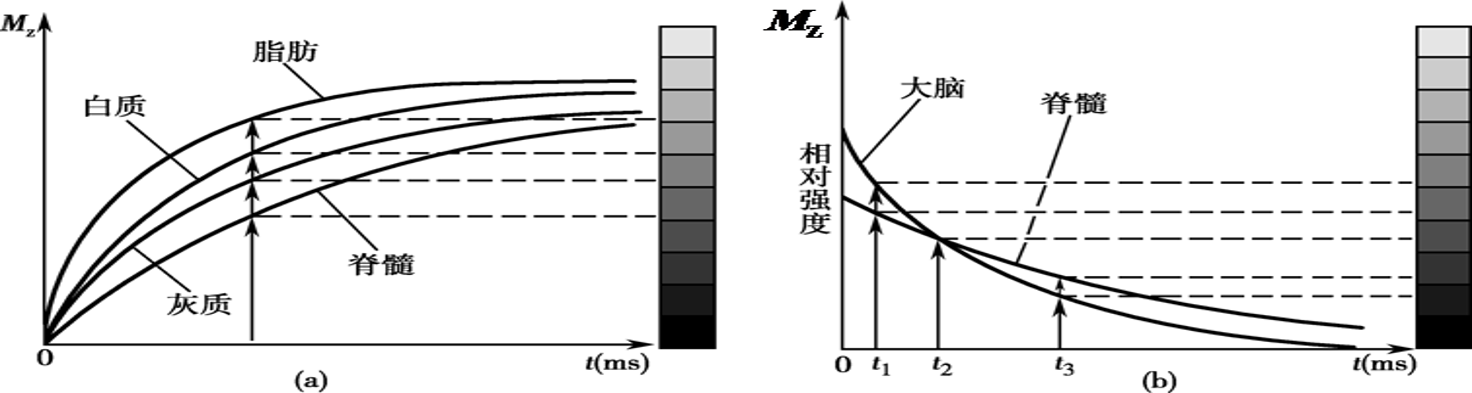
人体组织含水量差别不大（即氢核密度差不多），故后面两个的成像反差度更好

MRI造影剂
使用顺磁性物质，可以使\(T_2\)减小，在\(T_2\)加权图中含有造影剂的部分反差增大，提高分辨率

磁共振血管成像（MRA）
利用流动血液的MR信号与周围静态组织MR信号差异来建立对比度，用**时间飞跃法（TOF）和相位对比法（PC）**来重建

磁共振功能成像
两类方法

  1. 弥散成像。分子热运动导致扩散的快慢
  2. 灌注成像。流动效应，测量区域内的血容量

4.5 磁共振成像系统简介

磁场系统

  1. 静磁场
    1. 常导电磁体
    2. 永磁体
    3. 超导磁体
  2. 梯度场（实现体素编码）

射频系统

  1. 射频发生器
    1. 射频振荡器
    2. 发射门
    3. 脉冲功率放大器
    4. 脉冲程序器
  2. 射频接收器（在线圈中感应MR信号）

图像重建系统

  1. A/D转换器（便于计算机处理）
  2. 计算机（复杂的算法）
  3. D/A转换器（按灰度显示）
  4. 图像显示器


Comments