2 原子核及放射性
重点:
原子核基本性质,衰变类型原子核衰变规律和应用
射线与物质作用的几种形式
2.1 原子核组成
原子核由质子和中子组成,二者统称核子
原子核质量用u表示,\(1u=\frac{1}{12}m(_6^{12}C)\),用其来度量质量时,数值接近原子核核子数A
核素:确定的质子数、核子数和能量状态的中性原子,用符号表示为\(_Z^AX_N\),其中Z为原子序数,A为核子数
同位素:Z相等,A不相等
同质异能素:Z、A都相等,但是能级不同
原子核大小
由经验公式\(R=R_0A^{\frac{1}{3}}\)可以得到,\(R_0=1.2\times10^{-15}\),原子核密度\(\rho=\frac{3u}{4\pi R_0^3}\approx=10^{17}kg/m^3\)
2.2 原子核的结合能及质量亏损
质量亏损: 原子的结合能: 比结合能: 原子核衰变 α衰变 β衰变 \(\beta^-\)型 \(\beta^+\)型 电子俘获型 γ衰变 衰变规律 半衰期\(T\) 生物半衰期\(T_b\) 有效半衰期\(T_e\) 平均寿命\(\tau\) 放射性活度 例:求5g铀盐(\(U_3O_8\))的放射性活度,已知\(T_U=4.47\times10^9 a\) 放射性平衡 当子核的A与母核相近并达到最大值时,称为放射性平衡(对\(N_B\)求导) 例:对\(A\overset{\lambda_A}{\rightarrow}B\overset{\lambda_B}{\rightarrow}C\),问(1)子核何时达到最大(2)一次洗脱子核,再经过多久再次洗脱,得到的产物最多 激发与电离 散射和韧致辐射 射程 正电子与物质相互作用 电离比值 α粒子 β粒子 射程和吸收规律
设原子核\(_Z^AX\)质量\(m_d\),实验表明,\(m_d
自由核子结合为原子核需要释放的能量,有
\[\Delta E=\Delta m\mathcal{C}^2\]
1u对应931.5MeV的能量
\[\varepsilon=\frac{\Delta E}{A}\]
这个值越大,核子结合得越紧密,越稳定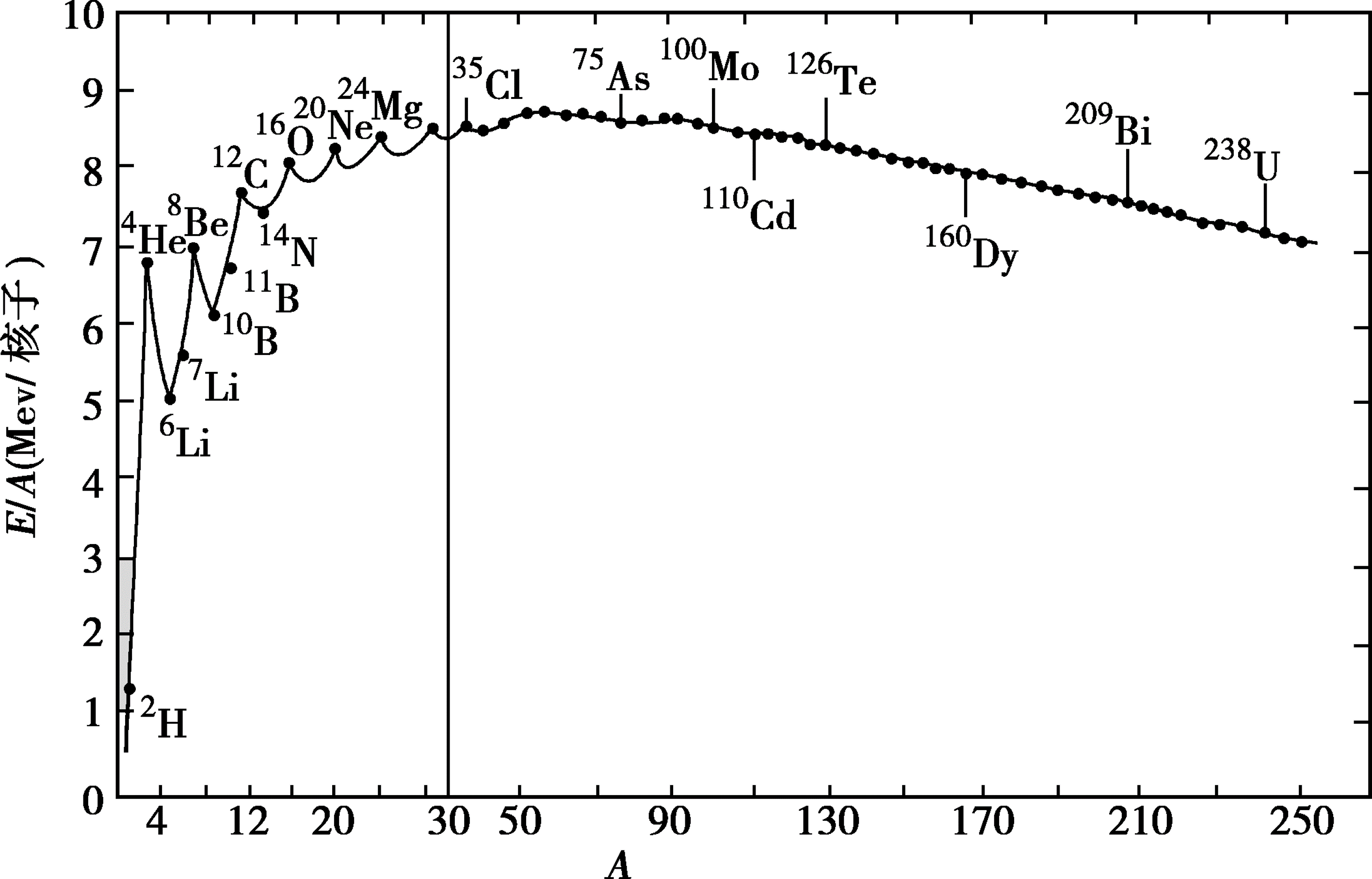
可见轻核和重核的比结合能小,所以用轻核聚变和重核裂变的方法2.3 原子核的衰变方式及规律
自发放出射线,变为另一种核素
\[_Z^AX\rightarrow _{Z-2}^{A-4}Y+ _2^4He+Q\]
α粒子就是氦核,发生的前提是A>209,Q是能量
特点:
分为\(\beta^-\)、\(\beta^+\)和电子俘获型,由于有中微子参与,能量将任意分配,所以射线谱是连续的
\[_Z^AX\rightarrow _{Z+1}^AY+e^-+\overline{\nu_e}+Q\]
β射线是电子流,\(\overline{\nu_e}\)是反中微子
特点
\[_Z^AX\rightarrow _{Z-1}^AY+e^++\nu_e+Q\]
由于电子湮灭\(e^++e^-\rightarrow 2\gamma+Q\),两个光子相向,能量为0.511MeV,\(\beta^+\)粒子射程仅1-2mm
母核俘获一个核外电子而变成子核,并放出中微子
\[_Z^AX+e^-\rightarrow _{Z-1}^AY+\nu_e+Q\]
就是原子核跃迁
特点
在dt内发生衰变的原子核数目-dN正比于当前存在的原子核数目N和dt,即
\[-dN=\lambda Ndt \Rightarrow N=N_0\mathcal{e}^{-\lambda t}\]
\(\lambda\)是衰变常量,\(N_0\)是初始原子核数
又称物理半衰期,由上式可得,当\(N=N_0/2\)时,解得\(T=\frac{\ln{2}}{\lambda}=\frac{0.693}{\lambda}\)
可以用半衰期来表示N,即\(N=N_0(\frac{1}{2})^{\frac{t}{T}}\)
由于各种代谢作用,生物体排除放射性核素的规律
同时考虑半衰期和生物半衰期,有
\[\frac{1}{T_e}=\frac{1}{T}+\frac{1}{T_b}\]
衰变定律改写为
\[N=N_0\mathcal{e}^{-(\lambda_b+\lambda)t}\]
其中\(\lambda_e=\lambda+\lambda_b\),分别是有效、衰变、生物衰变常数
放射性核素平均生存时间,下面是计算方法
即将衰变的dN个核,设其生存了t,则这dN个核的寿命之和有\(t(-dN)=t\lambda Ndt\)
带入N的表达式,得到所有的核寿命之和\(\sum=\int_0^\infty \lambda Nt\,dt=\frac{N_0}{\lambda}\)
所以\(\tau=\frac{\sum}{N_0}=\lambda^{-1}=\frac{T}{\ln{2}}=1.44T\)
单位时间内发生衰变的原子核数,记为A,单位为Bq,1Bq=1次衰变/s
\[\therefore A=-\frac{dN}{dt}=\frac{\lambda Ndt}{dt}=\lambda N=\lambda N_0 \mathcal{e}^{-\lambda t}=A_0\mathcal{e}^{-\lambda t}\]
实际上\(A_0=N_0\lambda\)
解:由\(A=\lambda N\)可知要求\(\lambda\)和\(N\),\(N=N_A \frac{5g}{238g/mol}\),\(\lambda=\frac{ln{2}}{T_U}\)
注意\(\lambda\)单位是/s,\(T_U\)单位是年,\(N_A=6.02\times10^{23}\),换算后解得A
许多核素不止衰变一次,称为级联衰变
\[A\overset{\lambda_A}{\rightarrow}B\overset{\lambda_B}{\rightarrow}C\]
在这个反应中,\(N_A=N_{A_0} \mathcal{e}^{-\lambda_At}\),但在考虑B时,要考虑B和C的反应,有
\[dN_B=N_A\lambda_Adt-N_B\lambda_Bdt\]
结合上面二式,有
\[\therefore N_B=\frac{N_{A_0}\lambda_A}{\lambda_B-\lambda_A}(\mathcal{e}^{-\lambda_A t}-\mathcal{e}^{-\lambda_B t})\]
当\(t\rightarrow \infty\)时,有
\[N_B\approx N_A\frac{\lambda_A}{\lambda_B-\lambda_A}\approx N_A\frac{\lambda_A}{\lambda_B}\]
此时将子核分离,又会重新平衡
用这种方法可以由长寿命核素制取短寿命核素,装置为核素发生器
如果母核半衰期远小于子核,那么一段时间后,母核几乎全部转化为子核,之后子核按自己的方式衰变
解:(1)就是对\(N_B\)求导
(2)有第一题得到\(t_1\),代入\(N_A=N_{A_0} \mathcal{e}^{-\lambda_At}\)得到\(N_{A_0}^{'}\),将\(N_{A_0}^{'}\)替换\(N_B\)中的\(N_{A_0}\),再次求导2.4 射线与物质的相互作用
激发:射线使原子电子跃迁
电离:电子跃迁出原子
散射:射线受原子静电场作用而改变方向
韧致辐射:见上方
射线在物质中运动的路程沿入射方向的投影
就是湮灭
射线使物质每厘米路径上产生的离子对,表示对机体的损伤程度 ,与质量,带电量,速度正相关
质量大,速度慢,带电量多
质量小,受多次散射速度下降快,会发生韧致辐射
β射线的能量越高速度越快,但是电离比却越小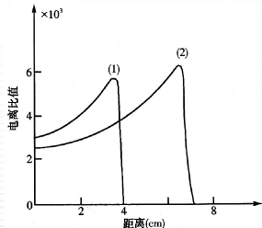
图中1为β,2为α
α粒子:电离比大,射程短,在生物体内仅几百微米
β粒子:电离比小,射程长,比α大100多倍;在外照射下危害大