1. X射线及医学应用
重点:
X射线的产生
X-CT的成像原理
X射线是一种高频、短波的电磁波
波长:\(10-10^{-3}\)nm,介于紫外线和\(\gamma\)射线之间
频率:\(3\times10^{16}-3\times10^{20}Hz\),约为可见光103倍
1.1 X射线的产生
一般方法:高速运动的电子受阻会辐射X射线
产生条件:电子源、标靶、加速电场、高度真空
产生装置:X射线管
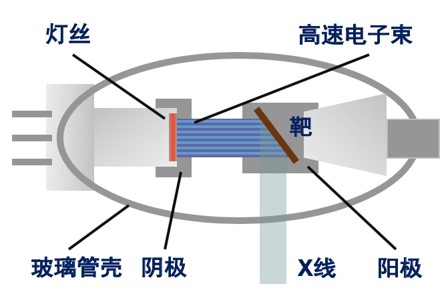
注意各个装置
实际焦点是电子流在靶面上的撞击面积(与大小和灯丝的形状有关)
实际焦点的投影面积为有效焦点
由于电子能量大部分发热,为了降低靶面温度,多采用旋转阳极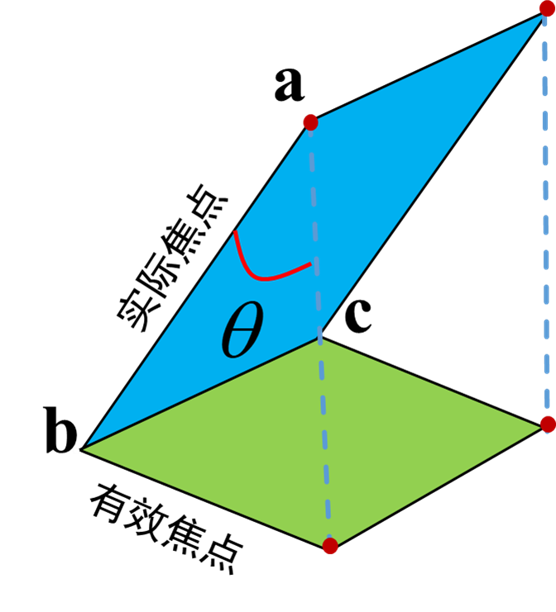
1.2 X射线的性质
X射线的强度
def:能流密度(S) 单位:\(W·m^{-2}\)
\[I=\sum\limits_{i}{N_i\mathcal{h}\nu_i}=N_1\mathcal{h}\nu_1+N_2\mathcal{h}\nu_2+\ldots+N_n\mathcal{h}\nu_n\]
\(N_i\)表示能量为\(\mathcal{h}\nu_i\)的光子数目
调节强度
调节管电流,即调节N
调节管电压,即调节\(\nu\)
X射线的硬度
\(\nu\)越大,能量越大,贯穿本领越大,X射线越硬
调节管电压可调节硬度
X射线谱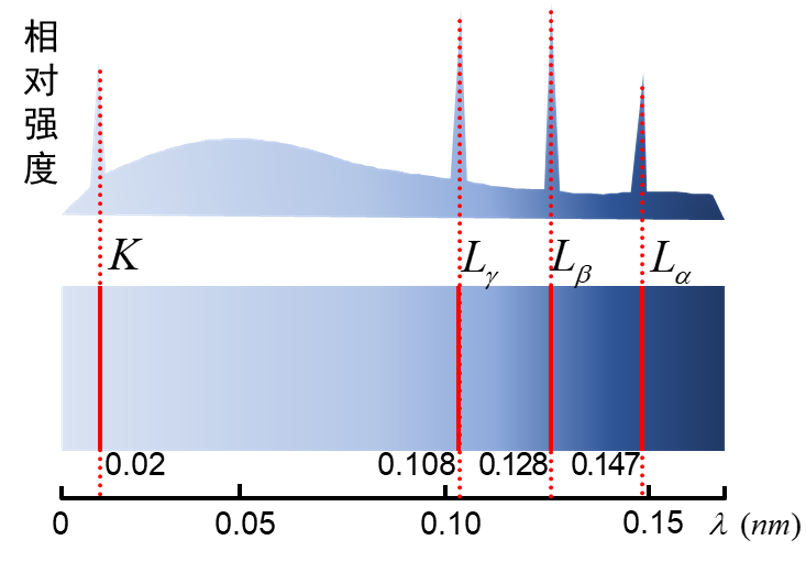
连续谱产生机制:电子受靶面制动,动能转化为光子辐射出去,称韧致辐射
由于随机性,宏观上产生了连续的谱线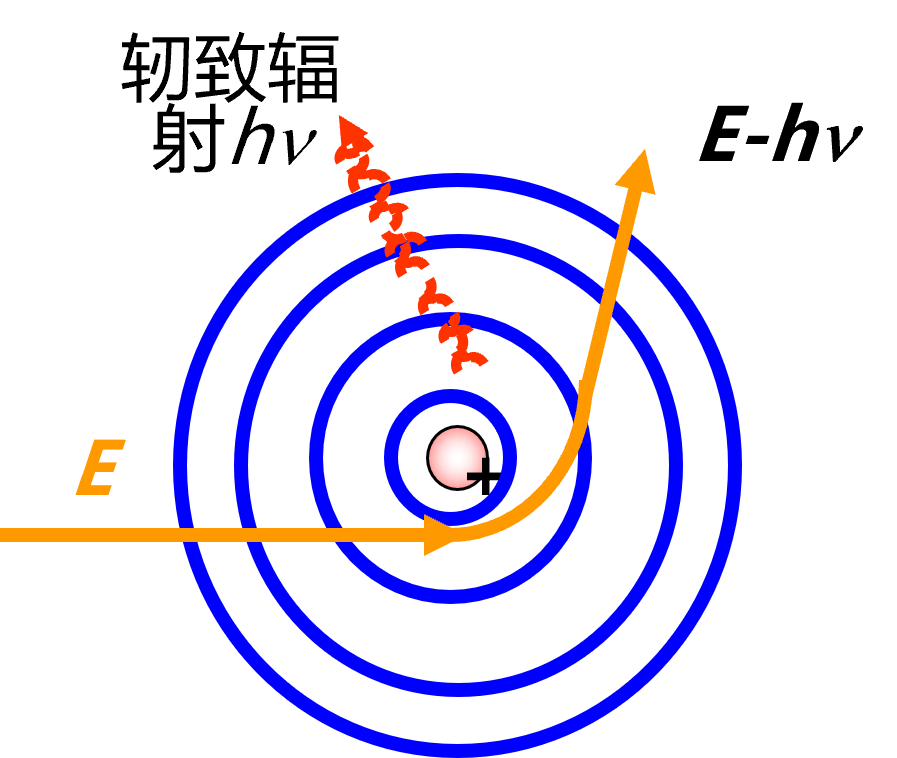
连续谱特征
\[E=\mathcal{h}\nu=\mathcal{h}\frac{\mathcal{c}}{\lambda}\]
\(E_{\max}\)就是当电子动能全部转化为辐射能,即\(E_{\max}=\mathcal{e}U\)
\[\therefore \lambda_{\min}=\frac{\mathcal{hc}}{\mathcal{e}U}\]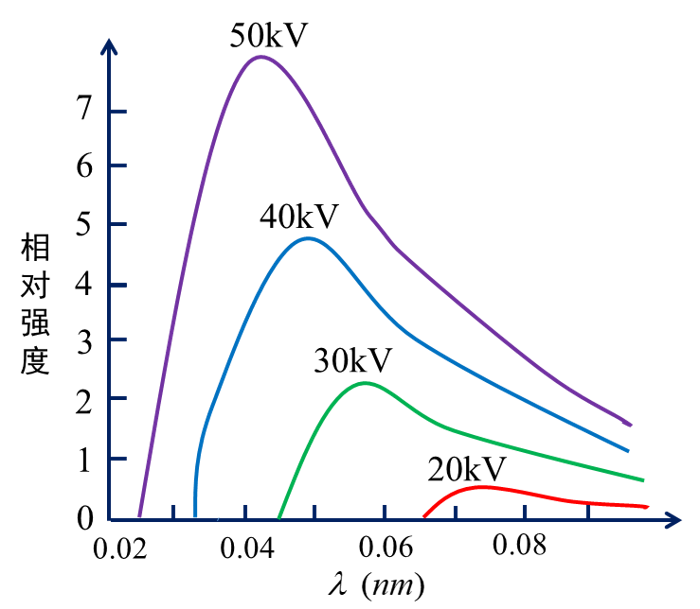
管电压上升,\(\lambda_{\min}\)变短;管电流上升,辐射强度变大
标识谱线的产生
各能级电子跃迁到内壳层得到空位,发出的光子频率高,波长短
但是,医用X射线的能量主要集中于连续谱中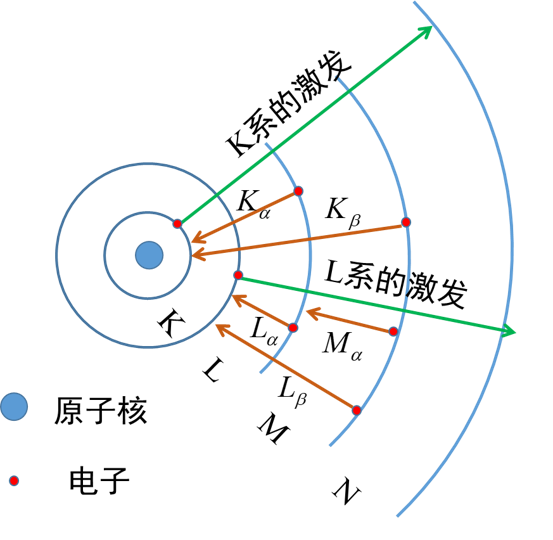
不同物质,尖峰位置和分布不同;同一物质尖峰位置不随电压变化
标识谱取决于阳极靶材料,可用于光谱分析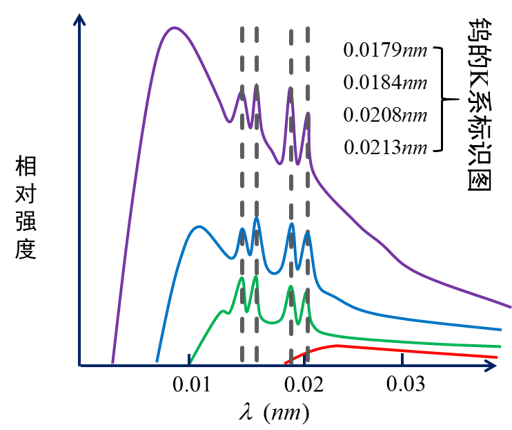
其他性质
电离作用:X射线穿过物质时使之电离,是生物效应的基础
荧光作用:打在某些物质上可以产生荧光,是传统X射线透射的基础
生物效应:引起生物组织的多种反应,放射治疗和辐射防治的基础
贯穿效应:用于X射线透射成像
光化学效应
1.3 物质对X射线的衰减规律
单色X射线的衰减规律
设\(I_0\)为入射强度,\(I\)为透射强度,\(\mu\)为衰减系数,则有
\[I=I_0\mathcal{e}^{-\mu x}\]
\(x\)为透射距离
临床上常用质量吸收系数\(\mu_m\)和质量厚度\(x_m\),以消除密度的影响
\[\mu_m=\frac{\mu}{\rho}\]
\[x_m=x\rho\]
\[\therefore I=I_0\mathcal{e}^{-\mu_m x_m}\]
物质由液、固态转变为气态时,密度变化很大,但\(\mu_m\)值不变。
\(\mu_m\)值可以用来在物质之间比较对X射线的吸收本领
单元素的质量衰减系数
\[\mu_m=kZ^\alpha\lambda^{3}\]
Z为吸收物质的原子系数,\(\lambda\)为X射线波长
指数α一般取3-4,与吸收物质和射线波长有关
多种元素混合物质的质量衰减系数
各元素的\(\mu_m\)按照所含质量比例计算的平均值
吸收物质为水、空气和人体组织时,对于医学上常用的X射线,指数α可取3.5
若是骨骼,则α更大,图像上有明显区别
1.4 X射线在医学诊断中的应用
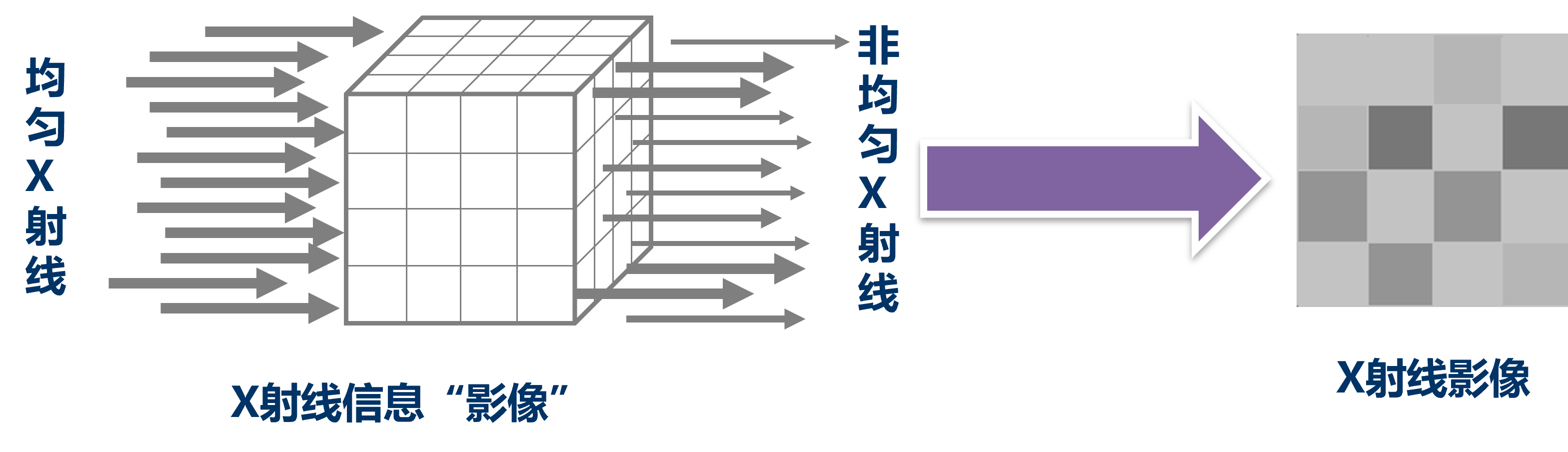
造影剂
可以提高对比度
数字减影血管造影(DSA)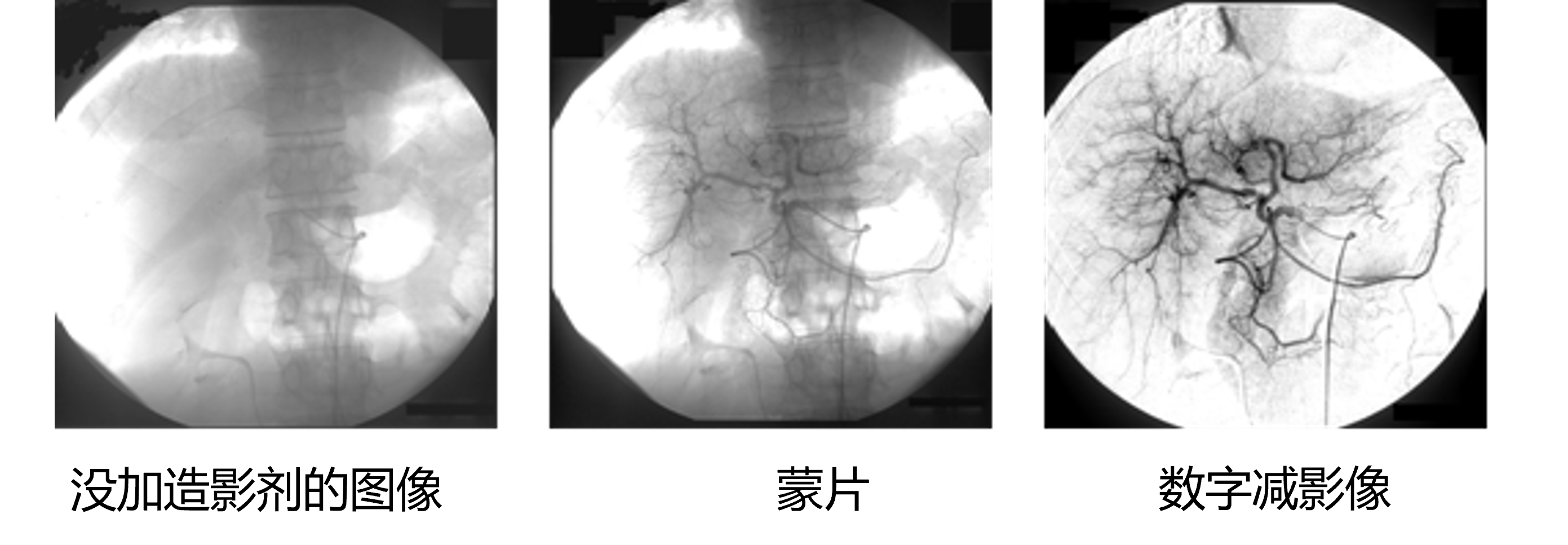
X-CT:X射线管环绕人体某一层面扫描
X-CT基本原理
将欲观测层面分解为\(n\times n\)个体素的矩阵阵列,求解各个体素的\(\mu\)值来重建图像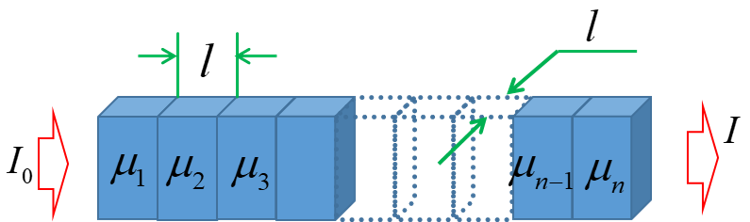
对于上图,将不均匀介质分成若干体素,有
\[I_1=I_0\mathcal{e}^{-\mu_1 l}\]
\[I_2=I_1\mathcal{e}^{-\mu_2 l}=I_0\mathcal{e}^{-(\mu_1+\mu_2) l}\]
\[I_n=I_0\mathcal{e}^{-l\cdot\sum\limits_{i}\mu_i}\]
\[\therefore \mu_1+\mu_2+\ldots+\mu_n=\frac{1}{l}\ln{\frac{I_0}{I_n}}\]
图像重建的数学方法
以下方矩阵为例
\[
\begin{bmatrix}
\mu_{11}&\mu_{12}\\
\mu_{21}&\mu_{22}\\
\end{bmatrix}
\]
在水平方向和竖直方向透射X射线,假定得到
\[p_1=\mu_{11}+\mu_{12}=8\]
\[p_2=\mu_{21}+\mu_{22}=9\]
\[p_3=\mu_{11}+\mu_{21}=10\]
\[p_4=\mu_{12}+\mu_{22}=7\]
注意,上式只有三条独立方程,需要再取一条左对角线的投影
\[p_5=\mu_{11}+\mu_{22}=5\]
解得
\[
\begin{bmatrix}
\mu_{11}&\mu_{12}\\
\mu_{21}&\mu_{22}\\
\end{bmatrix}
=
\begin{bmatrix}
3&5\\
7&2\\
\end{bmatrix}
\]
目前临床使用的X-CT机采用1024×1024等矩阵
获取待测介质体素\(\mu\)值
用下图坐标系,绕原点小角度转动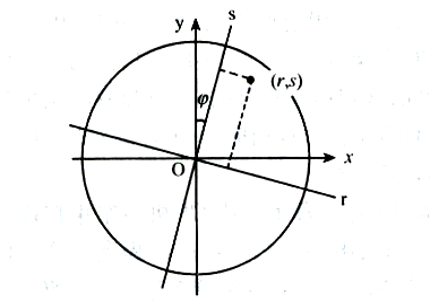
\[p(\mu,\phi)=\int_{r,\phi}\mu(x,y)\,ds\]
重建图像的关键
快速多方向测量投影
快速求解\(\mu(x,y)\)
X-CT简介
第一代:单束扫描,射线管和探测器同步平移和旋转,扫描时间长,成像速度慢
第二代:窄角扇束扫描,射线管和探测器只有旋转,扫描速度快
第三代:广角扇束扫描,射线管和探测器只有旋转,扫描速度快
第四代:锥形束多排螺旋扫描,非常快
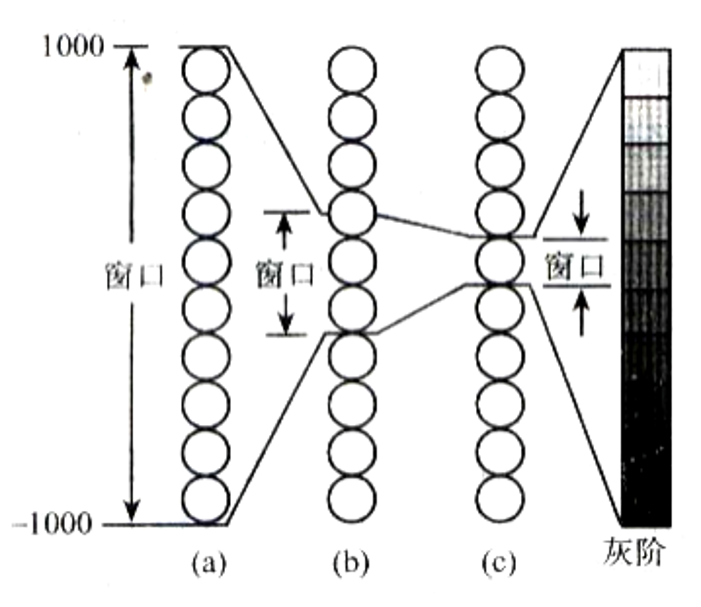
CT值和窗口技术
X-CT图像由不同灰度的小方块(像素)排列,灰度由CT值决定,有
\[CT_值=K(\frac{\mu_待-\mu_水}{\mu_水})\]
由于人眼只能分辨16灰度,就有了窗口技术:将感兴趣的部位对比度增强,使CT值差别小的组织能分辨