1 序列比对
目的:根据序列之间的功能或演化关系,有效地检测序列之间的相似性
1.1 序列比对评价
序列比对后得到的结果是匹配分数和匹配序列
匹配序列如下
\[
MV-SA\\
|\,\,|\,\,\,\,\,\,\,\,\,\,:\,\,\,.\\
MVHTE
\]
其中"\(|\)"表示两个序列identical," "表示一方是空白的,"\(:\)"表示二者similar,"\(.\)"表示not similar
这些符号由替换矩阵决定,替换矩阵规定了每个残基和其他残基匹配时的分数
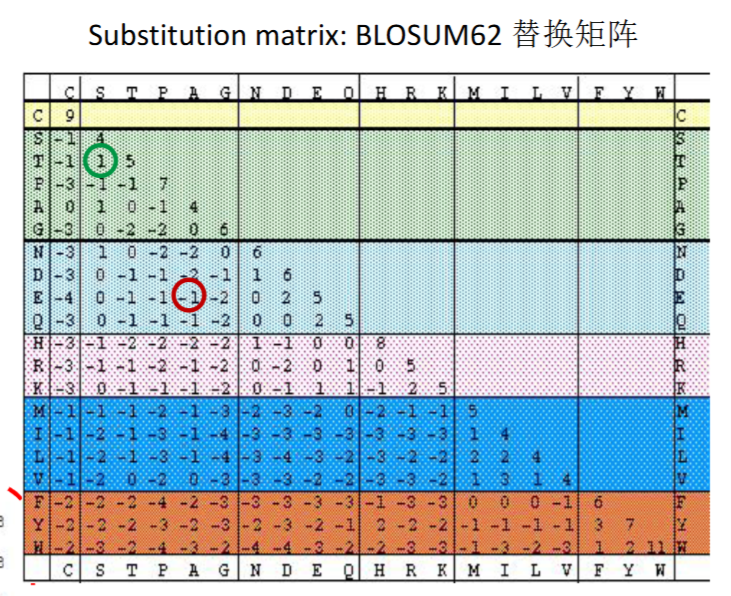
当存在空白时,认为是发生了indel(insertion/deletion),即一条序列的插入就是另一条序列的删除
空白会带来惩罚,惩罚规则如下
- opening:第一个空位,penalty = d
- extending:后续的空位扩展,penalty = e
- 一般而言\(e
- Penalty = d + (n-1)*e
最终两条序列的匹配总分为
\[
\mathsf{Score} = \sum \mathsf{Substitution\, Scores} -\sum\mathsf{Gap\, Penalty}
\]
1.2 全局比对和动态规划
1.2.1 全局比对
全局比对:将输入序列的所有残基排列起来,根据评价规则求出最大的得分,即最优比对结果
全局比对的思想:最好的比对 = 前一个最好的比对 + 这个位置的最好比对
也就是动态规划而非贪心,因为前一项不是\(\sum\)局部最优
1.2.2 动态规划
Dynamic Programming(DP),写为公式就是
对于\(X,Y\)两条序列
\[
F(i,j) = \max \begin{cases}
F(i-1,j-1) + s(x_i,y_j)\,\,, x_i 与y_j配对 \\
F(i-1,j) + d\,\,\,,\,\,\,x的第i位是gap\\
F(i,j-1) + d\,\,\,,\,\,\,y的第j位是gap\\
\end{cases}
\]
其中\(F(i,j)\)是这个序列匹配到\((i,j)\)位置时的分数,\(s(x_i,y_j)\)是\(x_i,y_j\)匹配时的分数,\(d\)是gap penalty
表示为图像就是
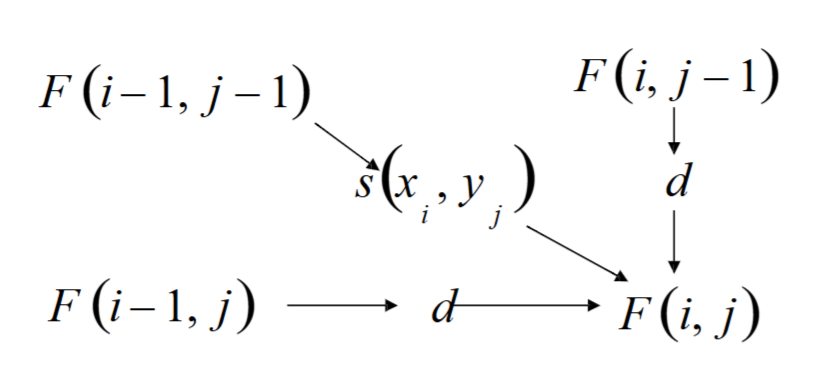
一共有三条路通向下一个,目标是找到能使\(F(i,j)\)最大的,因此,可以用填空的方式求解
例:假定碱基的空白惩罚为-5,替换矩阵为
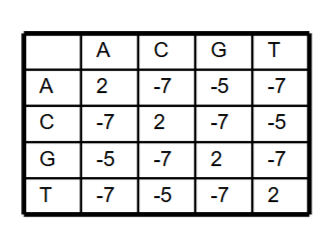
配对序列"AAG"和"AGC"
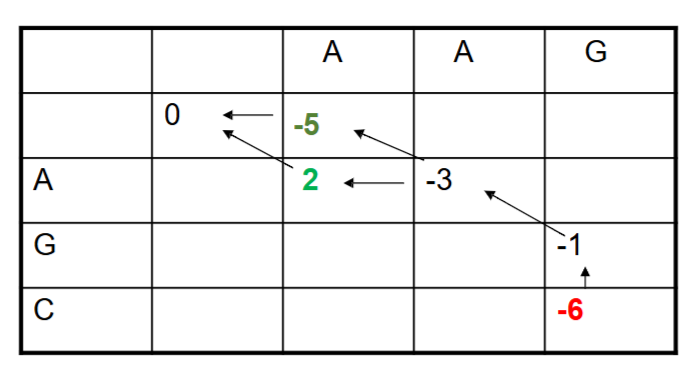
解:画出这两个序列的表格,其中空白表示gap,箭头表示延伸方向,结果为
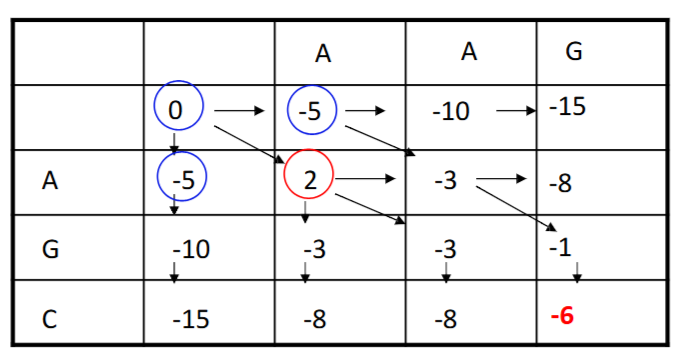
那么就有两条路进行选择:\(AAG-\\A-GC\) 和 \(AAG-\\-AGC\) ; 前者是0,2,-3,-1,-6,后者是0,-5,-3,-1,-6
在画表格时,先计算水平和竖直两个方向会简化计算
在得到最终结果后进行回溯,可以得到序列
1.2.3 从全局到局部
全局比对是在全局范围内的最优数学解,但是这个算法忽略了生物学上的问题,即
- 所有片段的重要性不尽相同
- 占基因很大的内含子不表达,比对这一部分无意义
因此,使用优化后的局部比对算法,公式为
\[
F(i,j) = \max \begin{cases}
F(i-1,j-1) + s(x_i,y_j)\,\,, x_i 与y_j配对 \\
F(i-1,j) + d\,\,\,,\,\,\,x的第i位是gap\\
F(i,j-1) + d\,\,\,,\,\,\,y的第j位是gap\\
0 \,\,\,\,,\,\,\,\,\mathsf{BeginAgain}
\end{cases}
\]
即当某一步出现了负值时,将其认为新的序列的开始,效果上,就是
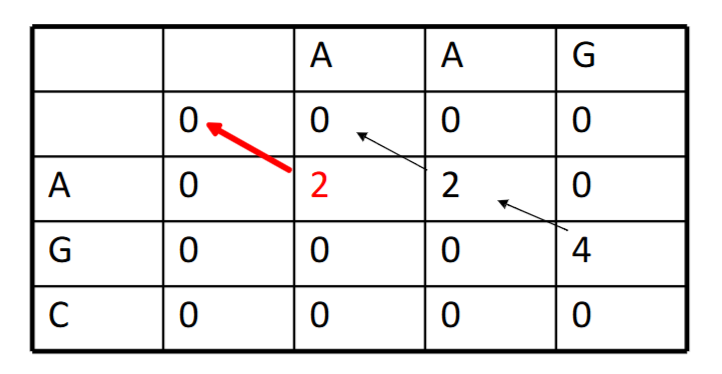
最优序列是:\(AG\\AG\) ; 次优序列是:\(A\\A\)
与全局比对相比,局部比对的效果更能反映生物学关系

1.2.4 BLAST
将一个DNA片段在基因库中进行比对时,如果总是指向上面的DP算法,将会非常耗时
可以预见,匹配的基因只会出现在表格的主对角线附近,那么只需要在网格的主对角线两侧有限区域内进行评分,将大大减少时间而不减少准确度
1.3 马尔可夫模型
马尔可夫模型用来模拟伪随机变化的系统
1.3.1 马尔可夫模型
以天气变化为例,下面是天气变化的马尔科夫链
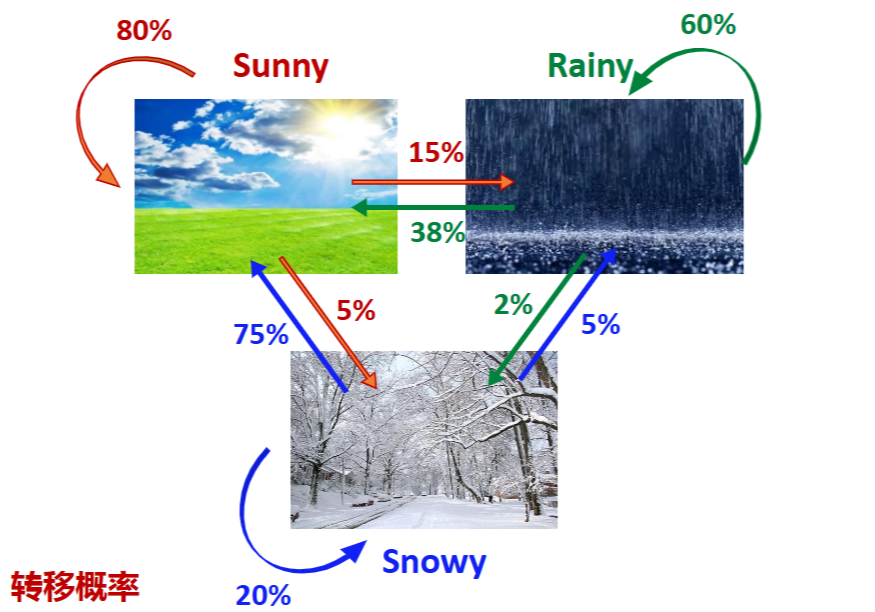
概率都是条件概率,那么可以写出状态转移概率矩阵和初始概率分布

\[ \pi =(0.7, 0.25, 0.05) \]
注意每一行之和都是1,而每一列不一定
下面给出定义:
马尔可夫链描述一个连续的离散随机过程,即一种状态的序列的变化
\[
\{q_1,q_2,\ldots,q_k\}
\]
其中\(q_i\)一定属于状态
\[
\{S_1, S_2,\ldots,S_n\}
\]
中的某一个,状态之间的转移概率
\[
a_{ij} = P(q_t=S_j| q_{t-1}=S_i)
\]
构成的矩阵就是状态转移概率矩阵,显然这不是对称阵
给定的初始概率分布记为
\[
\pi = P[q_0 = S_i]
\]
对于天气变化序列

给出概率,为
\[
P(O) = 0.7 * 0.15 * 0.6 * 0.6 * 0.02 * 0.2
\]
1.3.2 在序列比对中的作用
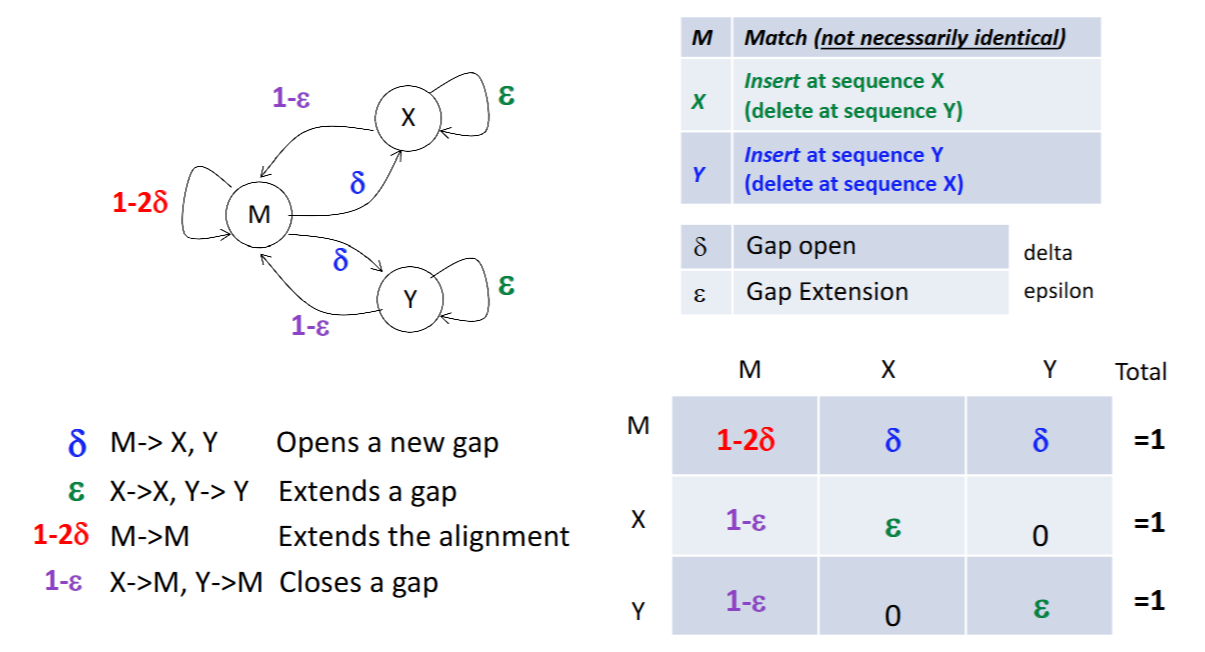
假定序列比对存在以下状态
- M:Match,即配对,不必须identical
- X:在X链发生了一次插入,即X链的A配对了Y链的Gap
- Y:相反,在Y链的B配对了X链的Gap
给出马尔科夫链
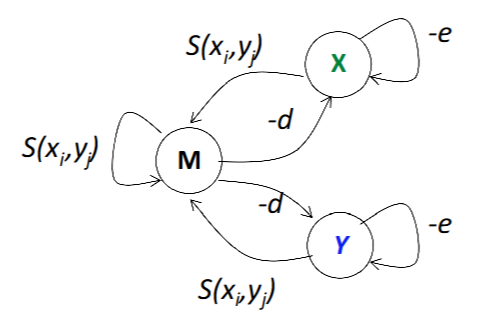
为什么X与Y之间没有转移?
在序列对比中,形如\(A-\\-B\)的配对是不允许的,即Gap Closing一定会到Match,而不会在对面新开一个
根据惩罚给出发生的概率
1.3.3 隐马尔可夫模型
状态路径无法预测,但是有观测结果可以反映状态变化
隐马尔科夫模型可以解决三大问题
- 评估:计算在给定模型下观测序列出现的概率,反推最可能的过程
- 模型学习
- 解码/预测问题
以天气为例,首先知道天气的状态转移概率矩阵和初始状态概率,也知道天气对人的穿着的影响的生成概率矩阵
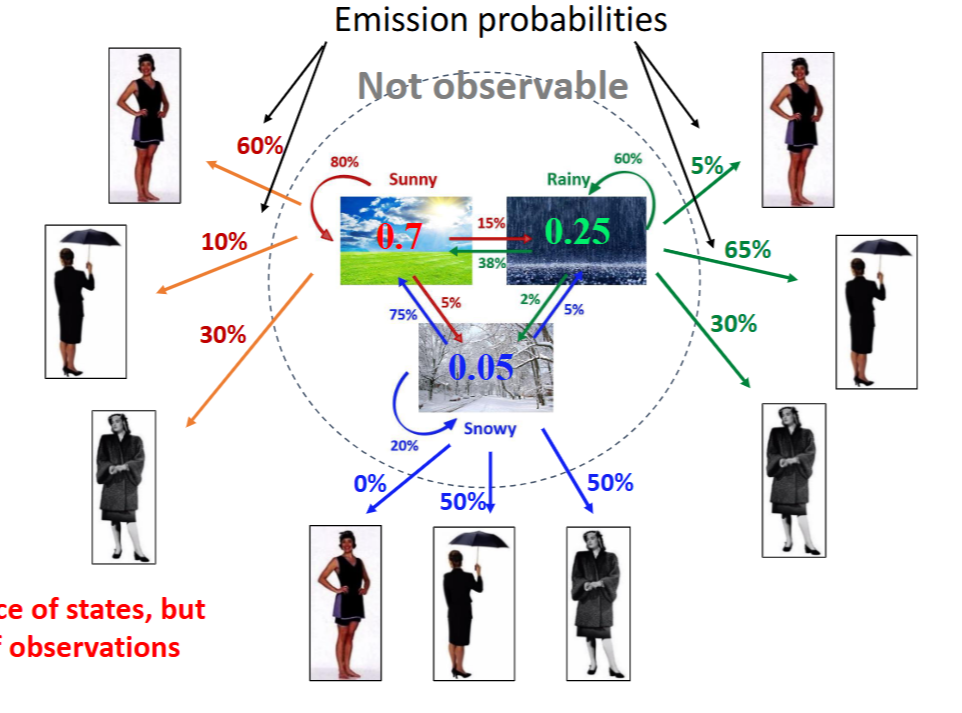

给定一组观测结果:coat,coat,umbrella,umbrella,bathing suit,umbrella,umbrella
那么根据全概率公式和贝叶斯公式,有
\[
P(O) = \sum P(O|Q_i)P(Q_i) = \sum P(O|q_1,q_2,\ldots,q_k)P(q_1,q_2,\ldots,q_k)\\
=\Pi P(o_i|q_1,q_2,\ldots,q_k)P(q_1,q_2,\ldots,q_k)
\]
在这组观测结果下,当条件为全晴天时的概率为
\[
P(O|q_1\sim q_7 =sunny)P(q_1\sim q_7) = (0.7*0.8^6)*(0.3*0.3*0.1*0.1*0.6*0.1*0.1)
\]
当然,使用前提后一天状态仅受前一天影响
1.3.4 隐马尔科夫预测模型
使用隐马尔科夫模型来预测一段基因序列是否为编码区/非编码区,给出转移概率矩阵和生成概率矩阵
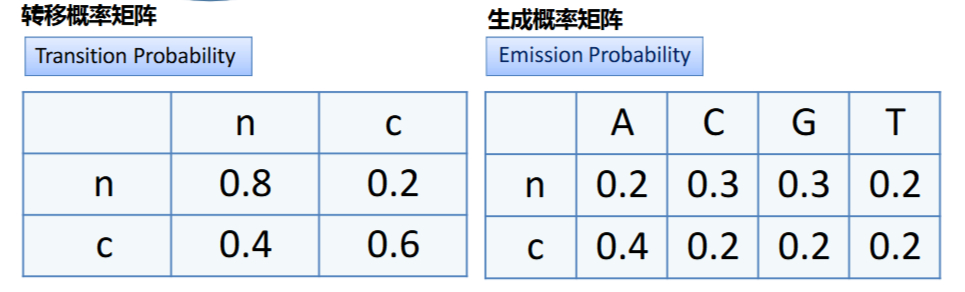
其中n为non-coding area。在有了矩阵之后,根据给定的序列,求其生成概率最大的可能
\[
S = \mathsf{arg max} P(S|X)
\]
利用动态规划的思想,那么
\[
P_{coding}(i+1) = e_{coding}(x+1) \max\{P_k(i)p_{k\rightarrow coding}\}
\]
其中\(k\in\{coding, non-coding\}\),是转移概率;对于non-coding的概率,同理,不赘述
上面的计算会造成大量的乘法计算,对于计算机而言很慢,使用对数变为加法,那么新的矩阵就是
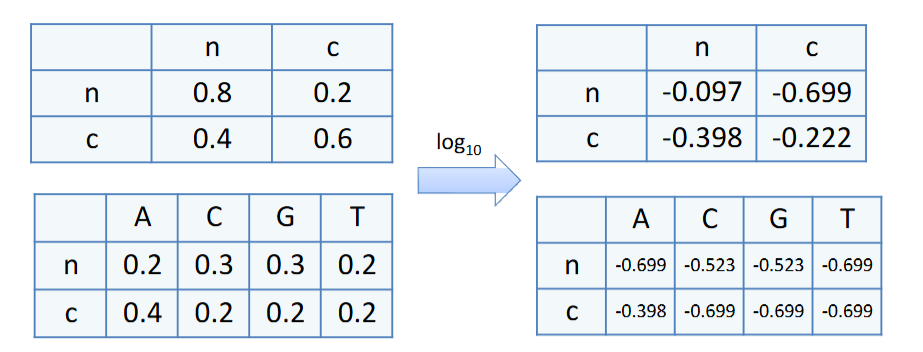
列出表格,进行填充;与全局/局部比对不同,此时没有竖直方向的箭头
假设初始概率\(\pi(P(N)=0.7, P(C)=0.3)\),那么对数化后就是\(-0.155, -0.523\)
对于序列CG,表格为
| C | G | |
|---|---|---|
| non-coding | -0.155+(-0.523)=-0.678 | -0.678+(-0.097-0.523)=-1.298 |
| coding | -0.523+(-0.699)=-1.222 | -0.678+(-0.699-0.699)=-2.076 |
最大概率是CG均为非编码区
例:判断一阶HMM是否在以下场景适用
- 通过股票价格波动推断市场情绪
- 可以,隐藏状态是市场情绪,观测值是价格、交易量等;局限:短期有效
- 通过笔迹轨迹识别书写字符
- 可以,隐藏状态是字符,观测值是笔迹的轨迹;字符独立,符合HMM假设
- 预测十年后平均温度
- 不行,长期依赖不能预测
- 自动驾驶根据传感器数据规划路径
- 不行,HMM离散状态假设不正确
- 根据脑电信号对癫痫发作预测
- 分两类:适用:通过脑电推测电线前期状态;不适用:脑电信号可以划分地更简单,用分类模型就行
- 通过传感器振动信号推断设备健康状态
- 可以,隐藏状态是设备状态,观测值是传感器信号;HMM模型广泛用于状态退化建模
- 通过视频帧序列推断人体动作
- 不行,一阶不行
1.4 多序列比对
1.4.1 用途
- 进化分析:鉴定物种的同源性,建立系统发育树,测试进化模型
- 功能分析:在蛋白质对比中鉴定保守区域,鉴定蛋白质家族
- 结构分析:识别序列的共同变化,用于同源性建模
- 鉴定保守的引物结合位点,用于突变分析的诱变实验等
下面的例子展示了蛋白质的保守性质
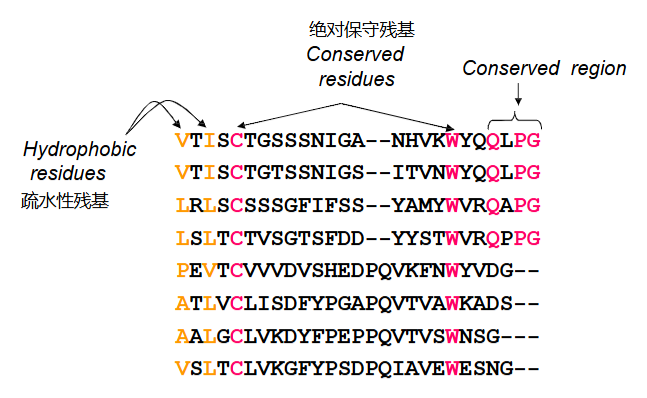
1.4.2 比对方法
比对和 打分法:Sum-of-pairs scoring
将序列两两进行比对,累和所有的分数,一共对比\(C_n^2\)次
渐进式比对
用于已经归类的子组之间的比对,组间序列顺序不可变,Gap只能加不能减
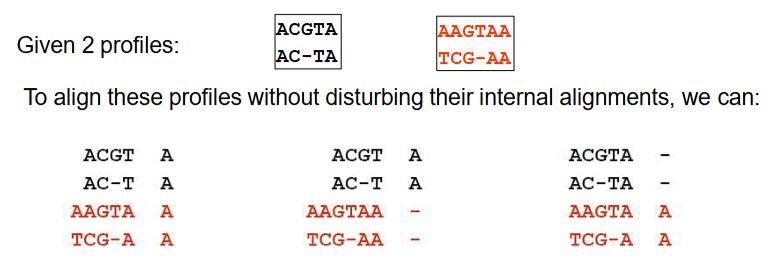
Clustal
采用全局序列比对法进行所有序列的两两比对,构建距离矩阵(即差异性矩阵),矩阵用于聚类算法的分析
1.4.3 DNA vs Protein
哪个对比更有说服力?蛋白质
因为DNA/核酸只有4种碱基,其变化更少,随机匹配更加不准确,即序列的独特性不足,易匹配错误
而氨基酸的残基有20多种,更难配错
当使用DNA很难匹配时,可以将其翻译为蛋白质进行比对