7 图像复原
图像增强是主观的,提高图像的可懂性;图像复原是客观的,提高图像的保真度
7.1 图像退化模型
图像退化的因素
- 噪声干扰:在采集过程中的噪声,或者探测器损坏
- 运动模糊:被采集物体运动产生的模糊,运动伪影
- 几何失真:由于成像过程的系统非线性造成
- 辐射失真:传输介质的不均一,如大气湍流等
- 成像系统的像差、畸变、带宽有限等
- 灰度失真:系统本身的亮度响应不均匀,同亮度的灰度不同
一般是非线性的
建立图像退化模型是复原的第一步,大致如下
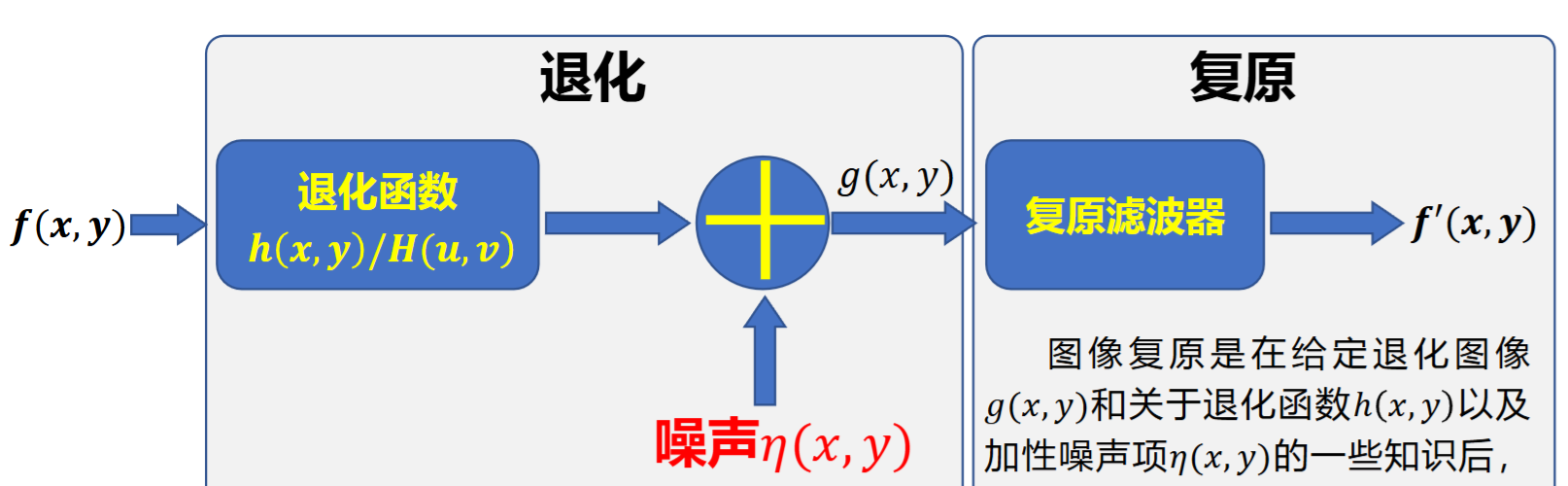
得到退化图像为
\[
g(x,y) = f(x,y)*h(x,y) + \eta(x,y) \\
G(\mu,\nu) = F(\mu,\nu)\cdot H(\mu,\nu) + \Eta(\mu,\nu)
\]
其中\(\Eta\)是大写的\(\eta\)
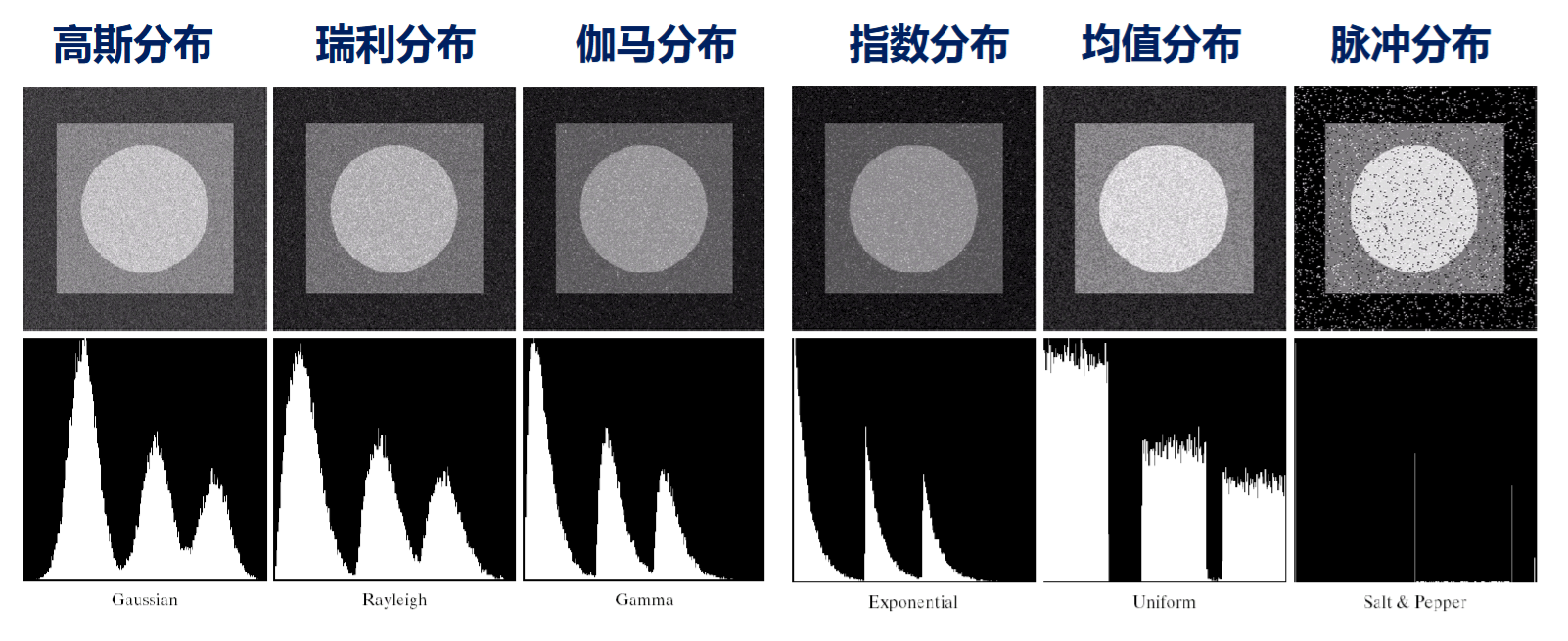
7.2 常见噪声模型
7.2.1 高斯噪声
来源
- 视场不够明亮,亮度不均匀
- 元件自身的热噪声
- 长期工作的高温,产生噪声
分布
\[
p(z) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(z-\mu)^2}{2\sigma^2}}
\]
其中\(z\)是灰度值,均值为0的噪声(\(\mu = 0\))又称白噪声
7.2.2 瑞利噪声
来源:平坦衰落信号的接收包络或是多路径分量的接收包络(雷达)
分布
\[
p(z) = \begin{cases}
\frac{2}{b}(z-a)e^{-\frac{(z-a)^2}{b}} , \,\,\,\, z\geq a\\
0\,\,\,\,\,\,\,\,\,,o.w.
\end{cases}
\]
均值和方差为
\[
\mu = a+\sqrt{\frac{\pi b}{4}}\\
\sigma^2 = \frac{b(4-\pi)}{4}
\]
7.2.3 γ噪声
来源:激光成像的噪声,pet等
分布
\[
p(z) = \begin{cases}
\frac{a^bz^{b-1}}{(b-1)!}e^{-az},\,\,\,\,z\geq 0\\
0 ,\,\,\,\,\,\,\,\,\, o.w.
\end{cases}
\]
均值和方差为
\[
\mu = \frac{b}{a}\\
\sigma^2 = \frac{b}{a^2}
\]
其中\(a>0, b\in \Z^+\),当\(b=1\)时,退化为指数分布
7.2.4 均匀分布噪声
来源:一定范围内的模拟输入被量化为一个数字输入,如果模拟信号的幅值时随机的,那么量化误差是均匀分布的
分布
\[
p(z) = \begin{cases}
\frac{1}{b-a} ,\,\,\, a\leq z \leq b\\
0,\,\,\,\,\, o.w.
\end{cases}
\]
均值和方差为
\[
\mu = \frac{a+b}{2}\\
\sigma^2 = \frac{(b-a)^2}{12}
\]
7.2.5 脉冲噪声(椒盐噪声)
来源:受到强烈的脉冲信号干扰
分布
\[
p(z) = \sum P_i\delta(z-i)
\]
其中高灰度的噪声为盐噪声(白点),低灰度的噪声为胡椒噪声(黑点)
7.2.6 周期噪声
来源:由于电气或电机干扰产生,是一种空间依赖型噪声,可以通过频域滤波显著减少

7.3 噪声处理
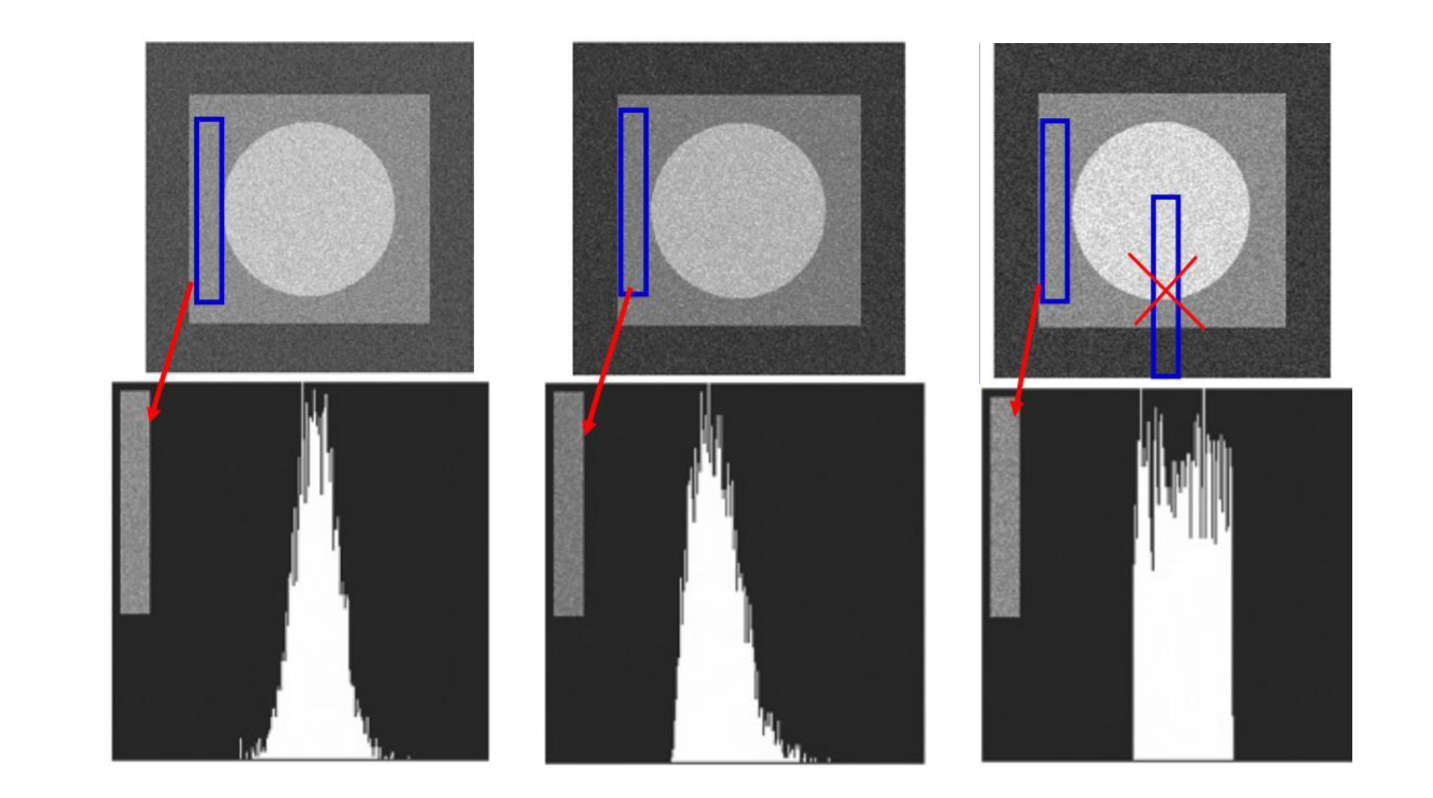
7.3.1 噪声参数估计
当只有加性噪声存在时,图像增强和图像复原几乎一致
根据直方图进行估计,但是要注意不能找边界处进行直方图处理
7.3.2 均值滤波器
算数均值就是上面的平滑,不赘述
几何均值滤波器
利用邻域内的几何均值进行计算
\[
\hat{f}(x,y) = \left( \Pi g(s,t)\right)^\frac{1}{mn}
\]
但是需要注意,当邻域内存在0时,这个滤波器不好用
即对椒噪声不好用
谐波均值滤波器
利用调和平均数进行计算
\[
\hat{f}(x,y) = \frac{mn}{\sum \frac{1}{g(x,y)}}
\]
这对高灰度的盐噪声很好,但是同样对胡椒噪声不好用;善于处理高斯噪声
逆谐波均值滤波器
\[
\hat{f}(x,y) = \frac{\sum g(s,t)^{Q+1}}{\sum g(s,t)^Q}
\]
其中\(Q\)是滤波器的阶数
当\(Q>0\)时,善于处理胡椒噪声;当\(Q<0\)时,处理盐噪声;不能同时处理两种噪声
当\(Q=0\)时,退化为算术均值滤波器;当\(Q=-1\)时,退化为谐波均值滤波器
7.3.3 统计排序滤波器
中值滤波
\[
\hat{f}(x,y) = \mathsf{mid}\{g(s,t)\}
\]
对单极或双极脉冲噪声很有效
最值滤波器
分为最大/小值,在发现图像的亮/暗点有效,对胡椒/盐噪声有效
中点滤波器
\[
\hat{f}(x,y) = \frac{1}{2}\left(\max \{g(s,t)\} + \min \{g(s,t)\}\right)
\]
结合了排序和平均,对高斯和均匀噪声效果好
修正的α均值滤波器
\[
\hat{f}(x,y) = \frac{1}{mn-d} \sum g_d(s,t)
\]
其中\(f_d\)表示在邻域内分别去除\(d/2\)个最高和最低值后的集合
结合了中值和均值,对多种混合噪声的效果好,如高斯+椒盐
7.3.4 自适应局部降噪滤波器
可以根据局部的统计特征自动调整滤波效果
\[
\hat{f}(x,y) = g(x,y) - \frac{\sigma^2_\eta}{\sigma^2_L}[g(x,y)-m_L]
\]
其中\(\sigma_\eta^2,\sigma_L^2\)分别是整个图中的噪声方差和邻域内的灰度方差,\(m_L\)表示局部均值
分为以下几种情况
- \(\sigma^2_\eta=0\),即没有噪声,那么\(\hat{f}=g\)
- \(\sigma_L>>\sigma_\eta\),那么这里是边界突变点,不能平滑,\(\hat{f}=g\)
- \(\sigma_L\approx \sigma_\eta\),那么这里是噪声,可以用普通的均值滤波,\(\hat{f}=m_L\)
- \(\sigma_L<\sigma_\eta\),根据加性噪声假设,令二者相等,\(\hat{f} = m_L\)
7.3.5 自适应中值滤波器
中值滤波器的效果受窗口大小影响
小的窗口能保护细节,但是对噪声过滤不好,大的反之;且当噪声的数目多于正常像素数目,结果会是噪声
根据局部统计值动态调整窗口大小
整个流程如下
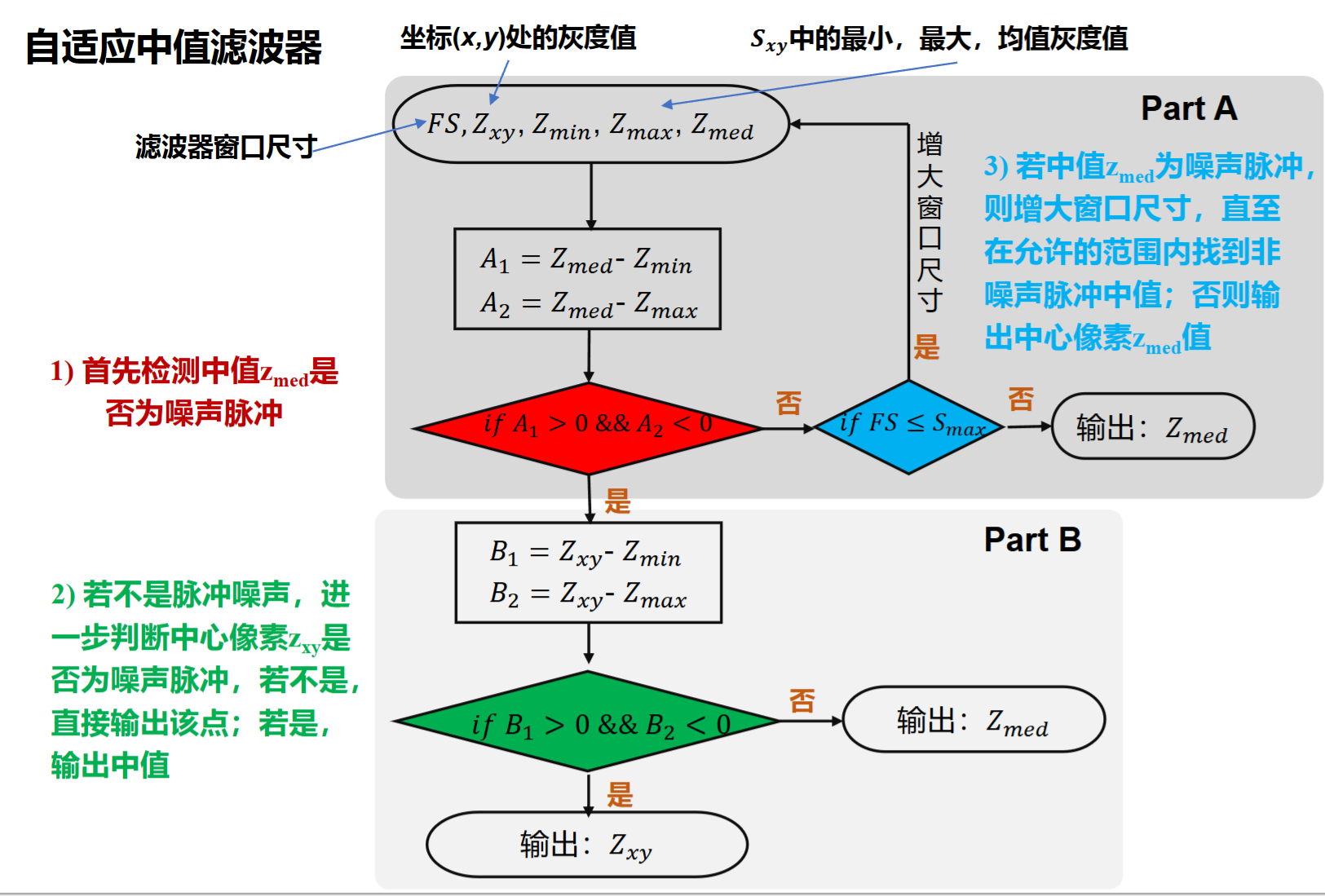
基本想法就是噪声不能是中值,所以判断条件没有\("="\),还需要一个窗口的最大值作为限制
去噪的效果类似于中值,但是保留了很多细节
7.3.6 频率域消除周期噪声
由于周期噪声在频域内就是几个离散的点,可以使用带阻滤波器进行过滤
几个常用的带阻滤波器
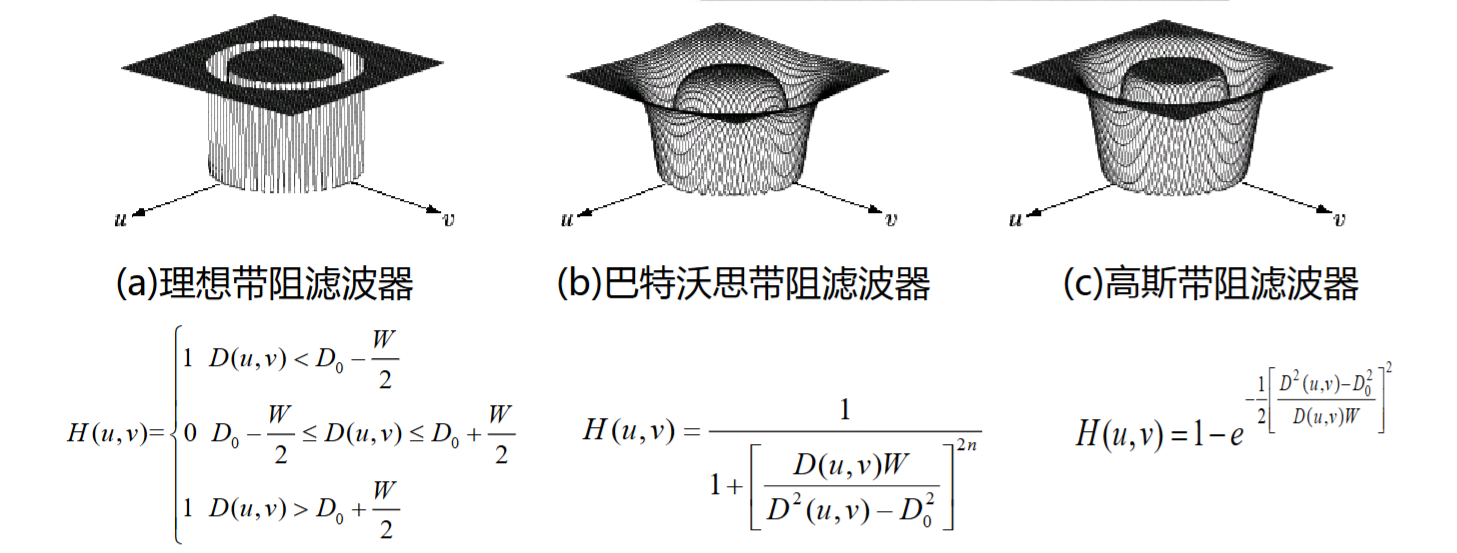
如果使用\(H_p = 1-H_R\)得到带通滤波器
对同一幅图像进行处理,带通会得到周期性噪声,带阻得到去噪图像,因为是互补的
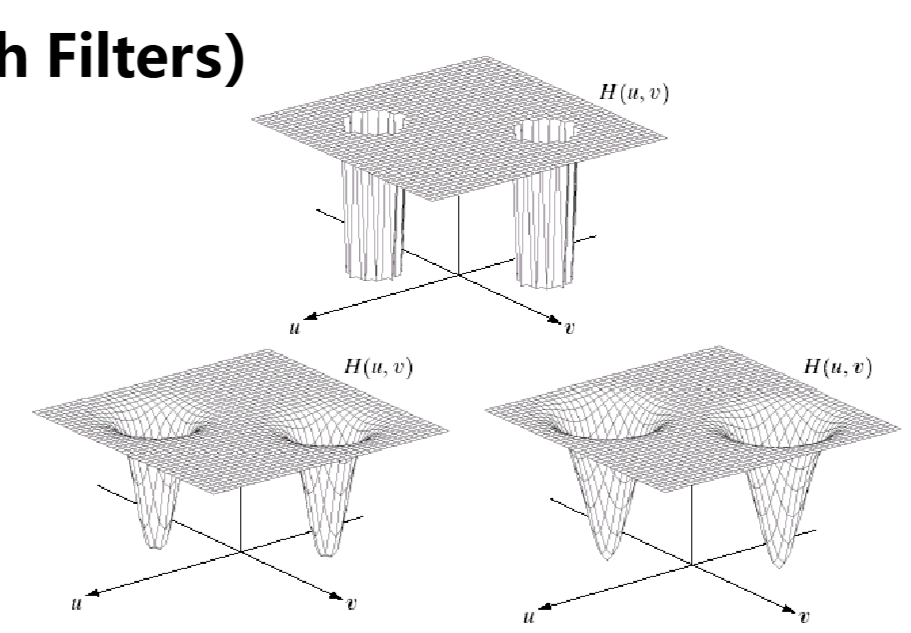
有时候周期噪声没有明显的频带,使用陷波滤波器
陷波滤波器阻止/通过实现定义的中心频率的邻域内的信号
由于傅里叶变换的对称性,噪声信号应该是中心对称的,因此滤波器也需要中心对称
但是陷波区的形状和数目是任意的
7.4 估计退化函数
找到退化函数\(H(\mu,\nu)\)是图像复原的关键,有以下方法
7.4.1 图像观测估计法
在图像没有明显噪声的地方进行取样,得到子图像\(g_s(x,y)\),利用无噪声重建得到\(f_s(x,y)\),那么退化函数为
\[
H(\mu,\nu) = \frac{G_s(\mu,\nu)}{F_s(\mu,\nu)}
\]
7.4.2 实验估计法
利用冲激函数,得到系统的冲激响应,做实验
\[
\delta(x,y) \rightarrow h(x,y) \Rightarrow1\rightarrow H(\mu,\nu)
\]
7.4.3 模型估计法
从引起图像退化的基本原理进行推导,根据先验的模型
例如,已知大气湍流函数为
\[
H(\mu,\nu) = e^{-k(\mu^2+\nu^2)^{5/6}}
\]
那么
\[
G = HF \Rightarrow F = H^{-1}G
\]
运动伪影
设\(x_0(t),y_0(t)\)是\(t\)时刻的位置分量,曝光时间为\(T\)的图像得到结果是
\[
g(x,y) = \int_0^T f(x-x_0(t),y-y_0(t)) dt
\]
两边DFT,由于积分不含位置项,等价于对\(f\)进行DFT,得到
\[
G = \int _0^T F \cdot e^{-j2\pi(\frac{\mu x_0(t)}{M}+\frac{\nu y_0(t)}{N})}dt
\]
那么系统函数就是
\[
H =\int _0^Te^{-j2\pi(\frac{\mu x_0(t)}{M}+\frac{\nu y_0(t)}{N})}dt
\]
7.5 图像复原方法
分为逆滤波和维纳滤波
7.5.1 逆滤波
\[
\hat{F} = \frac{G}{H} = F + \frac{\Eta}{H}
\]
当\(|H|\rightarrow 0\)时,噪音会变得很大,因此加入一个小的常数\(k\),改写为
\[
\hat{F} = \frac{G}{H+k}
\]
逆滤波的问题在于完全没有考虑到噪声的统计特性
7.5.2 维纳滤波
令
\[
\hat{F}(\mu,\nu) = H_{wie}(\mu,\nu) \cdot G(\mu,\nu)
\]
通过误差的最小二乘法得出\(H\),即使得
\[
e^2 =\mathsf{E}\left(|F-\hat{F}|^2\right)
\]
最小的\(H\),带入,得到
\[
H_{wie} = \frac{1}{H}\cdot \frac{|H|^2}{|H|^2+\frac{S_\eta}{S_f}}
\]
注意,这个结果的前提是噪声的均值为0且与图像独立
其中\(S_\eta,S_f\)分别是噪声和原图的功率谱,有\(S_\eta(\mu,\nu)=\mathsf{E}\{ |\Eta(\mu,\nu)|^2 \}\),\(S_f\)同理
当二者未知时,用\(K\)代替
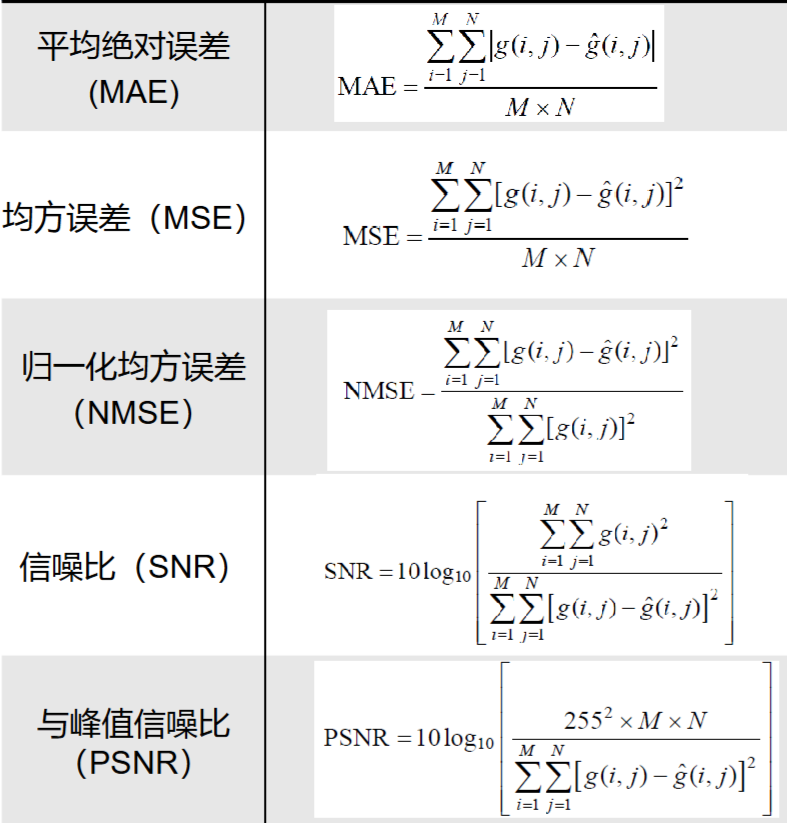
7.6 图像复原的质量评价
有主观和客观,主观就是人看,客观就是与原图的误差的统计值,常用的统计值如下