6 频域滤波图像增强

学习笔记
作者: MingXiao

6.1 傅里叶变换

6.1.1 基本概念

使用二维傅里叶变换将图像从空间域变换到频率域，公式如下
\[ F(\mu, \nu) = \int_\infty\int_\infty f(x,y) e^{-j2\pi(\mu x+\nu y)}dxdy\\ f(x,y) = \int_\infty\int_\infty F(\mu, \nu)e^{j2\pi(\mu x+\nu y)}d\mu d\nu \]
这是连续图像，一般用的是数字图像，那么退化为DFT，公式如下
\[ F(\mu, \nu) = \sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2\pi\left(\frac{\mu x}{M}+\frac{\nu y}{N}\right)}\\ f(x,y) = \frac{1}{MN} \sum_{\mu=0}^{M-1}\sum_{\nu =0}^{N-1} F(\mu, \nu)e^{j2\pi\left( \frac{\mu x}{M}+\frac{\nu y}{N}\right)} \]
其中\(\mu=0,1,\ldots,M-1, \nu=0,1,\dots, N-1\)

注意，图像中心往往是一个幅值非常大的点，需要对DFT后的图像做对数变换

正常情况下，做完DFT后中心是高频信号，四周是低频信号，需要进行fftshift，将低频信号放在中心，因为人脑习惯这么思考

需要做如下变换，实际上，后文中所有的\(F(\mu,\nu)\)都是下面的形式
\[ F(\mu, \nu) \rightarrow F\left(\mu - \frac{M}{2}, \nu - \frac{N}{2}\right) \]
那么对应到空间域中，
\[ f(x,y) \rightarrow f(x,y)(-1)^{x+y} \]

对于实信号，\(F(\mu,\nu)\)是共轭对称的，所以采集一半就行；但是一般会多采一点，用于相位矫正

6.1.2 几个性质

  1. 线性

  2. 空间域位移 等价于 频率域相移；频率域位移 等价于 空间与相移

  3. 旋转
    \[ f(r, \theta+\theta_0) \leftrightarrow F(\omega,\phi+\theta_0) \]
    其中，\(\omega = \sqrt{\mu^2+\nu^2}, \phi = \tan^{-1}\frac{\nu}{\mu}\)

    简言之，即空间域和频率域图像旋转相同角度

  4. 可分性

    即\(x,y\)独立，可以先后变换

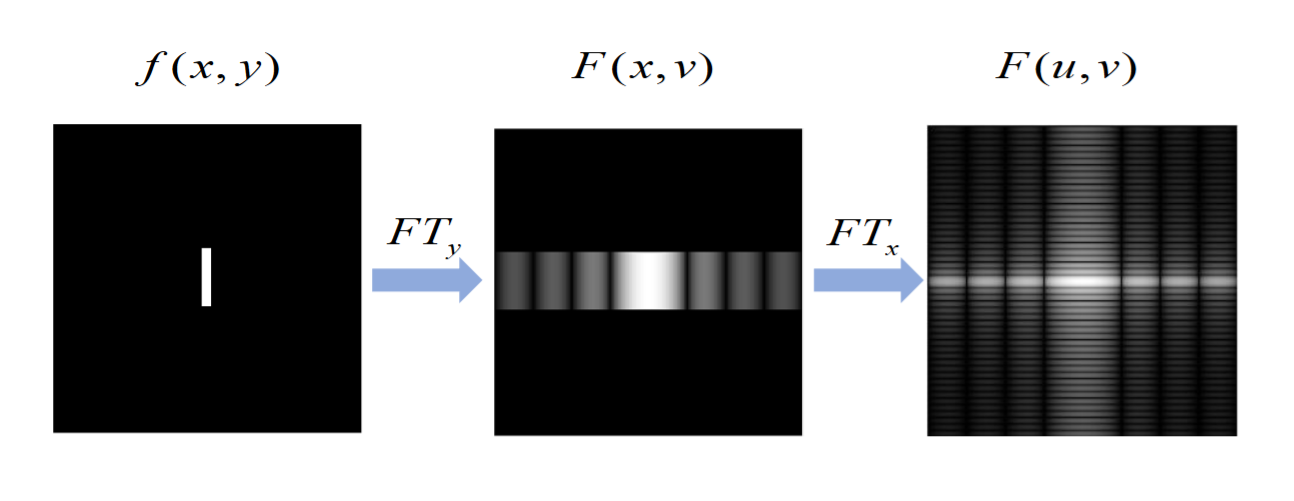
  5. 均值定理
    \[ \overline{f}(x,y) = \frac{1}{MN}F(0,0) \]

  6. 对称性，即实函数的傅里叶变换共轭对称

  7. 周期性，即DFT周期延拓为DFS

  8. 卷积定理
    \[ f(x,y) * h(x,y) \leftrightarrow F(\mu, \nu)\cdot H(\mu, \nu)\\ f(x,y)\cdot h(x,y) \leftrightarrow F(\mu, \nu) *H(\mu,\nu) \]

6.1.3 频率域图像增强

图像的频谱反应了什么？

频谱的直流低频分量，代表图像的平滑区域；交流高频分量，代表图像的边界区域

因此，可以根据这个特点在频域上对图像进行滤波

主要步骤

  1. fftshift， \(f(x,y)(-1)^{x+y}\)，这步非常重要
  2. DFT，得到\(F(\mu-M/2, \nu-N/2)\)
  3. 使用滤波器\(H(\mu, \nu)\)与\(F(\mu, \nu)\)相乘
  4. 反变换得到\(g(x,y)(-1)^{x+y}\)，注意需要反转一下，得到滤波图像

6.2 低通滤波

消除随机噪声，减弱边缘效应，平滑图像

常用的滤波器：理想低通；巴特沃斯低通；高斯低通

6.2.1 理想低通

物理上做不到，只能在计算机中实现
\[ H(\mu, \nu)= \begin{cases} 1\,\,\,\, , D(\mu, \nu)其中\(D(\mu,\nu)\)是点\((\mu,\nu)\)到图像中心的欧氏距离

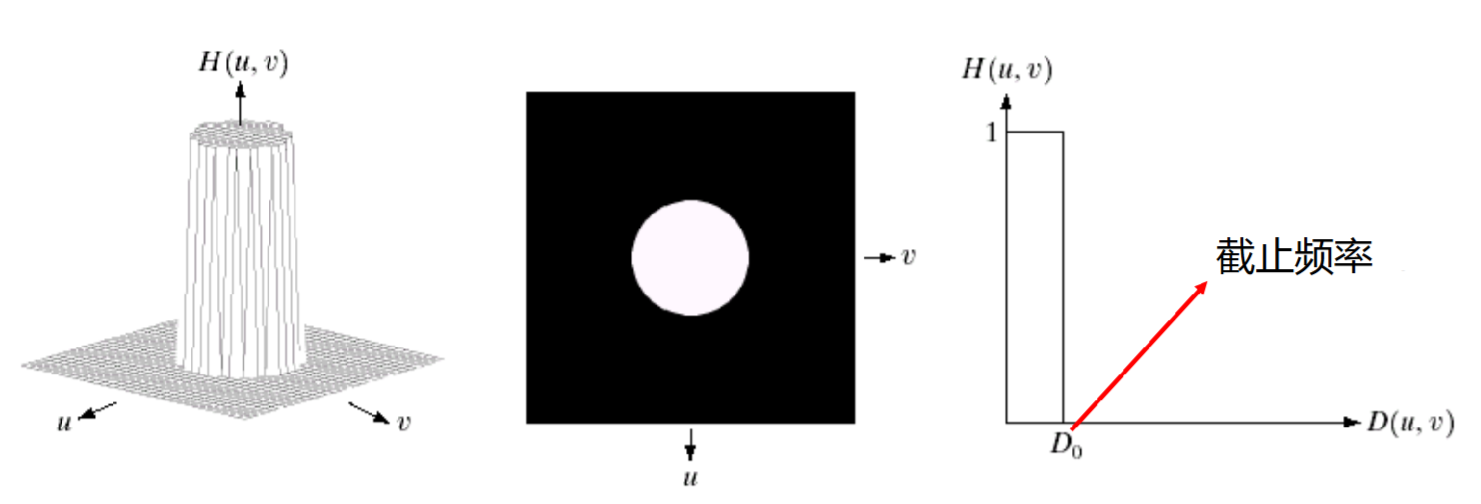
但是，使用理想低通滤波器产生的图像，存在振铃现象（吉布斯效应，图像还是连续的，一定会存在sinc函数）

这个现象在图像的边界等突变点最明显

6.2.2 n阶巴特沃斯低通

\[ H(\mu, \nu) = \frac{1}{1+[D(\mu,\nu)/D_0]^{2n}} \]

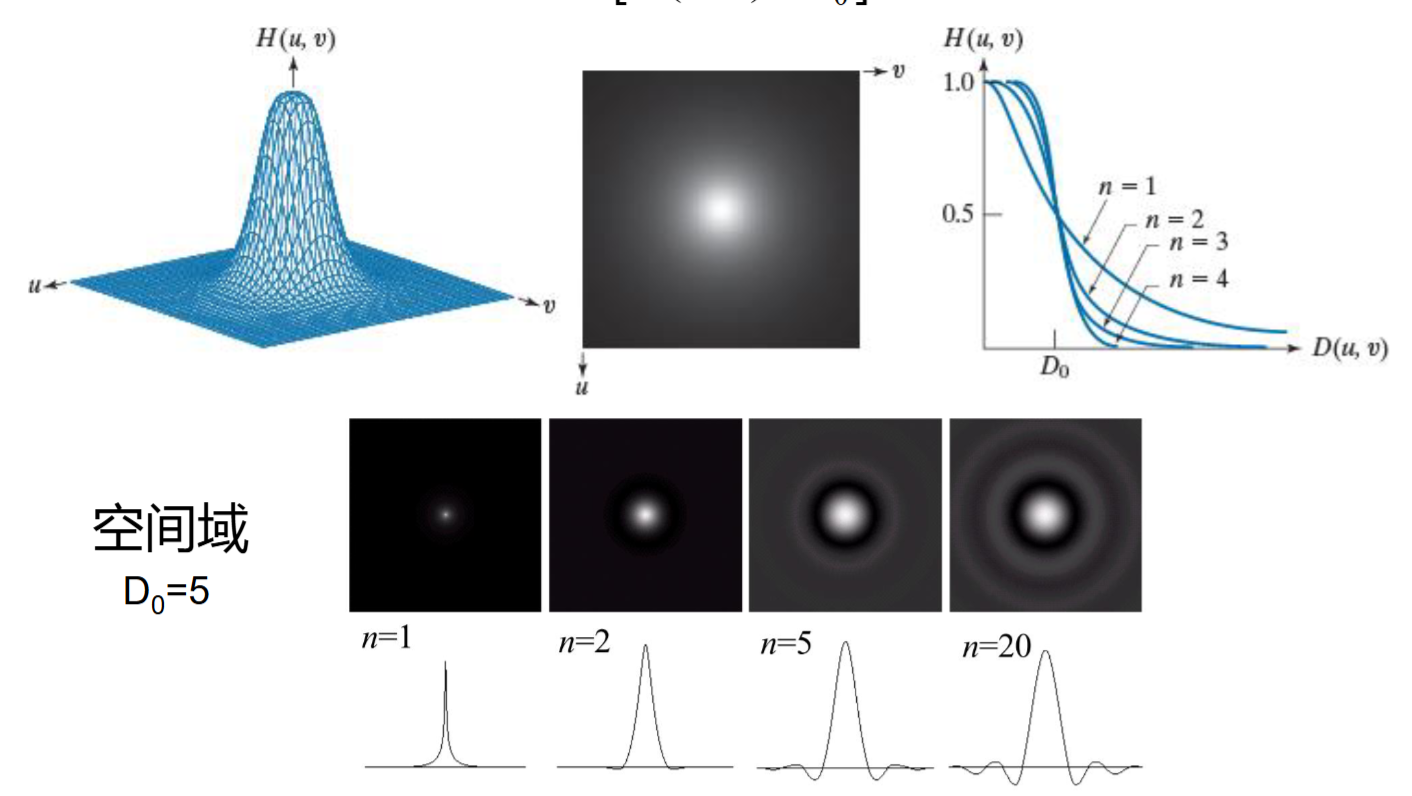
截止频率处变化地更平滑

相比于理想低通，它

  1. 没有明显突变，导致了吉布斯现象很弱
  2. 过渡平滑，模糊程度减少
  3. 但是相对的，尾部的高频成分也更多，平滑效果没理想低通好

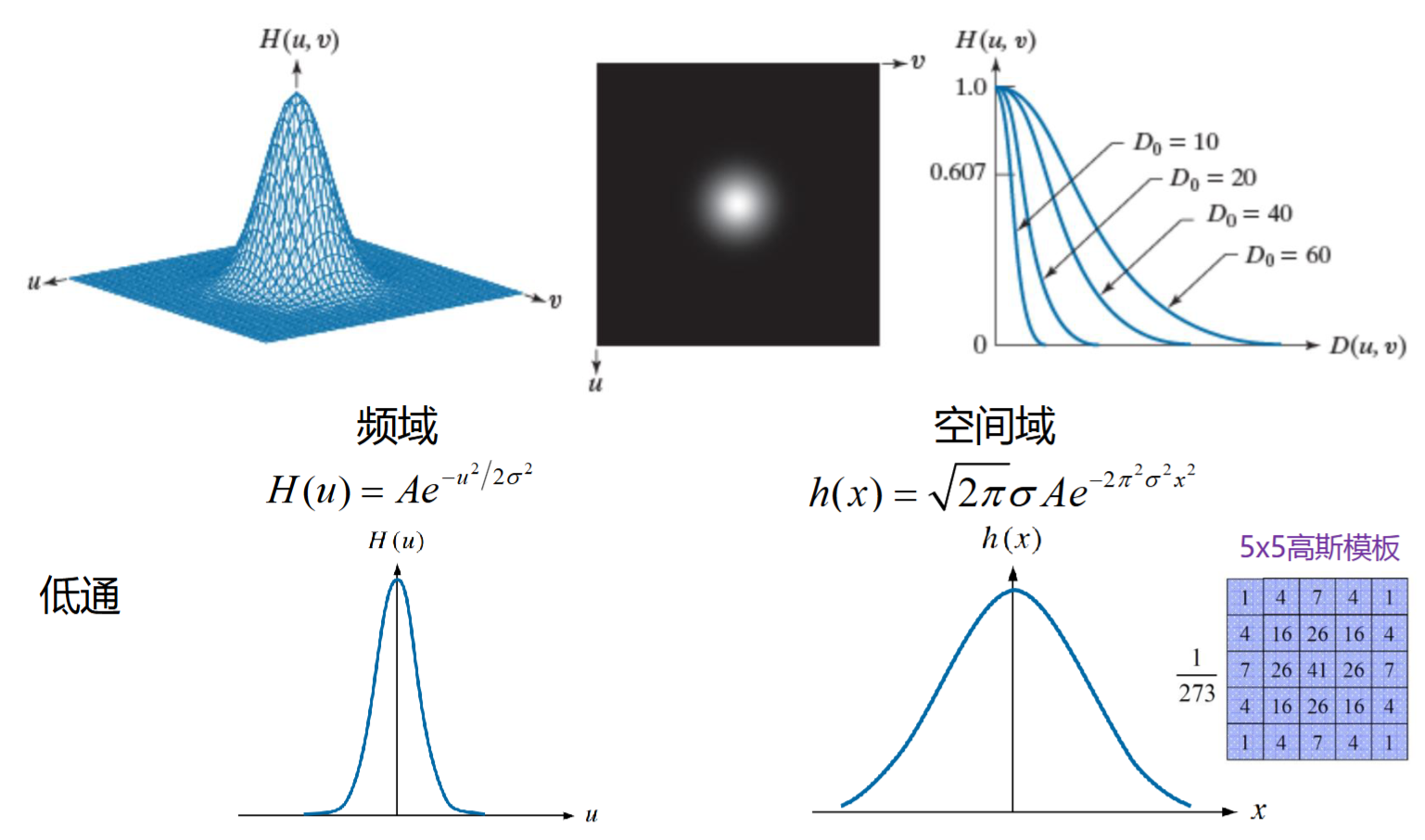
6.2.3 高斯低通

\[ H(\mu, \nu) = e^{-D^2(\mu,\nu)/2D_0^2} \]

几个典型应用：将破碎的文字片段连接起来；减少眼角皱纹；减小水平扫面线对宏观边界检测的影响

6.3 高通滤波

增强图像的边缘，起到锐化作用

常见的高通滤波器有：理想高通；巴特沃斯高通；高斯高通；频域拉普拉斯；高频加强锐化等

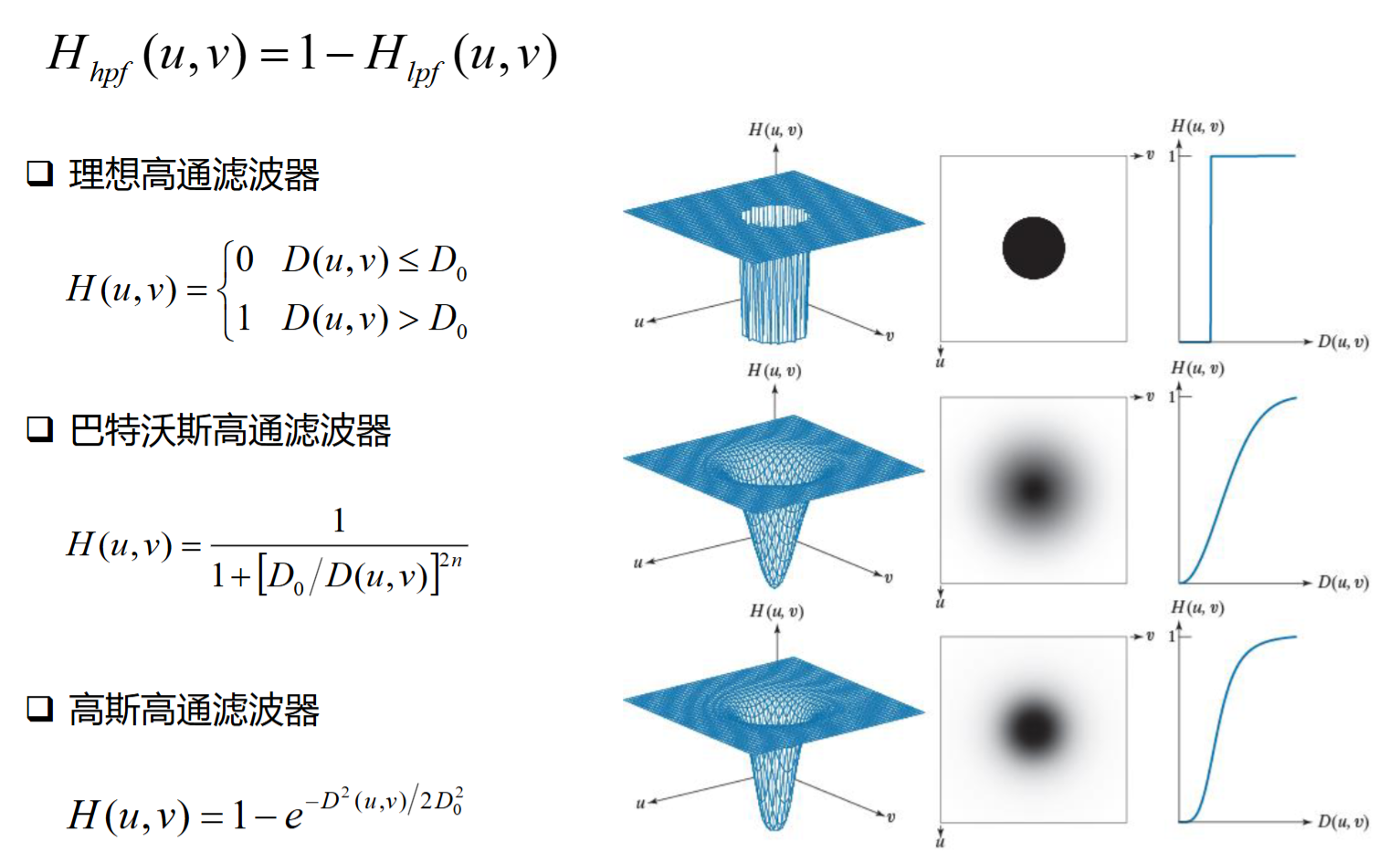
6.3.1 与低通对应

既然低通已经存在了，那么将\(H_h = C - H_l\)不就行了吗？

6.3.2 频域拉普拉斯

空间域的拉普拉斯算子由上可知，根据傅里叶变换的性质，得到
\[ \mathcal{F}\{\nabla ^2f(x,y)\} = -(\mu^2+\nu^2)F(\mu,\nu) \]
利用了\(\frac{df}{dx} \leftrightarrow j\mu F\)

那么传递函数为
\[ H(\mu, \nu) = -(\mu^2+\nu^2) \]
为了shift，平移滤波器，得到
\[ H(\mu,\nu) = -[(\mu-M/2)^2+(\nu-N/2)^2] \]
为什么\(H\)也要平移？：对原图先Laplace，然后再\((-1)^{x+y}\)，即\((\nabla^2f(x,y))(-1)^{x+y}\)

即
\[ \nabla^2 f(x,y) \leftrightarrow H(\mu,\nu) F(\mu,\nu) \]

6.3.3 高频加强图像增强

\[ g(x,y) = \mathcal{F}^{-1}\{[k_1+k_2H_{h}(\mu,\nu)]F(\mu,\nu)\} \]

就是将高频信息叠加到原图上

6.4 同态滤波

非均匀光照的处理：同态滤波，顶帽变换，凸壳处理，滑动平均阈值处理手写/打印图像

研究问题：非均匀光照或非均匀强度检测的图像，二者都能近似表达为
\[ f(x,y) = i(x,y)r(x,y) \]
其中前者是检测器分量，后者是检测量分量，在非均匀光照的例子中，前者是不均匀的光照，后者是光反射分量（即成像灰度）

目标是实现亮度调整和对比度提升，消除非均匀光照的影响

考虑到人眼对图像亮度的响应类似于对数运算，可以对\(f\)取对数进行计算

由此引入同态滤波，这是一种将频率过滤和灰度变化结合的方法，优点是符合人眼的响应，避免了直接变换的失真

流程如下：

经过取对数之后，\(\ln f = \ln i + \ln r\)，其中\(\ln i\)是变化缓慢的低频分量，利用傅里叶的线性性可以解

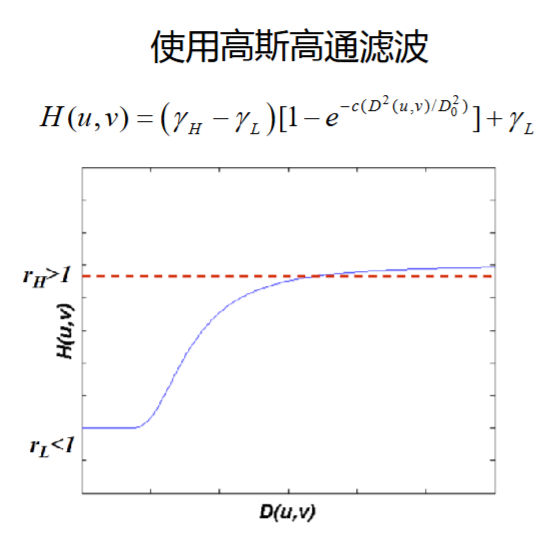
为了压制\(\ln i\)，同时增强高频的反射分量\(\ln r\)，可以构造一个滤波器
\[ H(\mu,\nu) = (\gamma_h-\gamma_l)H_h(\mu,\nu) +\gamma_l \]
其中\(\gamma_h >1,\gamma_l < 1\)，\(H_h\)为高通滤波器



Comments