5 图像分割
图像处理的整个过程
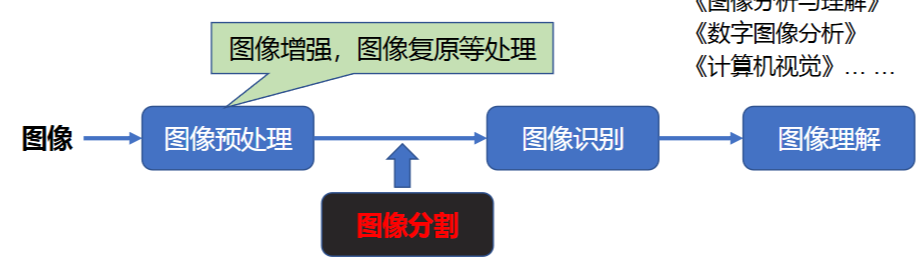
5.1 图像分割基础
\(R\)表示全图,\(R_i\)表示分割后的图像的子图,有以下条件
- \(R = \bigcup R_i\),分割必须完全
- \(R_i\)是一个联通集
- \(R_i \cap R_j=\phi (i\neq j)\),各个区域不相交
- \(P(R_i)=True\),\(R_i\)必须满足一定的属性(谓词逻辑)
- \(P(R_i\cup R_j)=False\),其中\(R_i\)和\(R_j\)邻接,任意两个相邻区域不能同时满足一个属性
5.2 区域间不连续
有三类不连续的灰度:点(孤立点);线(较细);边缘(相连边缘像素集合)
由于一阶微分处理通常会产生较宽的边缘,二阶微分处理对细节有较强的响应(细线/孤立点),在不同情况下用不同的算法
5.2.1 孤立点检测
使用空间拉普拉斯算子\(\nabla^2f=\frac{\part^2f}{\part x^2}+\frac{\part^2f}{\part y^2}\)
\[
\left|
\begin{matrix}
-1&-1&-1\\
-1& 8&-1\\
-1&-1&-1\\
\end{matrix}
\right|
\]
整个过程的流程如下
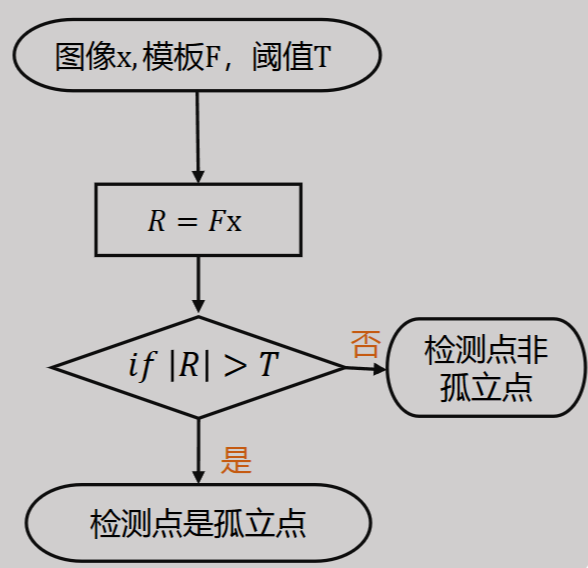
当\(R\)的值足够大才能说明这个点是孤立的点
5.2.2 线检测
也使用上面的算子,但是这样会产生正负的值,有以下的处理情况
- 取绝对值:得到的线宽会加宽
- 取正值:获得单线
- 存在噪声:取阈值
由于存在山谷效应(较宽的线中间没有响应),线检测通常指细线,宽度小于卷积核大小
而且拉普拉斯核是各向同性的,响应与线的方向无关,设计和方向有关的检测核

左上角是原图,右上角是阈值变换,左下角是取了绝对值,右下角是取了正值
可以发现有些较粗的线只有边缘,中间没了
规定线方向检测核
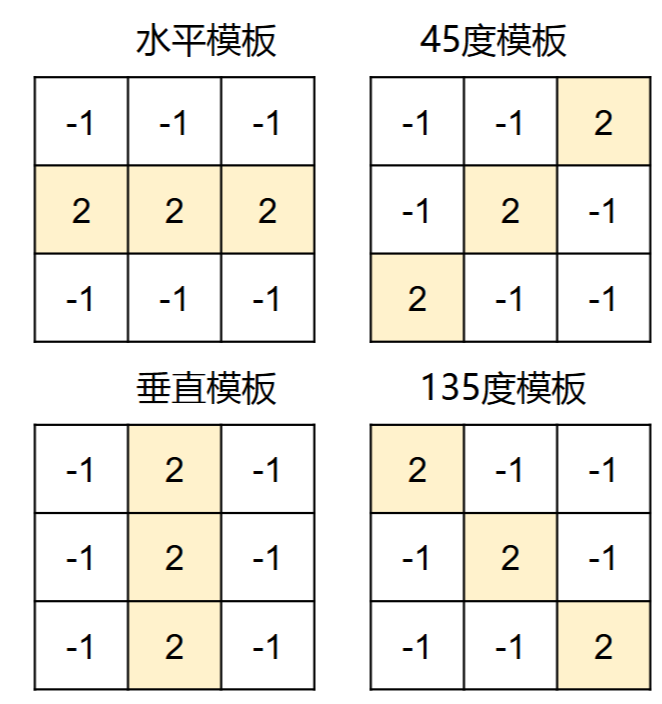
注意卷积操作会中心对称模板,模板设计要注意以下标准
- 可以大于3*3
- 模板系数和为0
- 感兴趣的方向系数大
5.2.3 边缘检测
存在3种边缘模型
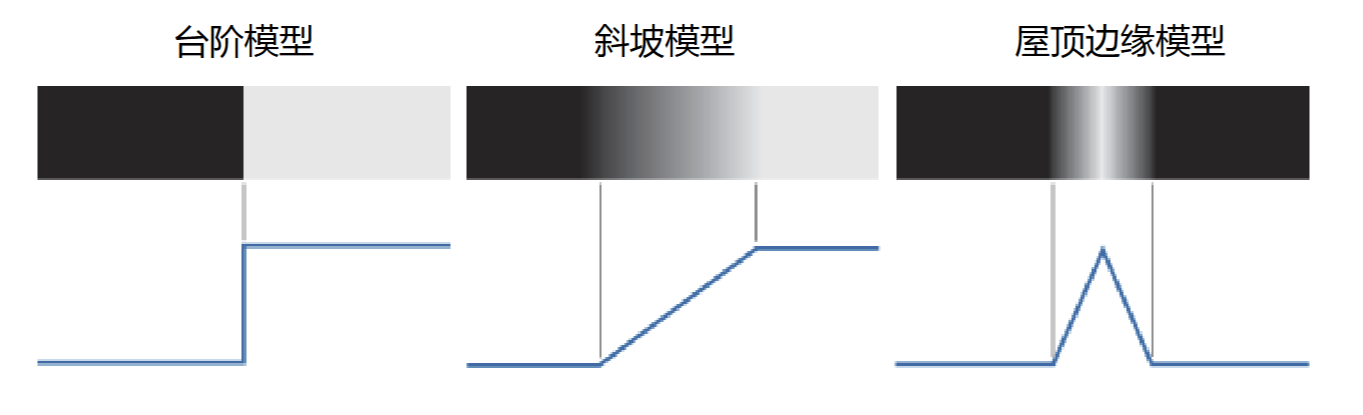
边缘检测的原理:导数在边缘方向取到极值
基本思路:计算局部的一、二阶导数
- 一阶导数直接定位边缘点
- 二阶导数的过零点可以定位边缘的中心
- 二阶导数对噪声敏感,有时不好用,可以先平滑
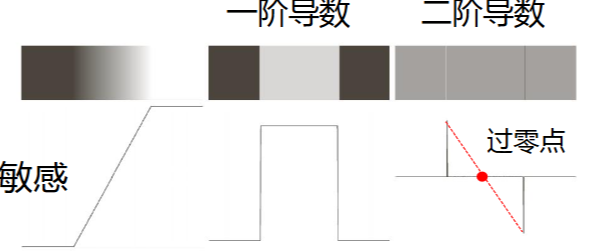
不同操作的结果如图
常见边缘检测方法
梯度算子
- 基本梯度算子
- Roberts算子
- Prewitt算子
- Sobel算子
以上都是一阶微分算子
拉普拉斯算子,对噪声非常敏感,通常不单独使用
LoG(拉普拉斯高斯算子)
Canny算子
梯度算子
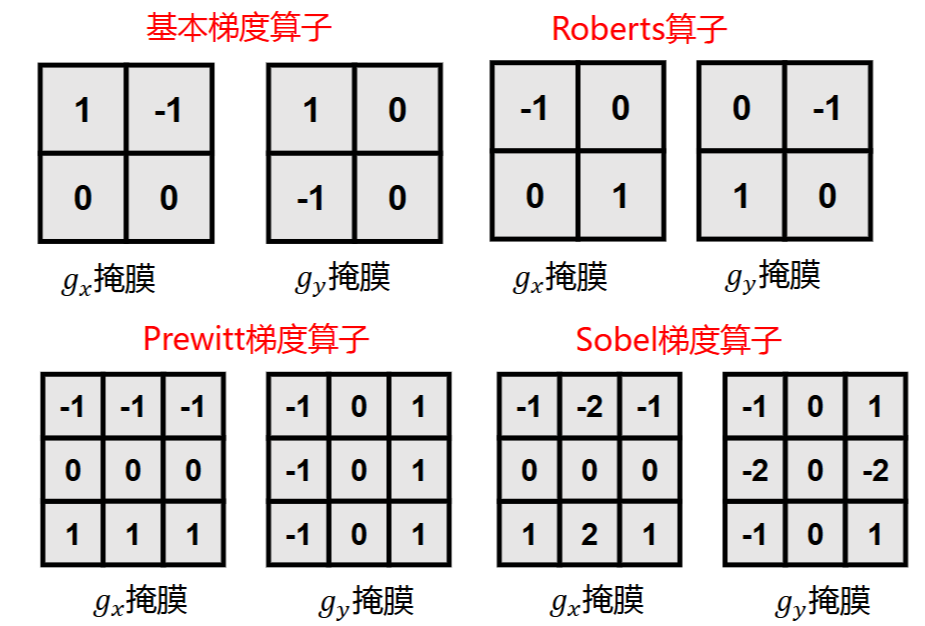
Sobel的y掩膜的右边的-2改为2
梯度幅度为
\[
M(x,y)=|\nabla f(x,y)|=\sqrt{f_x^2+f_y^2} \approx |f_x|+|f_y|
\]
梯度方向为
\[
\alpha(x,y) = \tan^{-1}\frac{f_y}{f_x}
\]
边缘的方向与梯度方向垂直,则
\[
\phi = \alpha(x,y) -90^\circ
\]
上式中\(f_x,f_y,M(x,y), \alpha(x,y)\)都是和原图大小相同的矩阵(边缘补全了)
LoG算子
将高斯滤波和拉普拉斯边缘检测结合在一起,算子为
\[
LoG = \nabla^2G(x,y) = \frac{\part^2G(x,y)}{\part x^2}+\frac{\part^2G(x,y)}{\part y^2}=\frac{x^2+y^2-2\sigma^2}{\sigma^4}e^{-\frac{x^2+y^2}{2\sigma^2}}
\]
等效于先用一个高斯滤波后在用拉普拉斯算子
这个模板对平坦区域无响应,故算子内的系数和应该为0,否则需要调整模板
模板非零部分的大小为\(3\sigma\)为宜,5阶的模板如下
\[
\left|
\begin{matrix}
0&0&-1&0&0\\
0& -1&-2&-1&0\\
-1&-2&16&-2&-1\\
0& -1&-2&-1&0\\
0&0&-1&0&0\\
\end{matrix}
\right|
\]
由于用到了二阶导数,需要使用检测0交叉来定位边缘,过程如下
- 使用一个3*3的领域,检查中心点中心对称元素的符号情况(相乘)
- 符号小于0说明中心点是边缘的中心
- 当存在噪声时,还需要对正负值的绝对值之差进行阈值检测,只有绝对值差的足够小才不是噪声
优点:有平滑滤波,可以克服噪声的影响
缺点:可能产生假边缘(二阶微分缺点);对曲线边缘的定位误差大(对角线都是直的)
Canny算子
Canny提出边缘检测的三大目标
- 低错误率(信噪比高):所有边缘都被检测,没有虚假响应
- 边缘点被很好的定位(定位准确)
- 单个边缘响应:真实边缘周围的局部最大数应该最小
Canny算法流程如下:
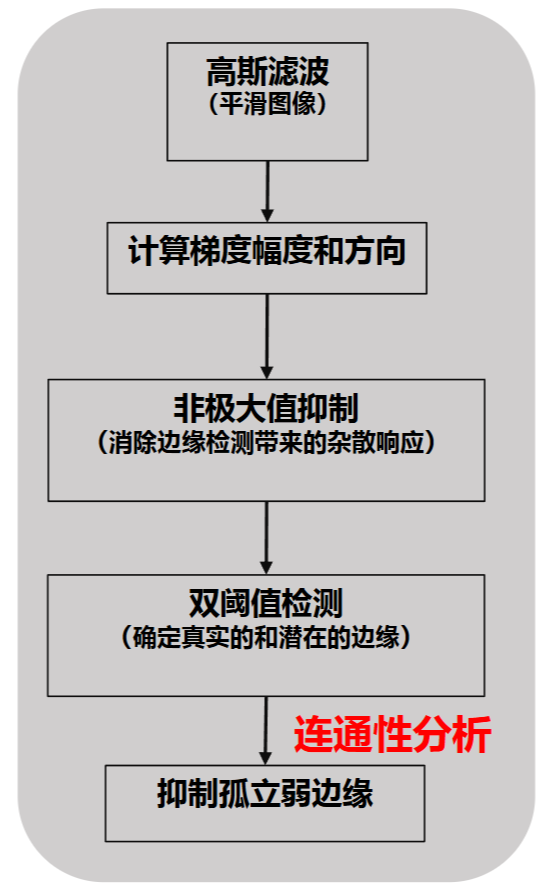
前两个就正常做,使用高斯算子和梯度算子(一阶微分)
第三步,寻找最接近\(\alpha(x,y)\)的方向\(d_k\),若在这个方向上,\(M(x,y)\)小于邻域内的邻点的幅度,则将\(M(x,y)\)置零(非极大值抑制)
第四步,使用两个阈值(一大一小),得到两幅阈值变换的图,记为\(g_H,g_L\),做\(g_N = g_L-g_H\),\(g_N\)只剩下弱边缘;在\(g_H\)中定位强边缘点\(p\),在\(g_N\)对应的点\(p\)处用8联通连接到所有标记为弱边缘的点,这些是真的弱边缘,对所有的\(p\)做此工作;将\(g_N\)中未联通的点置零,这些是噪声;\(g = g_N +g_H\),得到边缘的图像
5.2.4 边缘连接
获取到的边缘可能不连续,需要连接边缘
局部连接处理
在\(S\)邻域内,若有
\[
|M(x,y) - M(s,t)|\leq T
\]
\[ |\alpha(x,y)-\alpha(s,t)|\leq A \]
则认为这是应该连续的边缘,需要将\((s,t)\)连接到\((x,y)\)
在实际处理中上面的方法太复杂,开销大,简化为下面的流程
- 设定阈值大小\(A,T_M,T_A\)
- 令\(g(x,y)=\begin{cases}1,\,\,\,\,\, M(x,y)>T_M\and \alpha(x,y)\in(A\pm T_A)\\0, \,\,\,\,\, o.w.\end{cases}\)
- 得到一个二值图像
- 扫描\(g\)的每一行,在不超过设定的\(L\)的每行中填充(\(g(x,y) = 1\))所有的间隙
- 将\(g\)旋转\(\theta\),扫描\(g(\theta)\)的每一行,重复步骤四,将结构旋转\(-\theta\)
霍夫变换
当找出边界点集之后,有时需要连成线才能看出特征,需要连线
直接一根根连时间复杂度很大(\(n(n-1)/2\)根线,匹配每个点,总共\(O(n^3)\))
但是,一根直线在图像空间表达为\(y=a_1x+b_1\),这里引入参数空间,即将参数和变量的地位调换,得到
\[
b_1 = xa_1-y
\]
对于两个点\((x_1,y_1), (x_2,y_2)\),其在直线\(y=a_1x+b_1\)上的充要条件就是在参数空间内,直线\(b=x_1a-y_1,b=x_2a-y_2\)相交于\((a_1,b_1)\)
也就是图像空间共线等价于参数空间共点
不过还有一个问题,无法表达形如\(y=a,x=b\)的直线,故采用极坐标形式(非传统极坐标)
\[
\rho = x\cos\theta +y\sin\theta
\]
共线的充要条件没有改变
霍夫变换就是将参数空间划分为累加单元,\(\theta\in[-90^\circ, 90^\circ], \rho\in[-D,D]\),其中\(D\)是图像的对角线长度
- 初始直线上的点计算矩阵\(A=0\),\(A\)是累加器,用于统计每个点经过的次数,次数最大的点是最接近的直线参数
- 对图像上的所有边缘点\((x_k,y_k)\),遍历\(\theta\),计算\(\rho = x_k\cos\theta+y_k\sin\theta\)
- 若使用\(\theta_q\)得到了\(\rho_p\),那么将\(A(p,q) +=1\)
- 最终\(A(p,q)\)表示由参数\(\rho_p,\theta_q\)确定的直线上的点的个数,显然越大的参数越接近真实的直线
理论上,霍夫变换可以扩展到任何形如\(g(v,c)=0\)的函数,其中\(v\)是坐标向量,\(c\)是系数向量
霍夫变换的抗噪声能力特别强,在信噪比低的情况下能识别出曲线;缺点是首先需要二值化、边缘检测等预处理,会损失原图信息
5.3 区域内相似性
5.3.1 阈值处理
阈值的选取需要根据直方图进行,当阈值\(T\)适用于全图时,是全局阈值处理;当\(T\)在一幅图上改变时,是可变阈值处理
基本全局阈值迭代算法
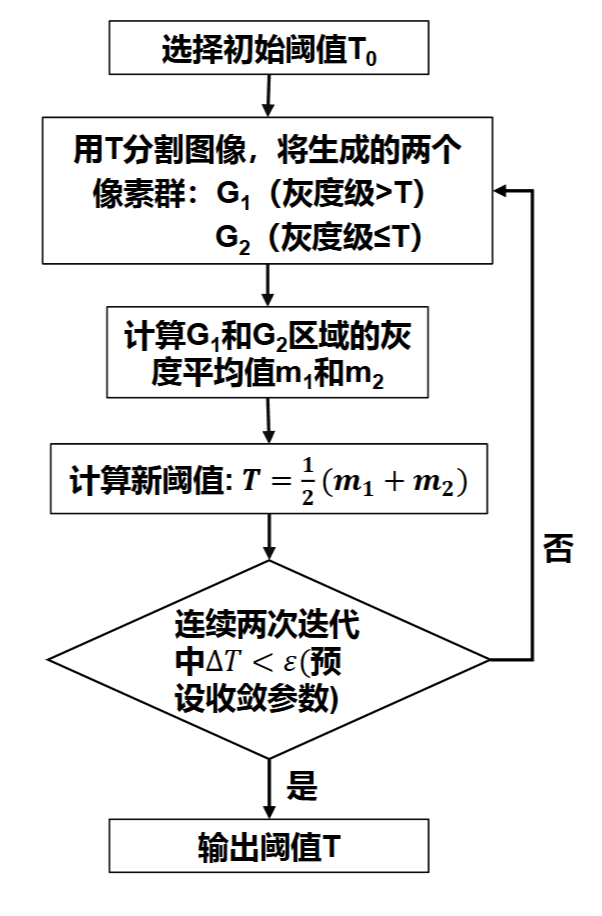
其中\(\Delta T = |T^{'}-T|\),将一次迭代中的新阈值记为\(T^{'}\),迭代的过程就是\(T=T^{'}\)(赋值)
一般初始值为整幅图像的平均值,迭代算法的收敛速度较慢
最大方差最佳全局阈值选取法(Otsu)
体现出区域内部的相似性和不同区域之间的差异性
以分为两组为例,设阈值为\(K\),步骤如下
- 计算归一化直方图,即纵坐标是占比\(p_i\)
- 计算阈值划分开的区间的占比累和\(P_1(K)=\sum\limits_{i=0}^Kp_i, P_2(K)=1-P_1(K)\)
- 计算所有区域的均值\(m_G=\sum\limits_{i=0}^{L-1}ip_i\),其中\(L\)是灰度级
- 计算各个区域的均值\(m_1=\frac{1}{P_1}\sum\limits_{i=0}^{K}ip_i, m_2=\frac{1}{P_2}\sum\limits_{i=K+1}^{L-1}ip_i\)
- 计算类间方差,也就是几个类之间的方差,\(\sigma^2_B(K)=\sum P_i(m_i-m_G)^2=P_1P_2(m_1-m_2)^2=\frac{(m_GP_1-m)^2}{P_1(1-P_1)}\),其中\(m=\sum\limits_{i=0}^Kip_i\)
- 获得的类间方差取最大值,即\(\sigma_B^2(K)=\max\limits_{0\leq K\leq L-1}\sigma^2_B\),若极大值不唯一,则取\(K=avg\{k_i\}\)
- 计算全局方差\(\sigma_G^2=\sum\limits_{i=0}^{L-1}(i-m_G)^2p_i\),注意是全体方差,计算可分离测度\(\eta^*=\frac{\sigma_B^2(K)}{\sigma_G^2}\)
几个tips
- 对于存在很强的噪声,以至于直方图没有明显的多个峰的图像,可以先用平滑滤波器处理,再用otsu
- 当目标与背景面积相差很大时,直方图没有明显的双峰/峰的大小相差很大,这时分割效果不好,即使用了平滑滤波
边缘信息改进全局阈值处理
当峰相差很大时这么干
- 计算原图\(f(x,y)\)的梯度幅度或Laplace绝对值获取边缘信息
- 规定阈值\(T\)对边缘图像处理得到\(g_T(x,y)\)
- 用\(g_T(x,y)\)的直方图计算\(K\)
- 将\(K\)代入原图,分割\(f(x,y)\)
Otsu多阈值处理
将灰度分为\(k\)类\((C_1,C_2,\ldots, C_k)\),计算\(P_i, m_i\),计算相邻区域之间的差异性\(\sigma_B^2(K_1,K_2,\ldots, K_{k-1})=\sum\limits_{i=1}^kP_i(m_i-m_G)^2\)
将\(\sigma_B^2\)对\(K_i\)求偏导取极值,得到\(k-1\)个\(K\)的值,注意只有\(k-1\)个阈值
局部分区阈值处理
局部图像中的背景与目标尺寸相当,否则会出现tips2的情况,需要再细分
根据局部图像性质的可变阈值处理
阈值的选取根据局部的统计值来改变,即
\[
Q(x,y) =
\begin{cases}
1\,\,\,\,\,, f(x,y)>a\sigma_{x,y},f(x,y)>bm_{x,y}\\
0\,\,\,\,\,, o.w.
\end{cases}
\]
其中\(\sigma_{x,y},m_{x,y}\)表示以\((x,y)\)为中心的领域的方差和均值,有时可以用全局均值代替局部均值
基于移动平均的可变阈值处理
当目标尺寸相比图像大小较小时,移动平均的可变阈值处理效果较好,处理速度比较快
就是用一个点的行区域的均值作为阈值来处理这个点
常用于打印或手写图像的分割,尤其在不均匀光照下,手写字体灰度极低,用平均准而且快
阈值处理的缺点
- 分类太简单,无法准确地分割类内方差较大的目标
- 没有完全利用图像信息,直方图完全就没有利用像素的空间分布,导致分割结果易被噪声干扰
5.3.2 区域分割
主要分为区域增长法和区域分离与聚合
区域增长法
- 确定一组能正确代表所选区域的种子(手动选)
- 确定包括相邻像素的规则(生长/相似规则)
- 指定生长停止的条件
区域分离与聚合
从整个图像开始不断分裂,得到各个区域,然后聚合这些小区域
令\(Q(R)\)表示在\(R\)中的所有像素有相同的灰度值1
- 对整幅图,进行判定,\(Q(R)\)不成立,则水平竖直分为4等分
- 对每一个子图进行步骤1,
- 对相邻的区域\(R_i,R_j\),如果\(Q(R_i\cup R_j)\),将二者聚合为一个,即使大小不一样
- 重复3直到不能聚合
当然\(Q(R)\)可以用别的谓词逻辑\(P(R)\)替换
5.3.3 聚类分割
先对数据进行标准化
\[
Z_f = \frac{x_f-\mu}{\sigma}
\]
聚类分割有很多,这里只看k-均值聚类算法
随机选取k个初始聚类中心
计算每个样本到各个中心的距离,将每个样本归类到最近的中心
这里的距离也是需要选择的,不一定是欧氏距离
对每个簇,以所有样本的均值作为新的聚类中心
重复2,3,直到中心不再变化或达到规定步骤