4 形态学

基本想法

用具有一定形态的结构元素去度量和提取图像中的对应形状，为了识别和分析

4.1 集合论

补集：记为\(A^c=\{w|w\notin A\}\)

差集：\(A-B=A\cap B^c = \{w|w\in A \and w\notin B\}\)

平移：将集合B的原点平移到\(z=(z_1, z_2)\)，则集合B重新记为\((B)_z=\{w|w = d+z,d\in B\}\)

反射：集合B按照原点中心对称，\(\hat{B}=\{w|w=-b, b\in B\}\)

4.2 结构元

一个像素集合，没有大小和形状限制，但必须有原点（可以任意位置，filter没有原点）

通常情况下假定结构元是矩阵，数值是逻辑0/1，原点是中心点

在形态学运算中，只关心结构元的前景（1）的逻辑运算

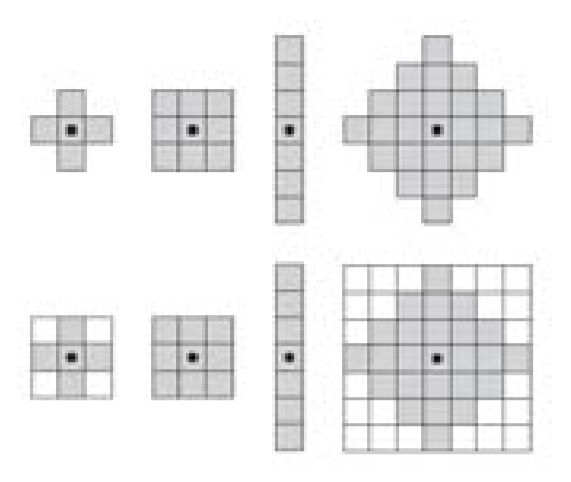
逻辑运算的结果是像素点，使用结构元的原点遍历图像的每一个像素

4.3 在二值图像中的操作

4.3.1 基本操作：适合（Fit）和击中（Hit）

适合：结构元中所有1都和图像区域重合

击中：结构元中存在1和图像区域重合

4.3.2 腐蚀

集合A用结构元B来腐蚀，记为\(A\ominus B\)，定义为
\[ A \ominus B = \{z|(B)_z\subseteq A\} \Leftrightarrow \{z|(B)_z\cap A^c = \phi\}\\ A(z)= \begin{cases} 1\,\,\,\, (B)_z \mathsf{Fits} A\\ 0\,\,\,\, o.w. \end{cases} \]
表示B移动后完全在A中，B的原点位置的集合

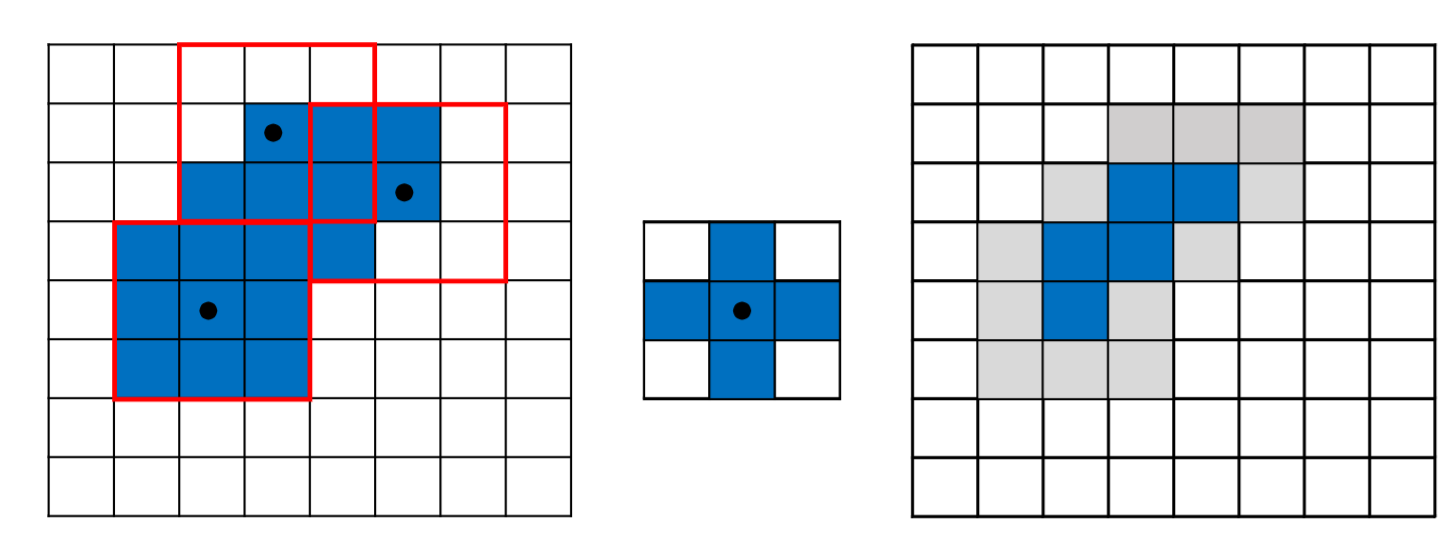
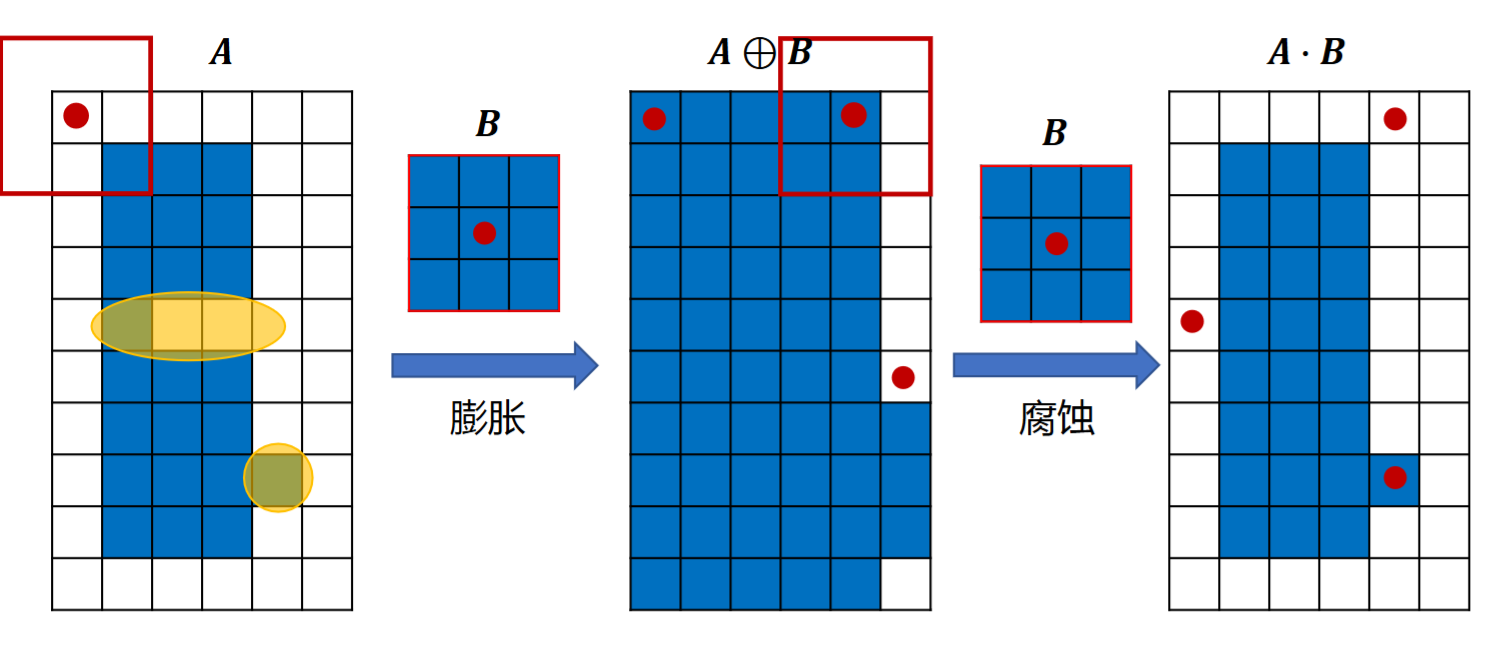
腐蚀可以消除边界点，使边界向内部收缩，可以消除小且无意义的物体

4.3.3 膨胀

集合A用结构元B来膨胀，记为\(A\oplus B\)，定义为
\[ A \oplus B = \{z|\hat{(B)_z}\cap A\neq \phi\}\\ A(z)= \begin{cases} 1\,\,\,\, \hat{(B)_z} \mathsf{Hits} \,\,\,A\\ 0\,\,\,\, o.w. \end{cases} \]
表示B的反射进行平移且与A存在非空交集，B的原点的位置的集合

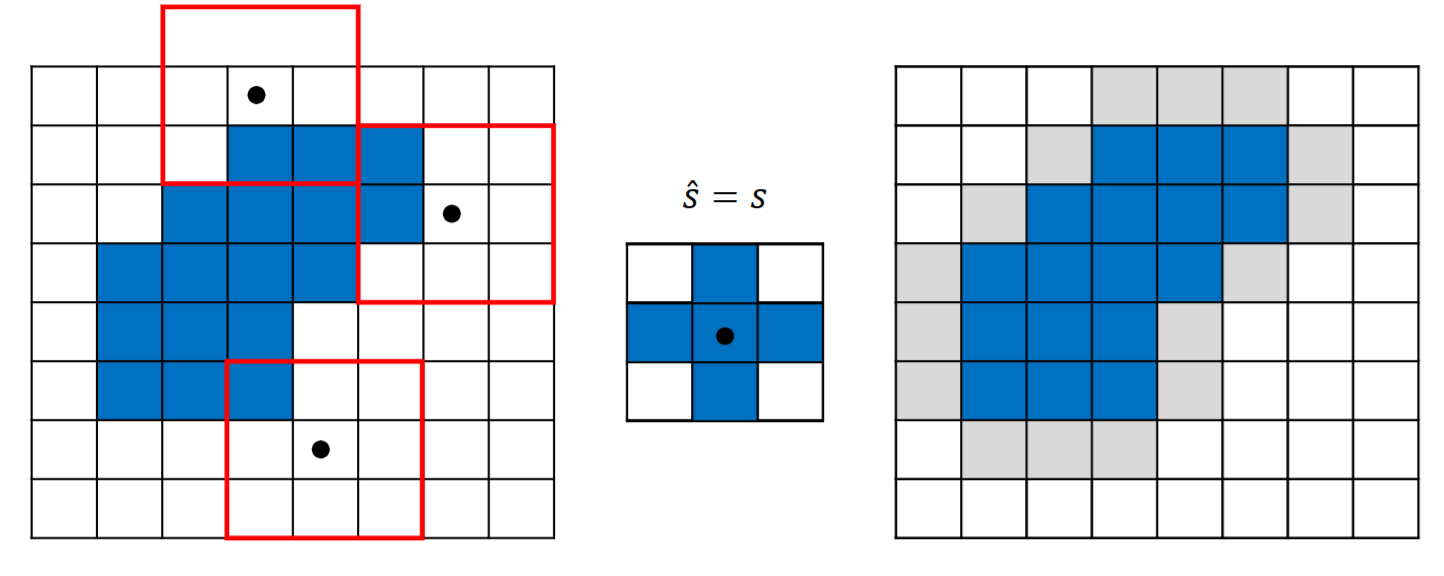
膨胀使得边界向外部扩展，增加大小，填补缺口和凹陷

4.3.4 腐蚀与膨胀的对偶性

\[ (A\ominus B)^c = A^c\oplus \hat{B}\\ (A\oplus B)^c = A^c\ominus \hat{B} \]

4.3.5 开运算

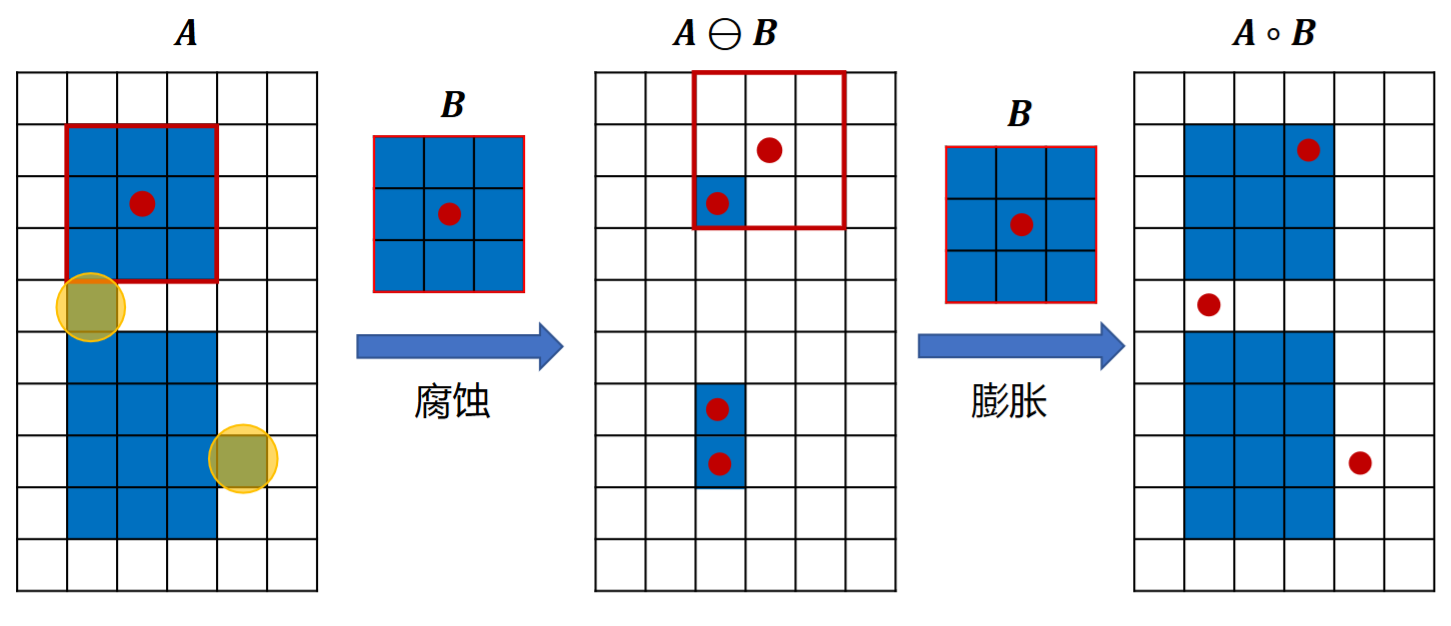
集合A用结构元B进行开运算，就是先用B腐蚀A，再对结果进行膨胀，记为\(A\circ B\)
\[ A\circ B = (A\ominus B)\oplus B \]
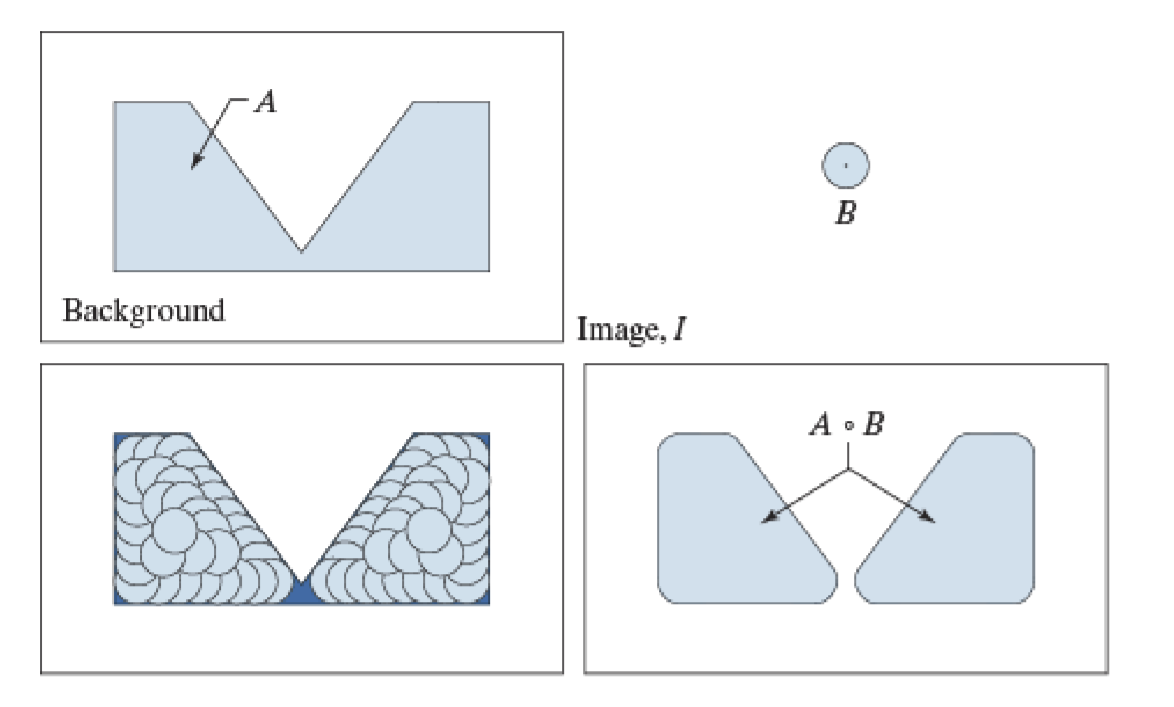
开运算能后去除孤立的小点，毛刺和小桥

几何解释

B在A边界内部转动，B中的点能达到的A的内部的最远的点，即
\[ A\circ B = \bigcup \{(B)_z|(B)_z\subseteq A\} \]
所有的平移后的结构元的集合（与原点的集合区分）

4.3.6 闭运算

结构元B对集合A做闭运算，就是先用B对A膨胀，后用B对结果进行腐蚀，记为\(A\cdot B\)
\[ A \cdot B = (A\oplus B )\ominus B \]
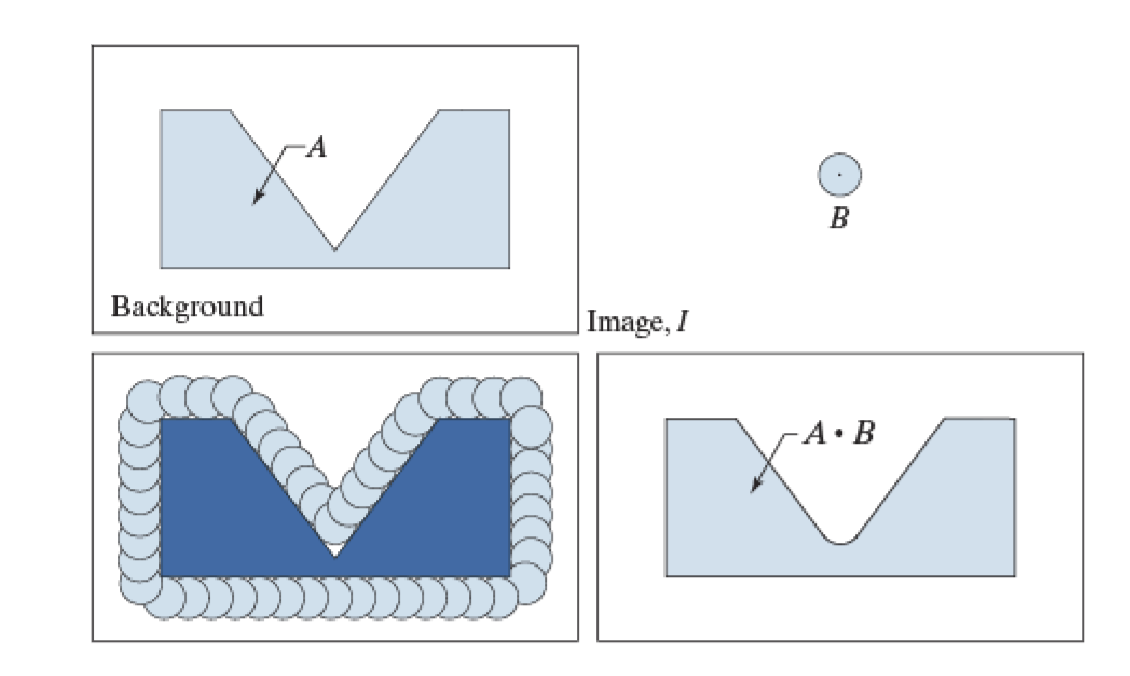
闭运算可以填补物体内细小空洞，连接临近物体

几何解释

B在A的外边界转动，B中的点能达到的A的边界的最近点

4.3.7 开运算与闭运算

1. 先开操作，构成了噪声滤波器，将小的噪声颗粒去除
2. 但是内部的一些有效性息也没了，需要闭运算进行修补

对偶性
\[ (A\cdot B)^c = A^c \circ \hat{B}\\ (A\circ B)^c = A^c \cdot \hat{B} \]

开运算性质

1. \(A\circ B \subseteq A\)
2. 如果\(C \subseteq D\)，那么\(C\circ B \subseteq D\circ B\)
3. \((A\circ B )\circ B = A \circ B\)

闭运算性质

1. \(A \subseteq A\cdot B\)
2. 如果\(C \subseteq D\)，那么\(C\cdot B \subseteq D\cdot B\)
3. \((A\cdot B )\cdot B = A \cdot B\)

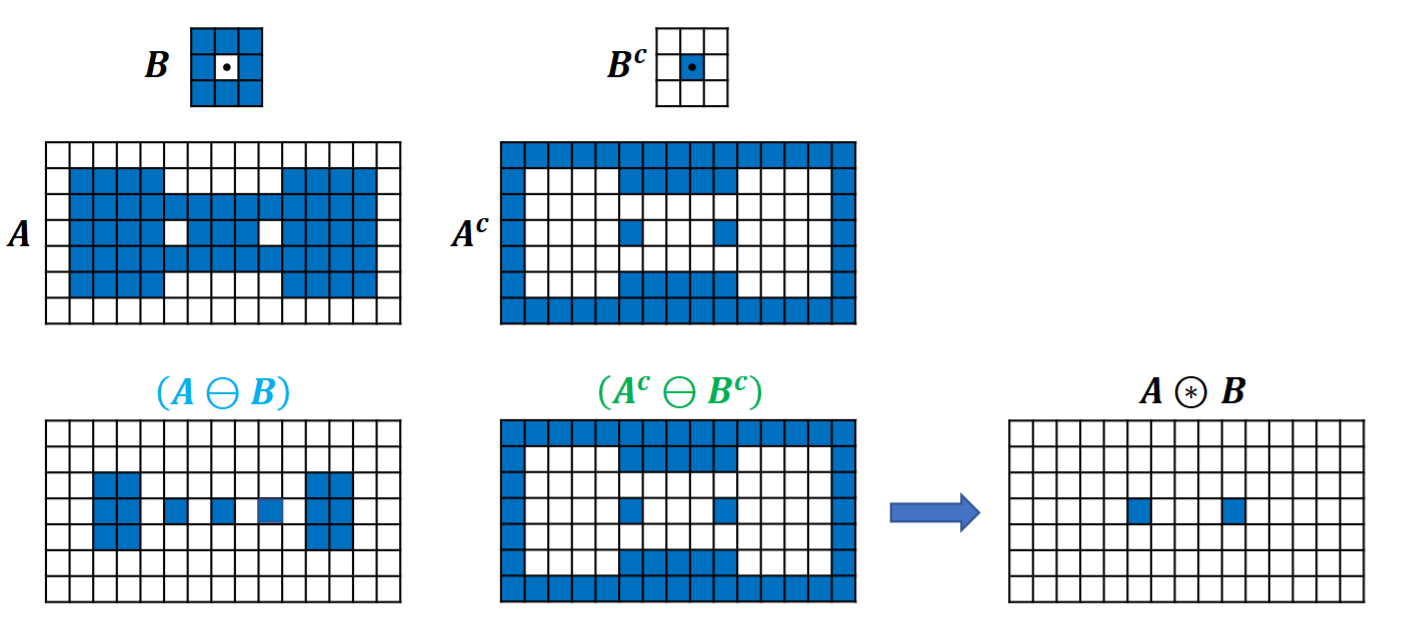
4.3.8 击中-击不中变换

定义两个结构元\(B_1,B_2\)，在前景中使用\(B_1\)进行腐蚀，在背景中使用\(B_2\)
\[ A \circledast B_{1,2} = \{z|(B_1)_z\subseteq A \and(B_2)_z\subseteq A^c \} = (A\ominus B_1)\cap(A^c\ominus B_2) \]
一般选定的\(B_1 = B, B_2=B^c\)，此时的返回结果就是A中与B一摸一样的结构的原点

4.3.9 边界提取

边界定义为\(\beta(A)\)，使用结构元B腐蚀A，然后求其与A的差集
\[ \beta(A) = A - (A \ominus B) \]
其中B是8邻接的

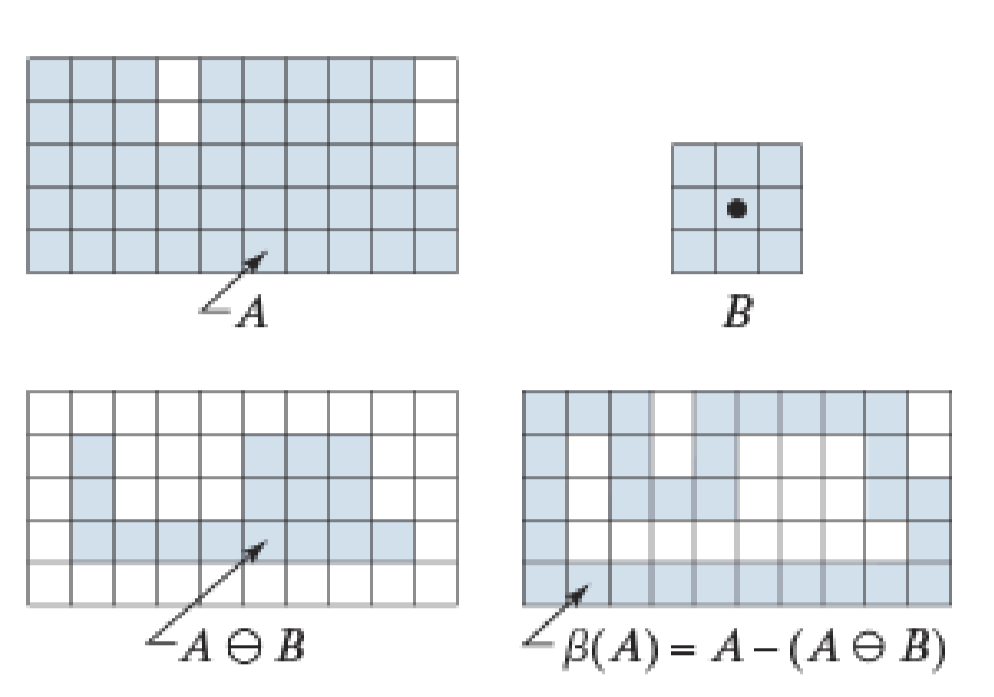
边界提取相对于锐化滤波的好处：后者通常对噪声敏感，边缘不连续不规则

4.3.10 孔洞填充

将闭合边界内部的空洞填满
\[ X_k = (X_{k-1} \oplus B) \cap A^c \]
当\(X_k = X_{k-1}\)时，停止迭代；A是原图中的一个轮廓，B是4邻接的

需要先给定一个种子点，从种子点膨胀至整个孔洞，最后与原图做并集，得到填充完的图像

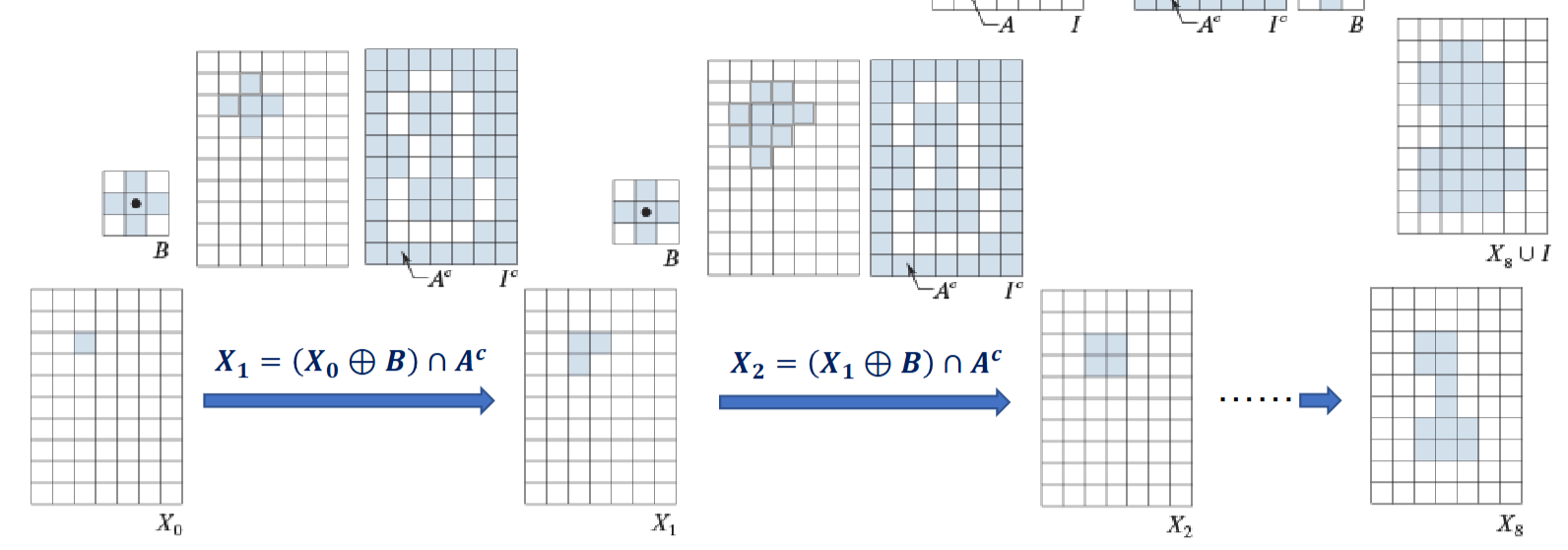
为了找出所有的孔洞，可以使用阈值变换

当边缘未闭合时，收敛次数会很大，因为背景也在填充。通过设置收敛次数的阈值，可以用来检测图像是否闭合

如何一次性找出所有的种子点？

利用白顶帽，将本就灰度低的孔洞灰度变得更低，可以认为灰度为0，然后用阈值反变换，将0变为255，得到所有的孔洞种子

但是风险也很明显

4.3.11 连通分量提取

\[ X_k = (X_{k-1} \oplus B) \cap I \]

当\(X_k = X_{k-1}\)时，停止迭代；I是原图，B是8邻接的

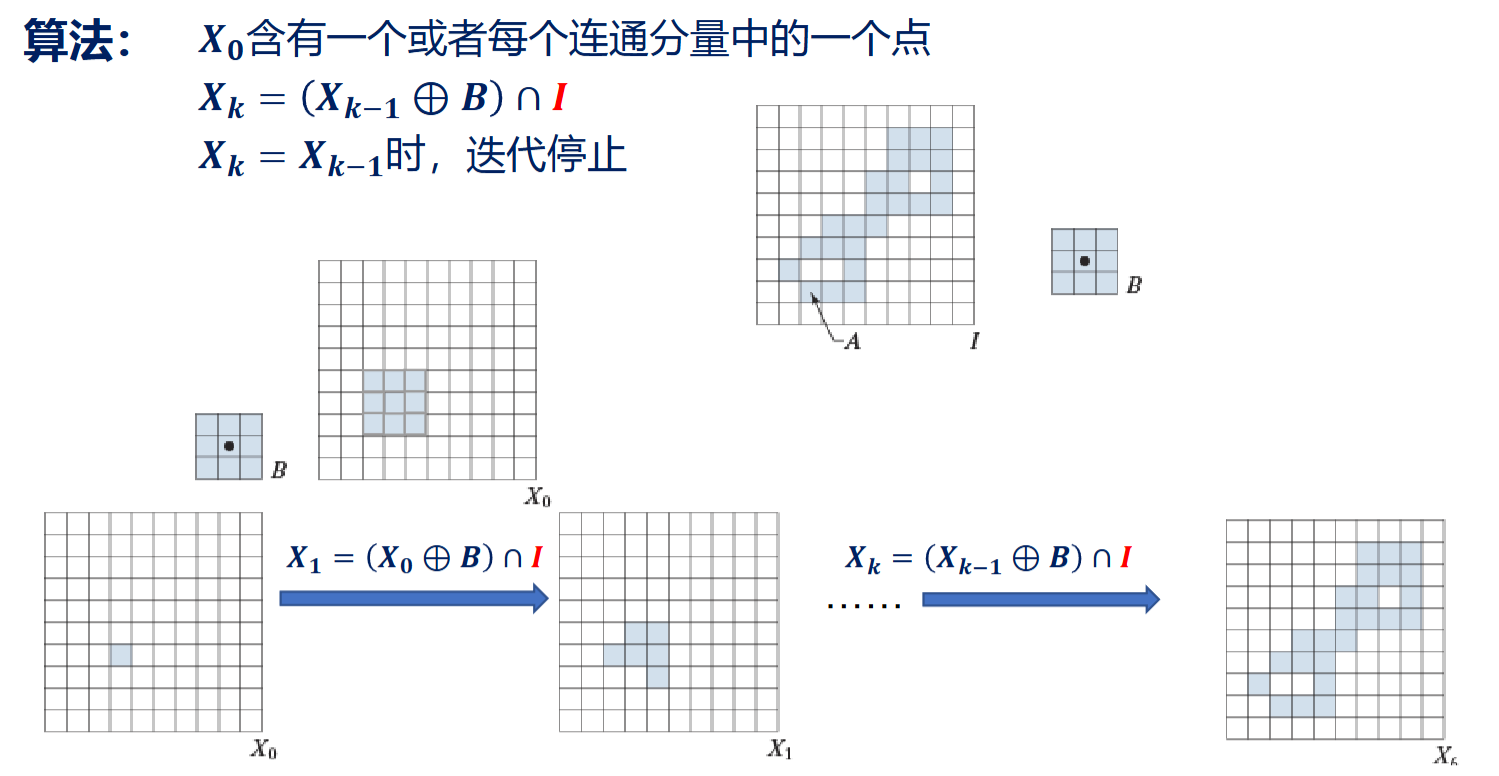
算法和孔洞填充很像，但是B和I不同

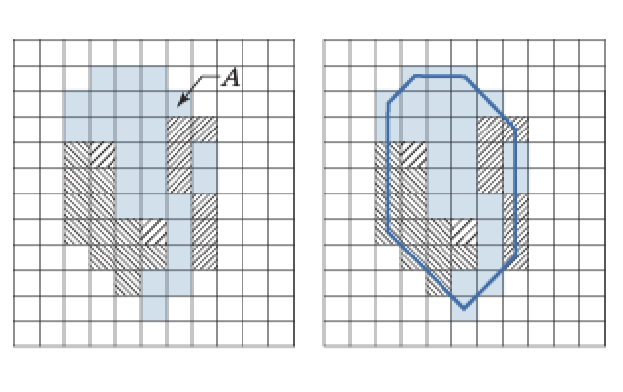
4.3.12 凸壳

一个多边形内任意两点的连线在多边形内，则称这是个凸集

集合\(S\)的最小凸集\(H\)称为S的凸集合，\(H-S\)称为凸缺

图像在采集时可能由于光照等原因发生缺损，凸壳处理可以弥补缺损

求\(A\)的凸壳\(C(A)\)的算法如下：

令\(B^i\)如下所示，其中\(\times\)表示don't care term

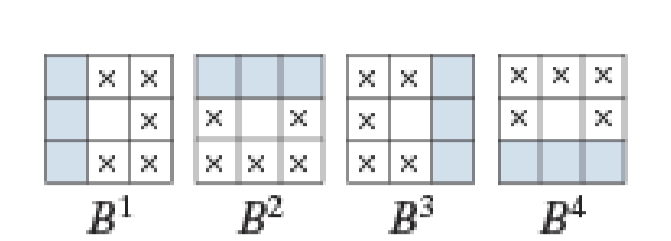
\[ X^i_k = (X^i_{k-1}\circledast B^i)\cup X_{k-1}^i \]

其中\(X^i_0 = A\)，当\(X_k^i = X_{k-1}^i\)时结束，记\(D^i = X_k^i\)，则凸壳为
\[ C(A) = \bigcup \limits_{i=1}^4 D^i \]

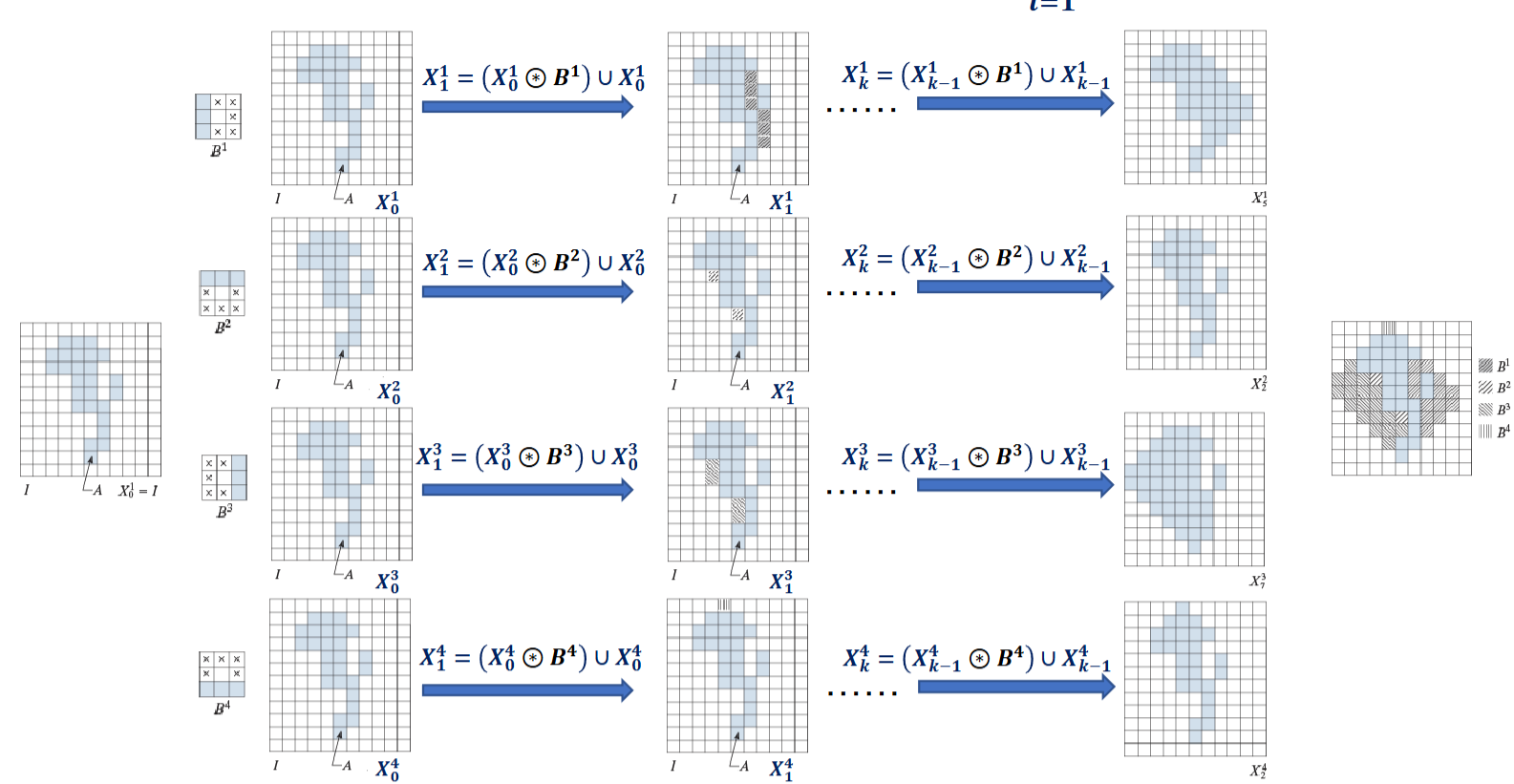
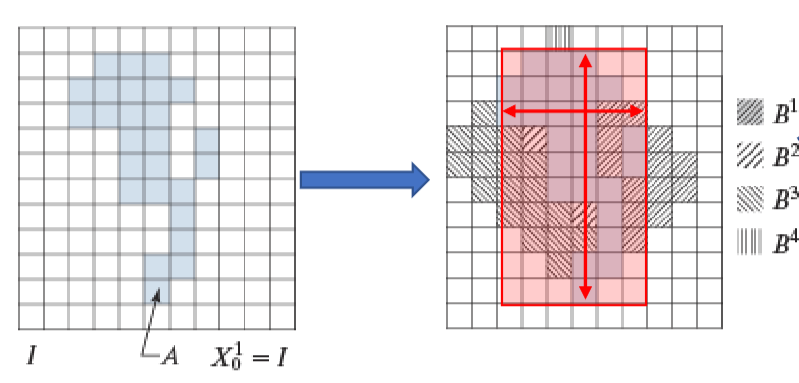
但是还没结束，这样并不是最小的，需要在水平和垂直方向上再限制大小

或者设计更精准的结构元，代价是时间复杂度更高

4.3.13 细化

细化表示为
\[ A \otimes B = A - (A\circledast B) = A\cap (A\circledast B)^c \]
定义结构元序列\(\{B^i\}\)，\(B^{i+1}\)通常是\(B^i\)的旋转，使用这个序列对\(A\)连续细化，直到\(A\)不再发生改变为止

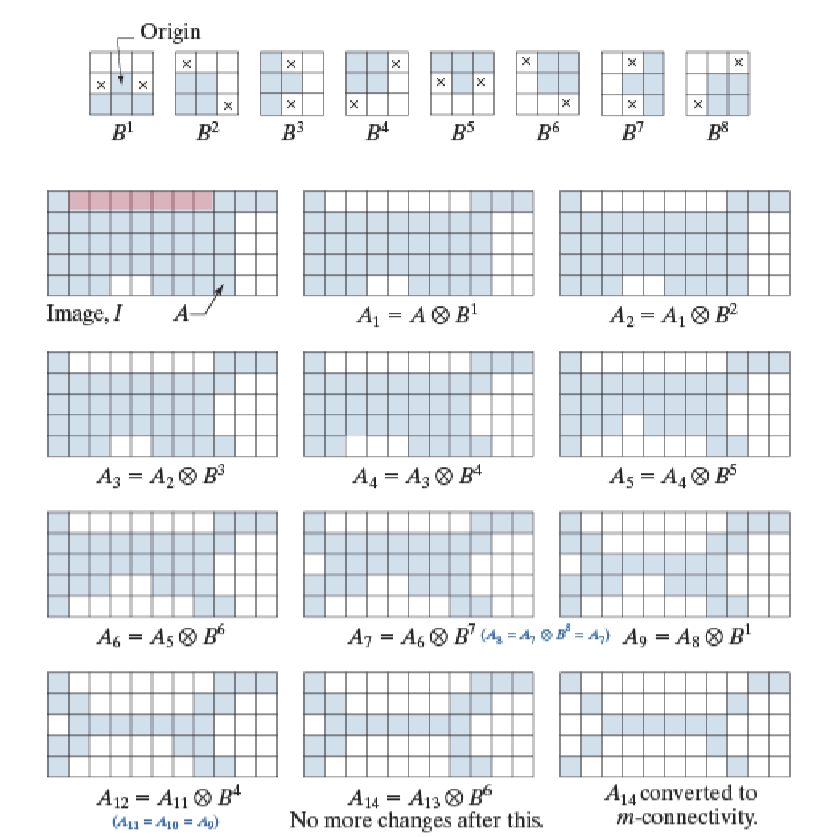
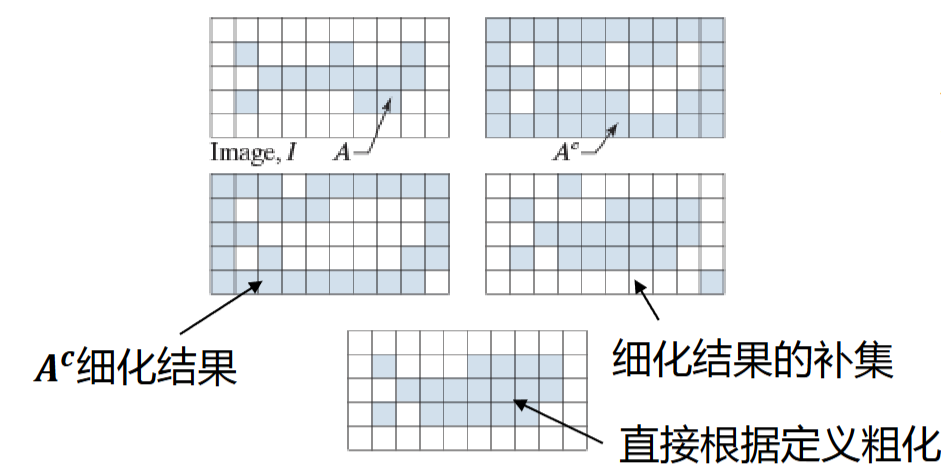
4.3.14 粗化

粗化表示为
\[ A \odot B = A\cup (A\circledast B) \]
与细化类似，可以用一系列的\(B^i\)操作

实际中通常是先对\(A^c\)细化得到\(C\)，再求\(C^c\)得到粗化的结果，不过会产生一些断点

4.3.15 骨架

角平分线

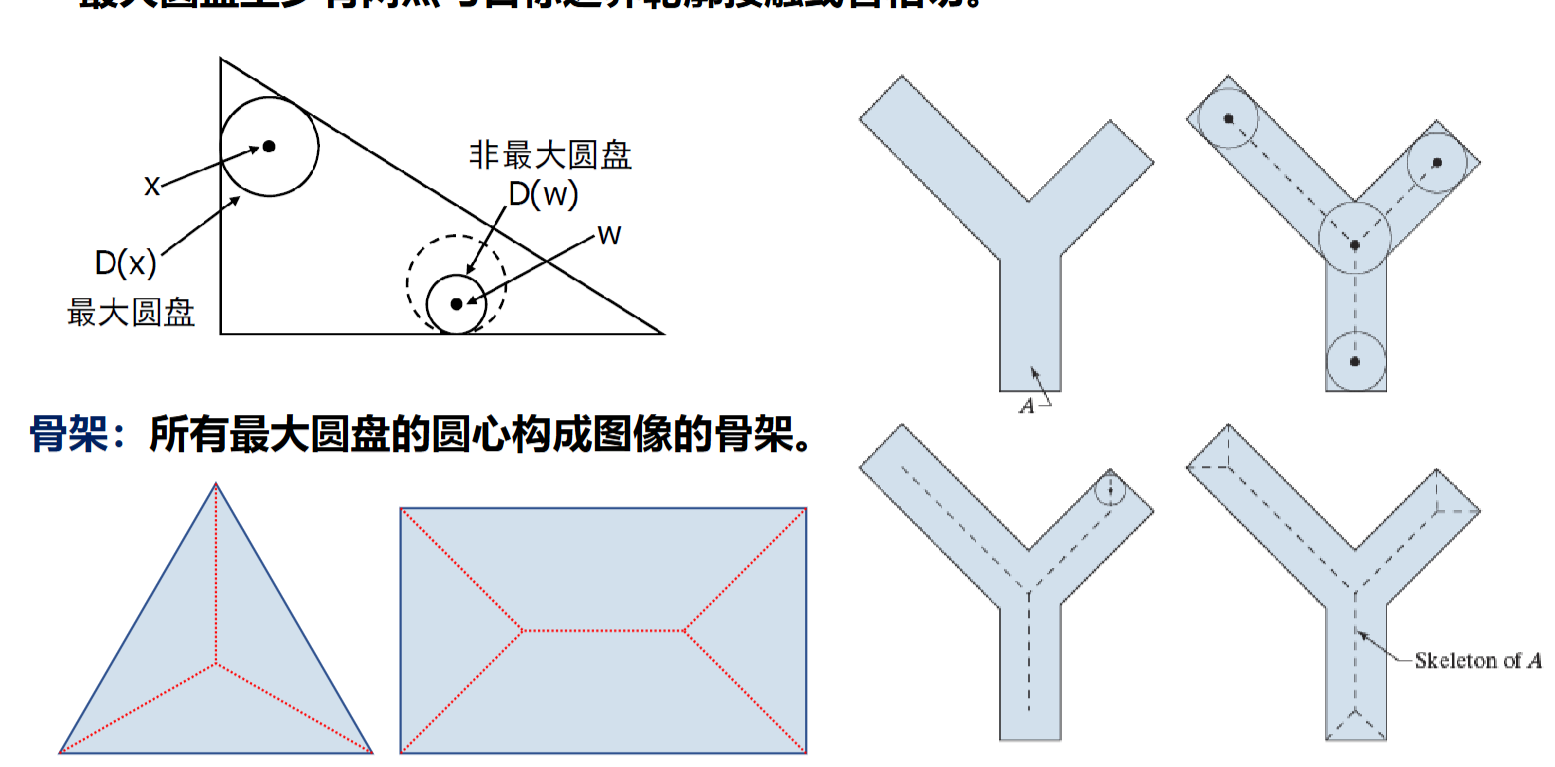
可以通过腐蚀和开运算来实现
\[ S(A) = \bigcup\limits_{k=0}^N S_k(A) \]
其中\(S_k(A)=(A\ominus kB)-(A\ominus kB)\circ B\)，\(A\ominus kB\)表示连续\(k\)次腐蚀，\(N\)是\(A\)被腐蚀为空集前最后一次迭代

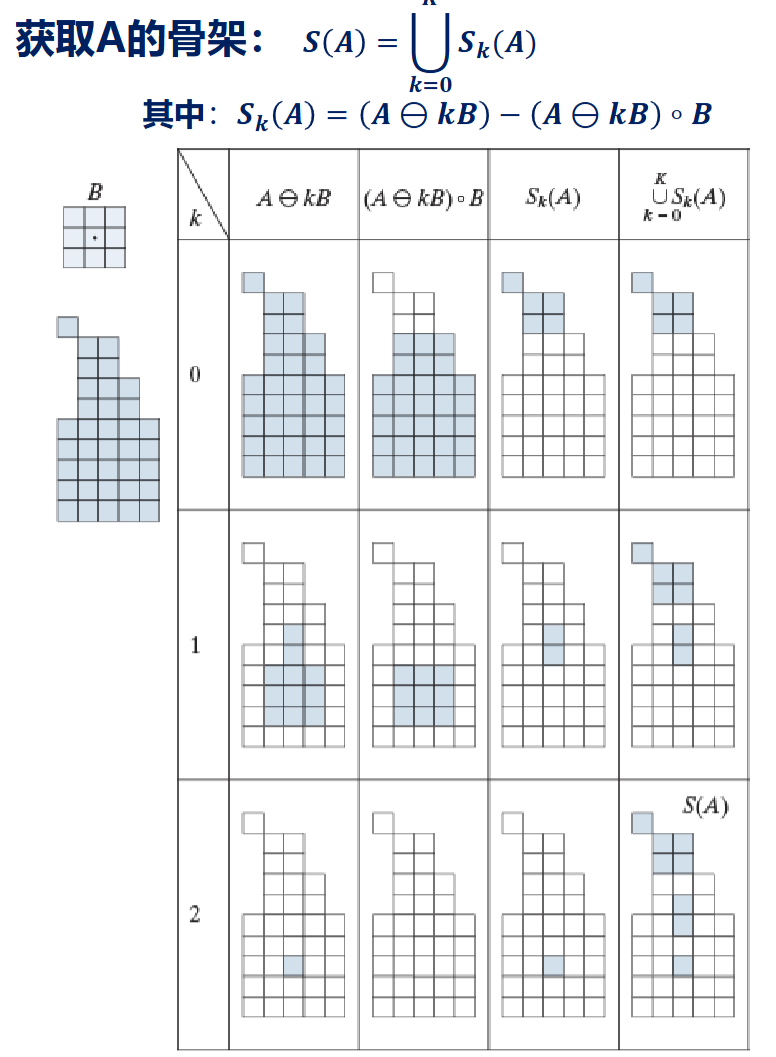
上面\(N=2\)

可以通过\(A\)的骨架的子集来重建\(A\)，注意存储的是子集
\[ A = \bigcup\limits_{k=0}^N (S_k(A)\oplus kB) \]

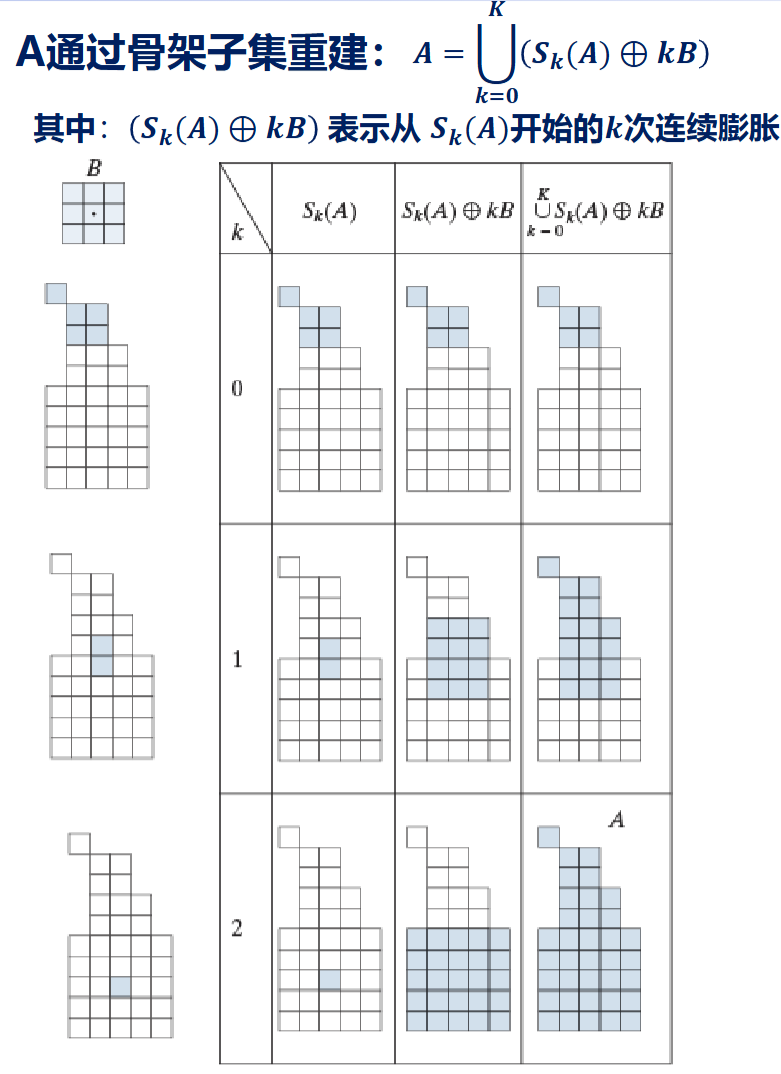
4.3.16 剪裁

是对细化和骨架化的补充

分为以下几步：

细化
\[ X_1 = A\otimes \{B\} \]
多次细化消除毛刺

寻找端点
\[ X_2 = \bigcup\limits_{k=1}^N (X_1\circledast B^k) \]
其中\(N\)是\(B^i\)的个数

膨胀，次数等于细化的次数（也就是删除的毛刺的最大元素个数）
\[ X_3 = (X_2\oplus H)\cap A \]
其中\(H\)是一个满的正方形

取并集
\[ X_4 = X_1\cup X_3 \]
得到的\(X_4\)就是目标结果

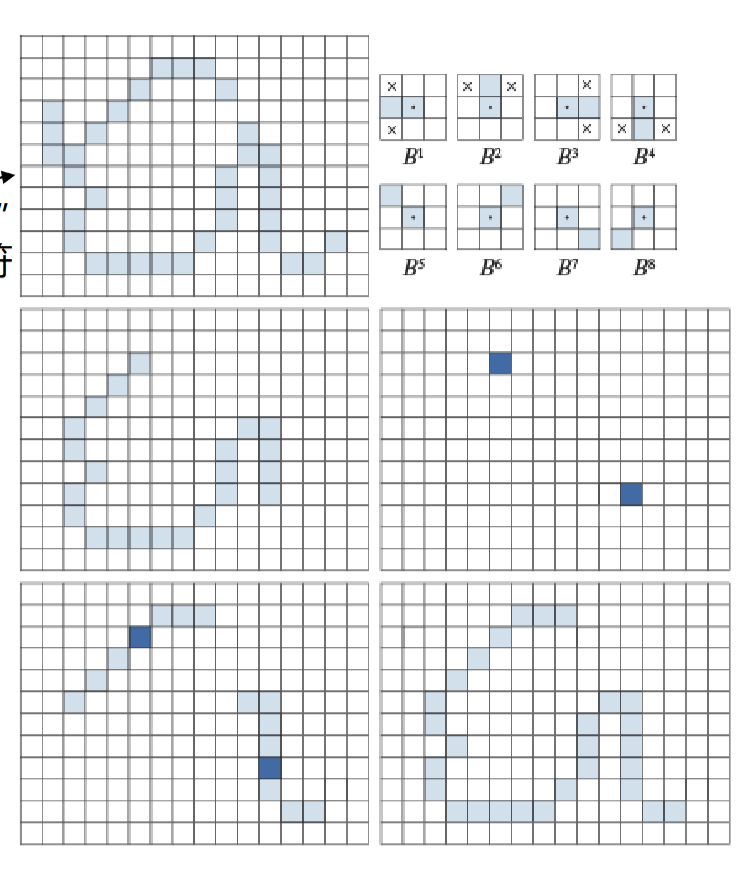
上面有3个删除的毛刺，膨胀了3次

4.4 灰度级形态学

结构元分为平坦/非平坦，前者只有0和1，后者多样

同样地，结构元存在原点，但是不同的是结构元的每一个像素值是灰度值

4.4.1 腐蚀与膨胀

对平坦结构元\(b\)，当其原点位于\((x,y)\)时，腐蚀和膨胀分别如下，也就是这个范围内灰度的极值
\[ [f \ominus b](x,y) = \min\limits_{(s,t)\in b}\{f(x+s,y+t)\}\\ [f \oplus b](x,y) = \max\limits_{(s,t)\in b}\{f(x-s,y-t)\}\\ \]
\("-"\)产生自对b的中心对称

对非平坦结构元，定义为
\[ [f \ominus b](x,y) = \min\limits_{(s,t)\in b}\{f(x+s,y+t)-b(s,t)\}\\ [f \oplus b](x,y) = \max\limits_{(s,t)\in b}\{f(x-s,y-t)+\hat{b}(s,t)\}\\ \]
其中\(\hat{b}(x,y) = b(-x,-y)\)，一一对应相加减

对偶特性依然在
\[ [f\ominus b]^c = f^c\oplus \hat{b}\\ [f\oplus b]^c = f^c\ominus \hat{b} \]
其中\(f^c(x,y) = -f(x,y)\)

一般腐蚀后更暗，膨胀后更亮

4.4.2 开闭运算

定义同二值图像

满足
\[ [f\circ b]^c = f^c\cdot \hat{b}\\ [f\cdot b]^c = f^c\circ \hat{b} \]
几何解释如下

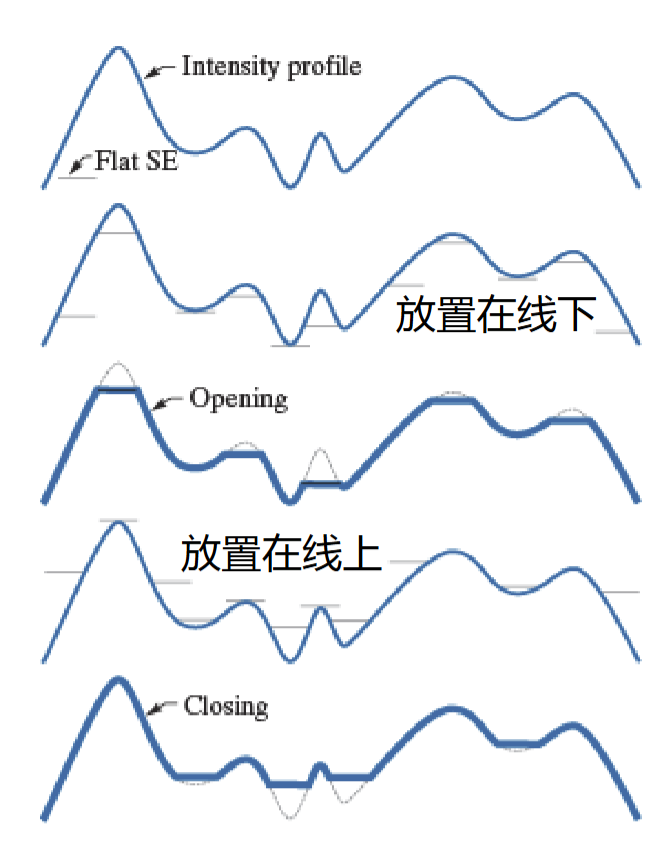
这是一维的灰度刨面图，开运算就是从下方削去峰值，闭运算就是从上方填平谷值

红字的\(f\)改为\(r\)

开运算对图像的暗特征和背景的影响忽略不计，但亮特征变小；闭运算相反；效果取决于结构元大小

开闭运算的组合可以产生形态学滤波器进行平滑和去噪

4.4.3 形态学梯度

定义
\[ g = (f\oplus b)-(f\ominus b) \]
为灰度图像的形态学梯度，其中\(b = I_{3\times 3}\)，原点在中心

4.4.4 顶帽变换和底帽变换

白顶帽变换和黑底帽变换分别是
\[ T_{hat}(f) = f - (f\circ b)\\ B_{hat}(f) = (f \cdot b) -f \]
白顶帽可以获取大的亮特征，除去暗特征

黑底帽可以获取大的暗特征，除去亮特征

一个重要应用是矫正不均匀光照的影响，进行阈值处理之前先进行对应的帽变换

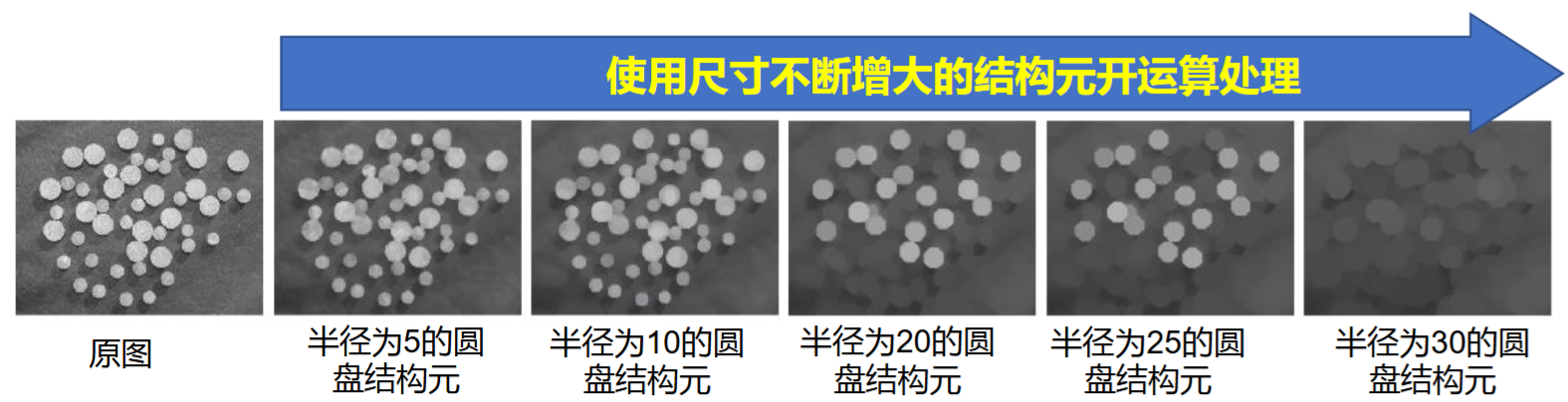
4.4.5 粒度测定

特殊大小的开运算会对包含类似大小颗粒的区域产生最大影响，用不同大小的结构元对图像进行开运算，除去的就是类似大小的结构，可以进行粒度的检测和统计

4.4.6 纹理分割

如何一步一步得到右边的图像：

1. 选用小结构元进行闭运算，得到第二张图
2. 用很大的结构元进行开运算，得到第三张图
3. 对第三张图进行形态学梯度变换得到纹理边界，将边界叠加到原图上得到第四张图