3 图像增强
定义:使图像比处理前更适合一个特定的应用
图像增强:不估计图像退化过程,求得平均图像质量改进
图像复原:估计图像退化过程,有点像逆过程
空间域图像增强
空间域内将一个灰度区间映射到另一个灰度区间:\(g(x,y)=T[f(x,y)]\),T为在(x,y)邻域上定义的算子
1x1的邻域算子:点运算增强
全图像邻域算子:直方图处理
mxn邻域算子:空间滤波
3.1 点运算增强
改变某一位置的灰度值,与像素位置无关,即:\(s=T[r]\),其中r是原灰度,s是变换后灰度
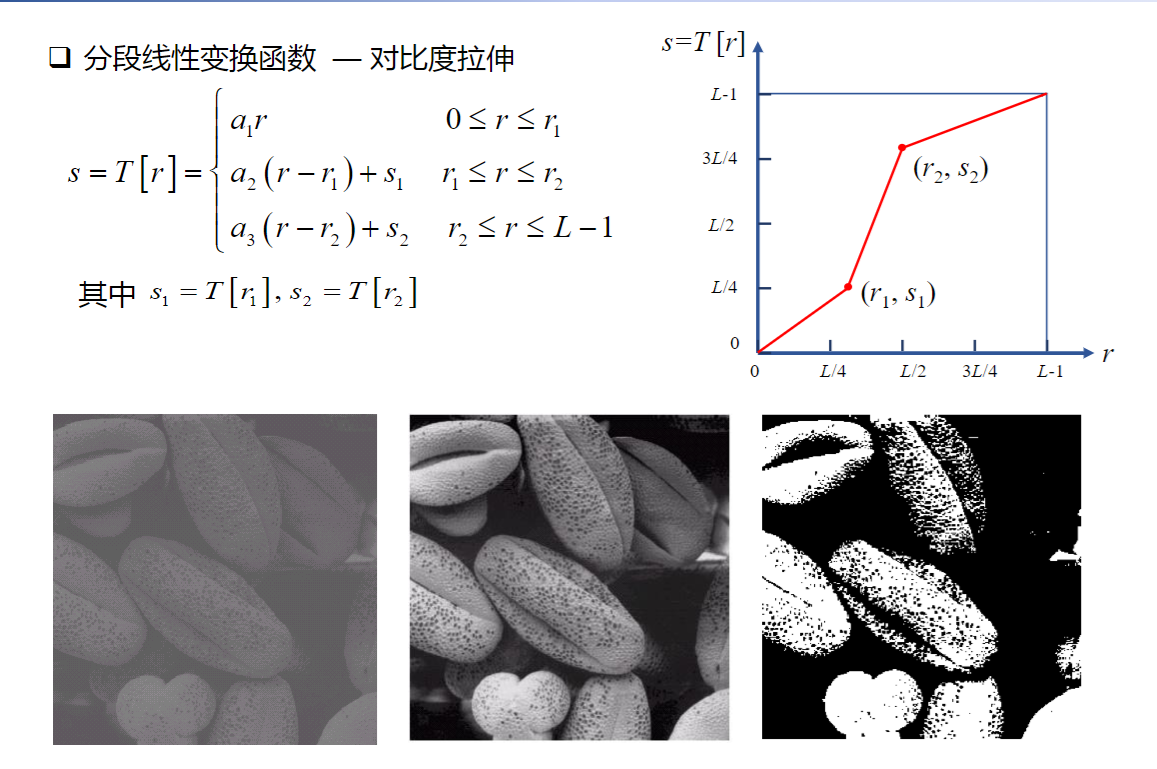
常见的点运算增强函数
阈值处理函数
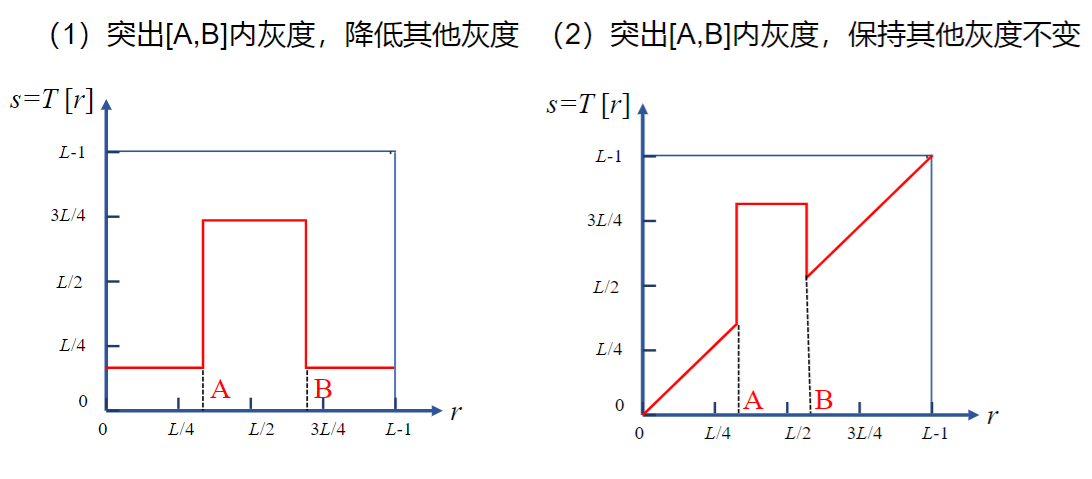
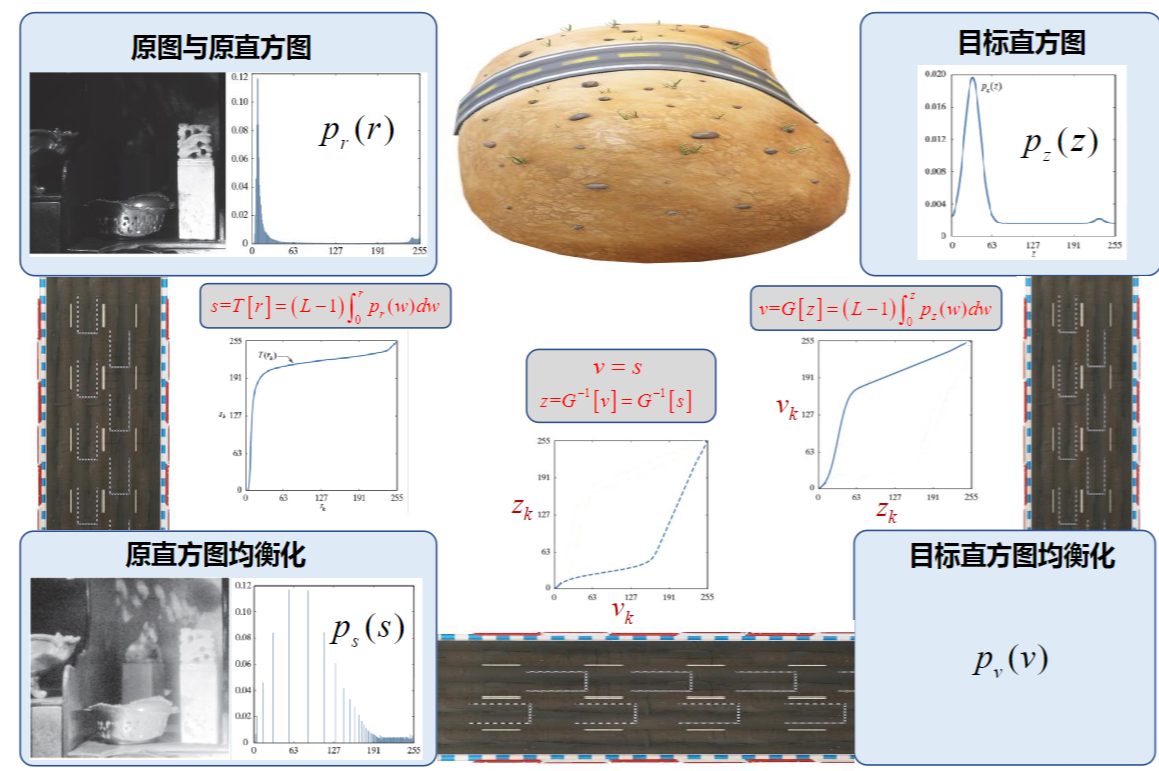
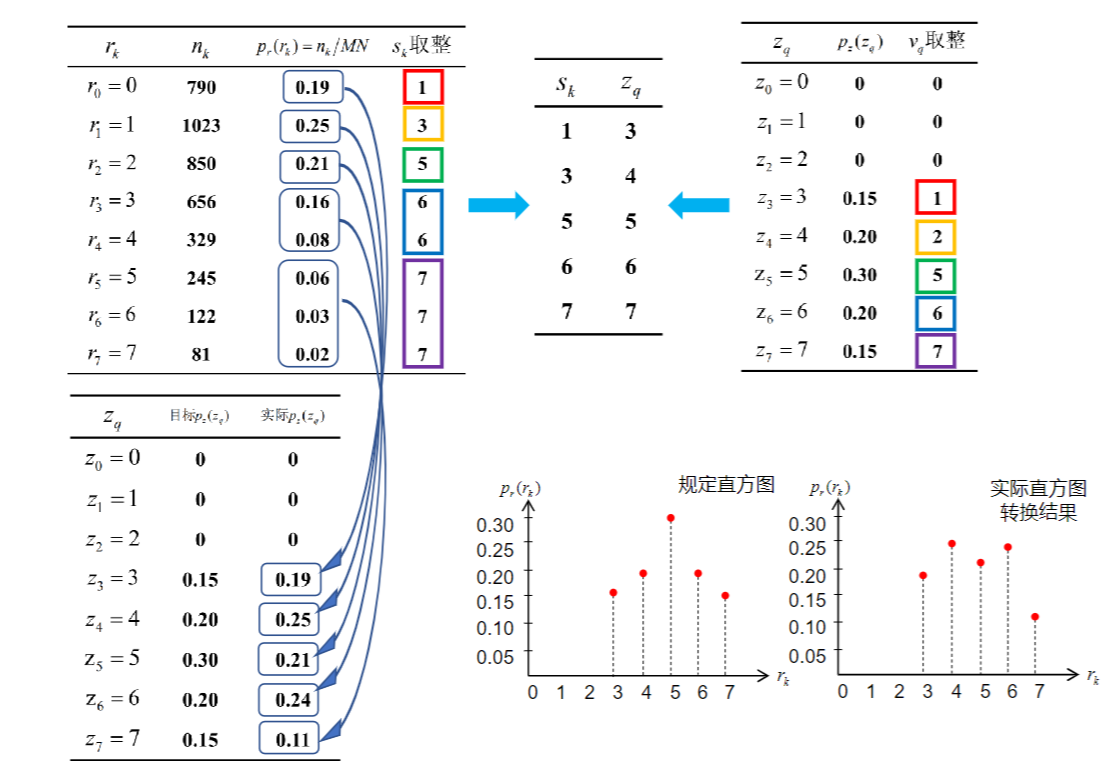
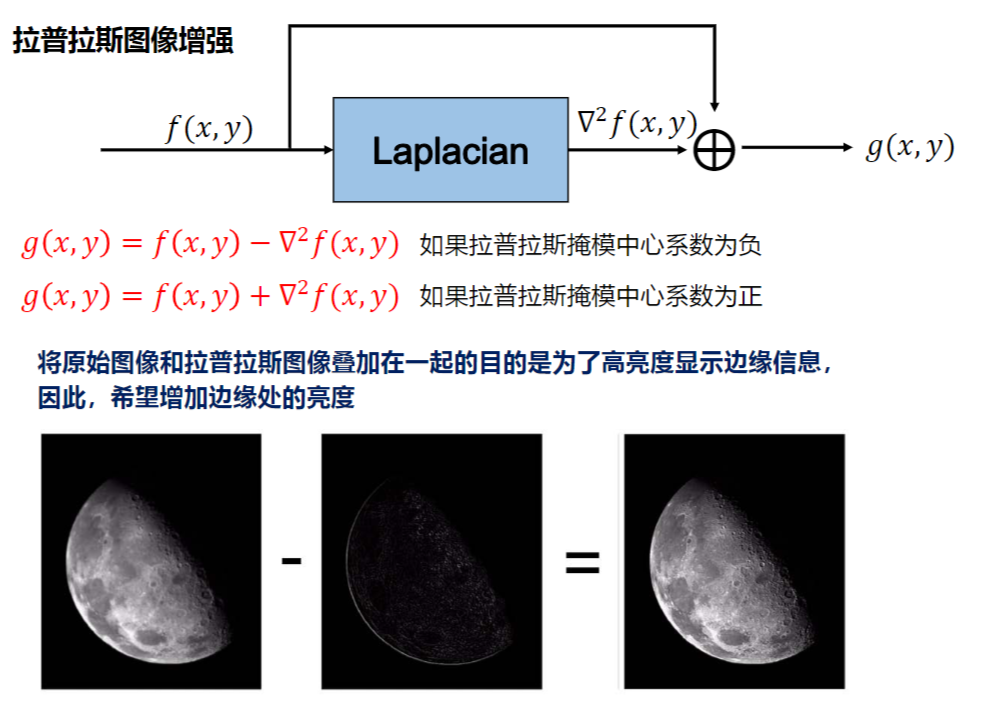
增强图像轮廓 灰度反转函数 对数变换函数 典型应用:图像的傅里叶频谱范围很广,压缩高频噪点,可以显示低频信息 幂律变换函数 应用最广泛;让太暗的图像变亮,γ<1 分段线性变换 一个分段的线性函数,可以拉伸对比度 灰度级分层 比阈值处理函数灵活 比特平面分层 用二进制表示灰度,将一张图分成8张图,按位显示 灰度直方图:图像中某一灰度的像素个数的分布情况,只反映灰度的分布,不反应图像位置 一幅图像的各个子区域的直方图之和等于全图的直方图 PDF:\(P_r(r_k)=\frac{n_k}{\sum n}\) ; CDF:\(F_r(r_k)=\sum\limits_{i=0}^k P_r(r_i)\) 一般来说,像素占据整个灰度级且分布均匀的图像,将具有高对比度和多种灰色调,最好看细节 将一副图像处理成上述样子的过程,为直方图均衡化 目标 CDF:\(F_r(k)=\int_0^k{p_r(r)dr}\),\(F_s(k)=\int_0^k{p_s(s)ds}\) 为了防止黑白颠倒,\(T[\cdot]\)应该是一个单增函数,即对任意的k,都有\(F_r(k)=F_s(k)\)(极端反例,黑色变得比白少,图像变白了) 得到\(p_r(r)dr=p_s(s)ds\Rightarrow ds=(L-1)p_r(r)dr\Rightarrow s=(L-1)\int _0^r p_r(w)dw\) 对于数字图像,灰度级离散,有\(s_k=[T(r_k)]=[(L-1)\sum\limits_{j=0}^k p(r_j)]\),一般四舍五入 由于取整操作的存在,直方图均衡化不是线性操作,可能引起灰度级数变化和图像细节损失 不同图像经过直方图均衡化后的直方图类似,直方图均衡化不需要输入任何参数 优点:能自动增强图像的对比度 缺点:灰度级减少,细节损失;存在高峰的直方图,处理后不自然;结果唯一不能交互 目标:修改直方图,使其与事先预定的直方图匹配 方法 由于取整操作,存在一定偏差 对图像的小细节增强,在图像的每一个像素的邻域中,根据灰度级分布设计变换函数,进行直方图规定化 机制:输出图像中每一点关于相关区域的映射,实质是相关/卷积运算 空间滤波器又称掩膜,窗口,核,模板(Spatial Kernel) 模板中的值是无量纲的 滤波器的形状和大小没有规定,不需要一定是矩阵,没有原点 对于一个mxn,中心坐标为(0,0)的模板w(s,t),定义以下运算 相关运算 卷积运算 一般模板是中心对称的,此时相关运算与卷积运算一致 很显然空间滤波后,原图的边界无法被映射 一副MxN的图,经过mxn的模板处理后,得到的图像大小是\([M-(m-1)][N-(n-1)]\) 处理图象时要说明边界处理的方法 舍弃边缘像素点 图片变小 边缘外圈补零 用0灰度补边缘,看起来就是多了一圈黑框 边缘外圈补边缘点像素 分为三种补法:重复(replicate),对称(symmetric),循环(cirular) 图像识别 不是中心对称的图像,要用相关运算,不能用卷积运算(会先中心对称一次,识别不了) 按数学形态 按处理效果 平滑--求和平均(积分);锐化--微分差分(梯度) 常见噪声分类 平滑线性滤波器 分为盒状滤波器和加权平均滤波器 前者所有的系数相同,采用邻域均值法;后者依据像素的重要性赋予权重 注意为了防止灰度值溢出,需要对滤波器进行归一化、 盒状滤波器 半径越大,信噪比提升越大,平滑效果越好,但是图像更模糊 优点:算法简单,速度快 缺点:在边缘和细节处模糊 加权平均滤波器 重点在于选择参与平均的点数和各点的权重;待处理的点和离它越近的点权重越大 优点:保留了边缘细节 平滑非线性滤波器 主要是中值滤波器,它对滤波脉冲干扰和颗粒噪声(如椒盐噪声)很有效,在消除噪声的时不会/小程度边缘模糊 但是对一些细节多(点/线/尖顶)的图像,不能用中值滤波 在医学图像中,病灶一般符合细节特点,故医学图像不能中值滤波 平滑滤波器小结 梯度运算 一阶差分:\(\frac{\part f}{\part x}=f(x+1,y)-f(x,y)\) 二阶差分:\(\frac{\part^2 f}{\part x^2}=[f(x+1,y)-f(x,y)]-[f(x,y)-f(x-1,y)]=f(x+1,y)+f(x-1,y)-2f(x,y)\) 一阶差分对灰度阶梯有较强响应,会产生较宽的边缘 二阶差分对细节有较强响应,对灰度阶梯产生双响应 二阶的处理比一阶好(细节),一阶主要提取边缘 拉普拉斯算子 以上是水平竖直的差分,也能定义斜的差分 当α取0,表示水平竖直;当α=1,表示斜向 所有的Laplace算子模板,其数值之和恒等于0 拉普拉斯增强 可以增加边缘的亮度,注意正负号 有锐化作用 由于Laplace算子存在负数,在处理后可能出现负的灰度,一般有两个处理 \(g(x,y)=f(x,y)+\nabla^2f(x,y)\),α=0时的算子 钝化掩蔽 也叫非锐化掩蔽 记\(\overline f(x,y)\)为原图的平滑处理,则\(g_{\mathsf{mask}}(x,y)=f(x,y)-\overline{f}(x,y)\)为锐化模板(损失低频,保留高频) 最终得到\(g(x,y)=g_{\mathsf{mask}}(x,y)+f(x,y)\) 梯度增强 存在负值和溢出 利用梯度算子的模量\(M(x,y)=|\nabla f(x,y)|=\sqrt{f_x^2+f_y^2}\) 由于这个运算很耗时,用近似处理 \(\sqrt{f_x^2+f_y^2}=\sqrt{(f(x+1,y)-f(x,y))^2+(f(x,y+1)-f(x,y))^2}\) \(=\sqrt{(z_6-z_5)^2+(z_8-z_5)^2}\approx|z_6-z_5|+|z_8-z_5|\) 得到基本梯度算子(保证一正一负即可,有绝对值) x掩膜:\(\left|\begin{matrix}1 & -1\\0 & 0\\\end{matrix}\right|\);y掩膜:\(\left|\begin{matrix}1 & 0\\-1 & 0\\\end{matrix}\right|\) 如果α=1.则是Roberts算子:x淹膜:\(\left|\begin{matrix}-1 & 0\\0 & 1\\\end{matrix}\right|\);y掩膜:\(\left|\begin{matrix}0 & -1\\1 & 0\\\end{matrix}\right|\) 这个算子边缘定位准,对噪声敏感,突出斜线 Sobel梯度算子 \(M(x,y)\approx |(z_7+2z_8+z_9)-(z_1+2z_2+z_3)|+|(z_3+2z_6+z_9)-(z_1+2z_4+z_7)|\) x掩膜:\(\left|\begin{matrix}-1 & -2 & -1\\0 & 0 & 0\\1 & 2 & 1\\\end{matrix}\right|\);y掩膜:\(\left|\begin{matrix}-1 & 0 & 1\\-2 & 0 & 2\\-1 & 0 & 1\\\end{matrix}\right|\) 优点: 混合空间增强 使用多个滤波器,当使用线性滤波器时,在数学上是可以换序的(不能对整型灰度操作)
\[
s=T[r]=\begin{cases}
s_0, r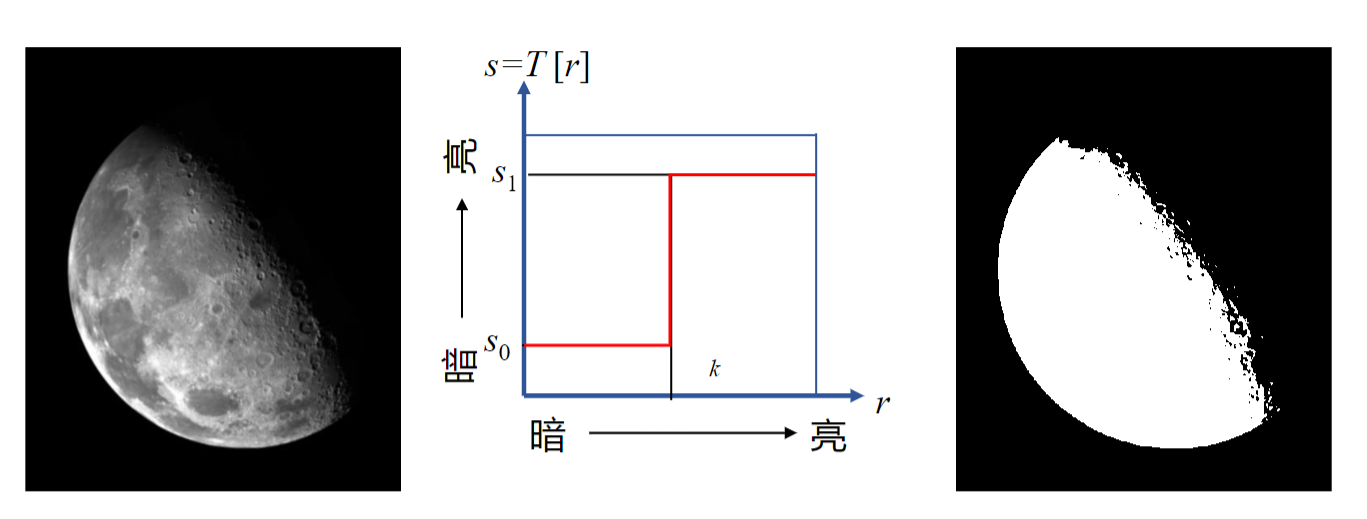
\[
s=T[r]=L-r-1
\]
注意要-1,防止溢出,增强暗区域中的亮细节或亮区域内的暗细节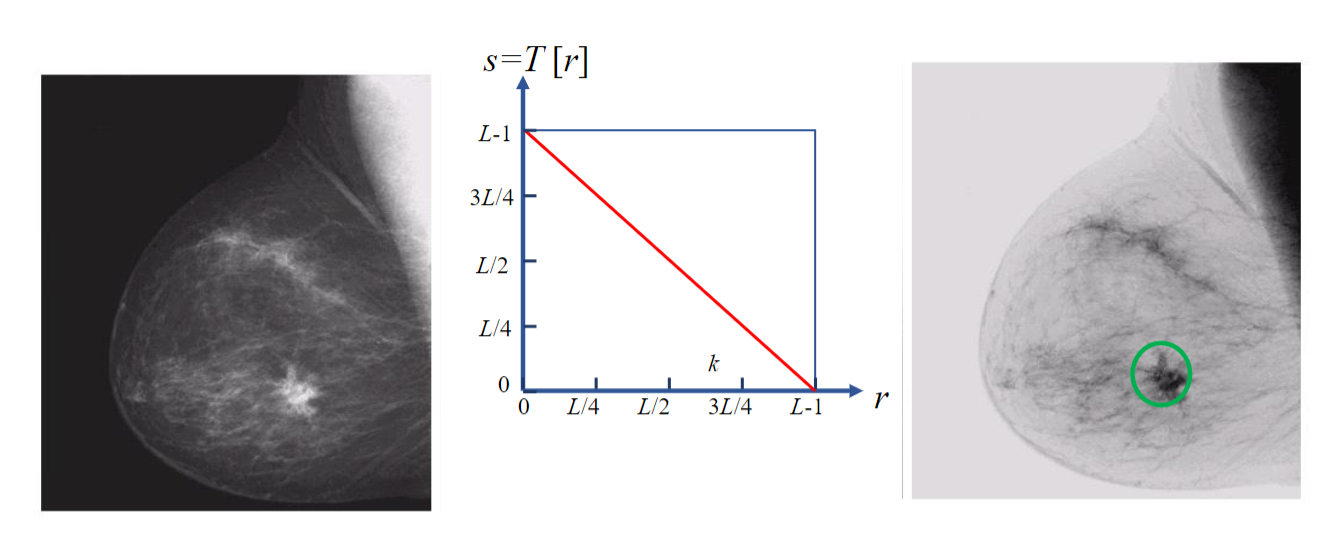
\[
s=T[r]=c\log{(1+r)}
\]
低灰度区:拉伸;高灰度区:压缩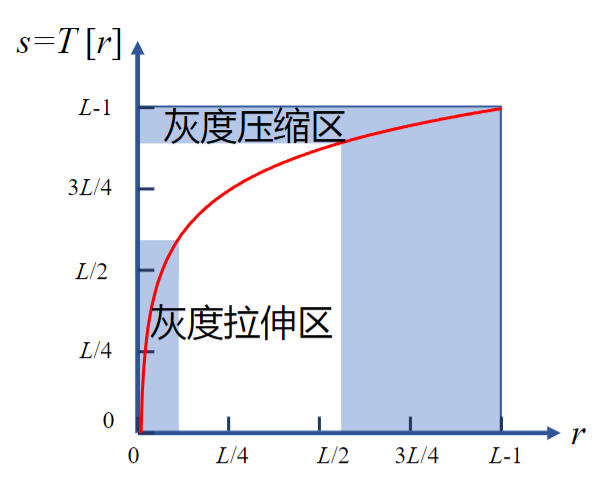
\[
s=T[r]=cr^\gamma
\]
也称伽马变换;γ>1,压缩低灰度区;γ<1,扩展低灰度区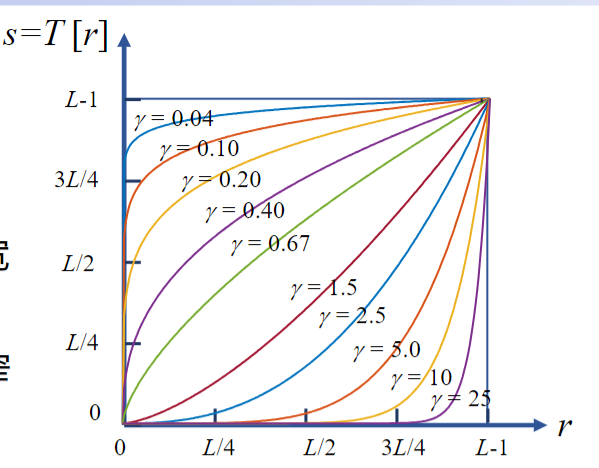
十进制灰度
比特平面8
比特平面7
...
比特平面1
0
0
0
...
0
1
0
0
...
1
...
...
...
...
...
255
1
1
...
1
3.2 直方图处理
3.2.1 直方图均衡化

3.2.2直方图规定化
3.2.3局部直方图均衡化
3.3 空间滤波
3.3.1 基础定义
\[
g(x,y)=\sum\limits_{s=-(m-1)/2}^{(m-1)/2}\,\sum\limits_{t=-(n-1)/2}^{(n-1)/2}w(s,t)f(x+s,y+t)
\]
即
\[
\left|\begin{matrix}
a & b & c\\
d & e & f\\
g & h & i\\
\end{matrix}\right|
*
\left|\begin{matrix}
z & y & x\\
w & v & u\\
t & s & r\\
\end{matrix}\right|
=az+by+cx+dw+ev+fu+gt+hs+ir
\]
\[
g(x,y)=\sum\limits_{s=-(m-1)/2}^{(m-1)/2}\,\sum\limits_{t=-(n-1)/2}^{(n-1)/2}w(s,t)f(x-s,y-t)=\sum\limits_{s=-(m-1)/2}^{(m-1)/2}\,\sum\limits_{t=-(n-1)/2}^{(n-1)/2}w(-s,-t)f(x+s,y+t)
\]
即先将模板中心对称,然后做相关运算
\[
\left|\begin{matrix}
a & b & c\\
d & e & f\\
g & h & i\\
\end{matrix}\right|
*
\left|\begin{matrix}
z & y & x\\
w & v & u\\
t & s & r\\
\end{matrix}\right|
=ar+bs+ct+du+ev+fw+gx+hy+iz
\]3.3.2 边界处理

3.3.3 空间滤波器分类

3.3.4 平滑滤波器

3.3.5 锐化滤波器
\[
\nabla^2f=\frac{\part^2f}{\part x^2}+\frac{\part^2f}{\part y^2}
\]
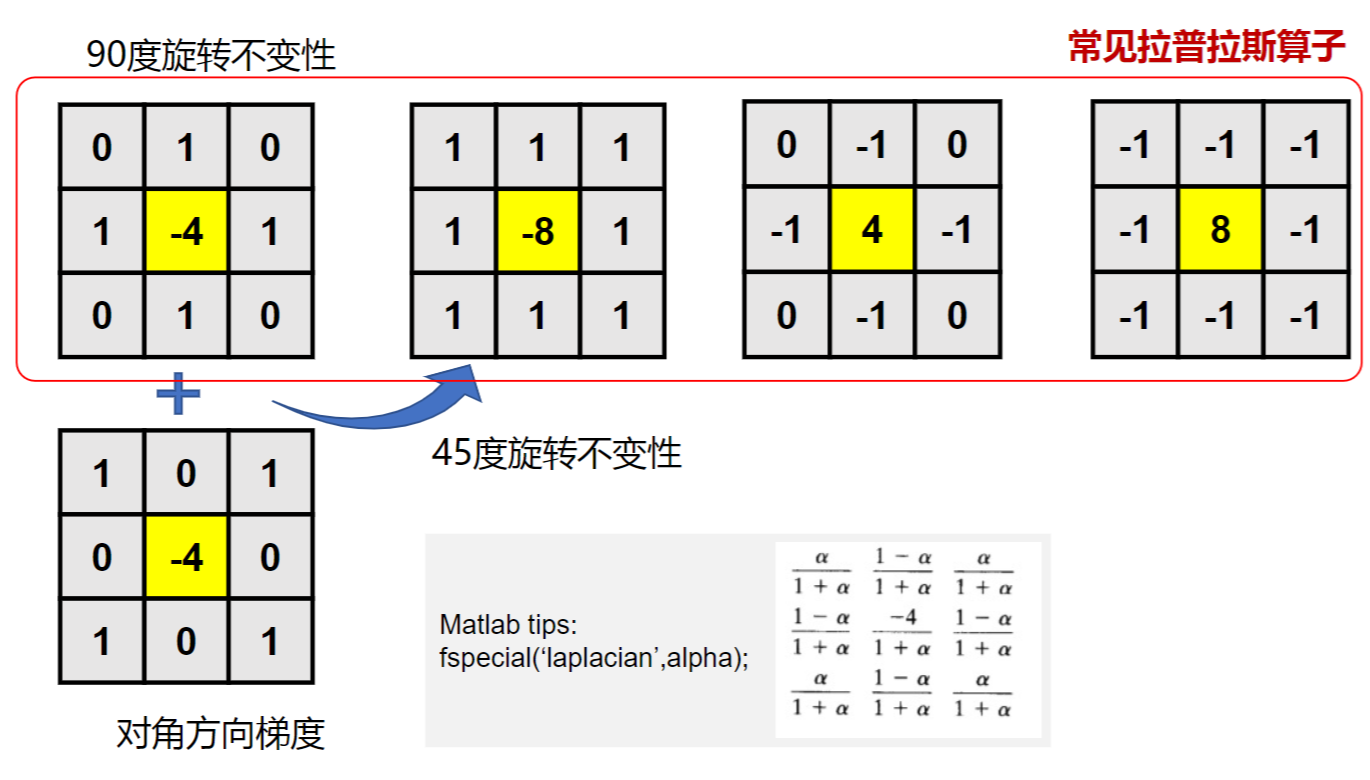
Laplace算子的模板是
\[
\left|\begin{matrix}
0 & 1 & 0\\
1 & -4 & 1\\
0 & 1 & 0\\
\end{matrix}\right|
\]
是最简单的各向同性算子(旋转90°不变),且是线性的
\[
\left|\begin{matrix}
1 & 0 & 1\\
0 & -4 & 0\\
1 & 0 & 1\\
\end{matrix}\right|
\]
\[
\left|\begin{matrix}
0 & -1 & 0\\
-1 & 5 & -1\\
0 & -1 & 0\\
\end{matrix}\right|
\]
这个模板的锐化效果更好
\[
\left|\begin{matrix}
-1 & -1 & -1\\
-1 & 9 & -1\\
-1 & -1 & -1\\
\end{matrix}\right|
\]