4 数据库设计

学习笔记

作者: MingXiao

概念设计

通常采用E-R模型（Entity-Relationship）

E-R模型	例子
实体	学生，课程
属性	学号，课号
联系	学生与课程之间存在“选课”联系

逻辑设计

常见的有关系模型，层次模型等，前者是主流

关系模型就是第二章所讲

物理设计

在内存/硬盘中的表示

4.1 概念设计

可以使用E-R图表示

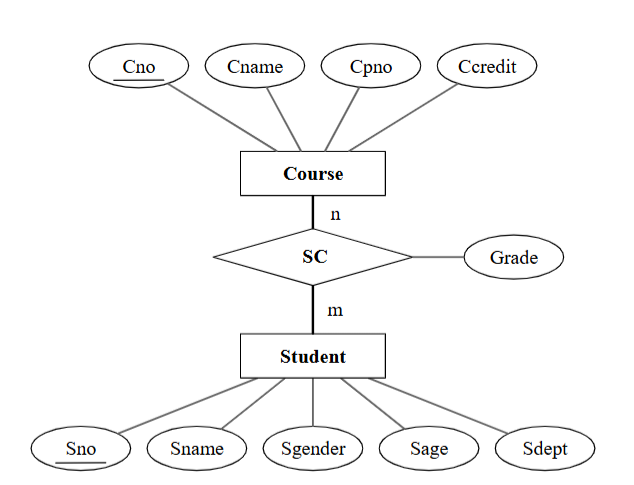
其中

椭圆型：属性，带下划线的是标识符（主键）

方框：实体

菱形框：联系

数字：从对面看，二者的关系数量，图中就是说一个学生对应n门课，一门课对应m个学生，这里的\(m,n\)都是虚指，意思是学生和课程是多对多关系

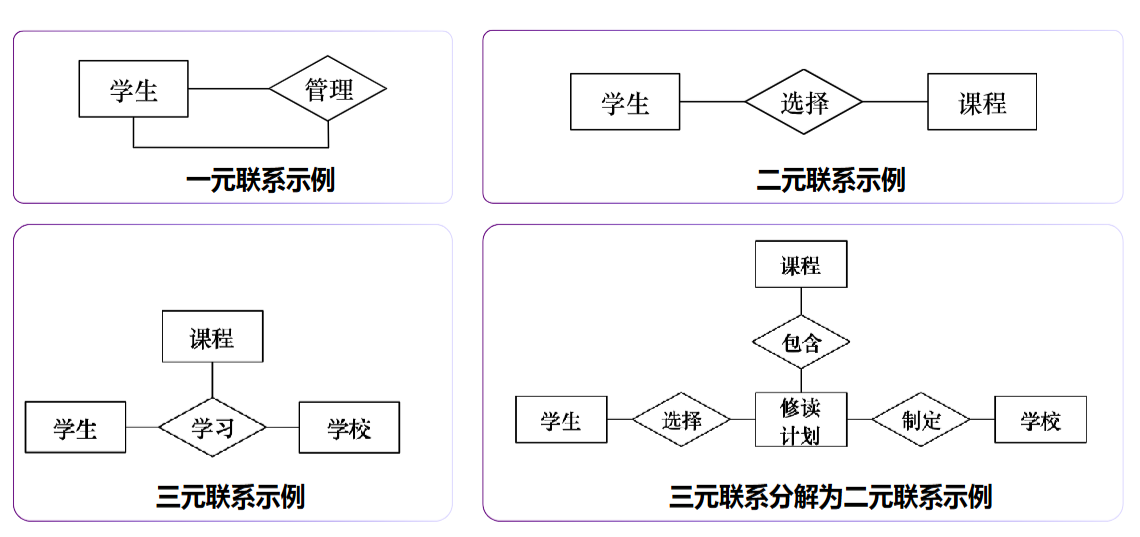
4.1.1 E-R联系类型

统统都可以化为二元联系

4.1.2 实体 OR 属性

简化原则：能当属性的，就不当实体

两条准则：

属性不能包含其他属性
属性不能与其他实体有联系

如下面的例子，如果”职称“与”工资“无关，那么可以向上图定义；但是如果有关，那么就得用下面的模式

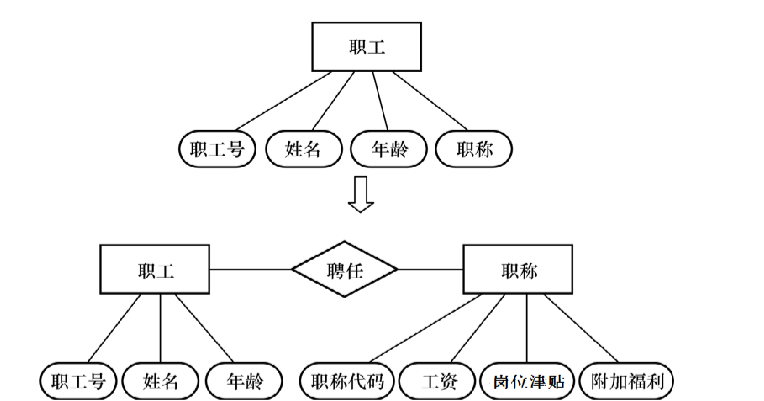
联系属性还是实体属性

联系的属性一般存在于多对多联系，但也不一定

4.1.3 约束

包括属性约束和联系约束，前者见第二章

联系约束

包括基数和参与度

基数：实体参与联系的最大次数，也就是x对x联系中的x

参与度：实体参与的联系的最小次数

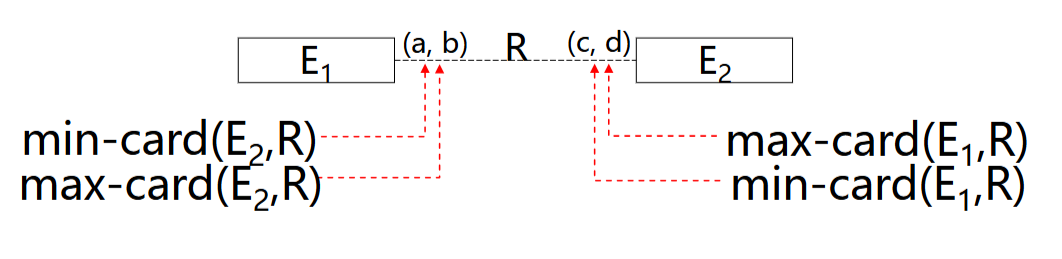
意思是\(E_1\)与\((c,d)\)个\(E_2\)的实体发生联系

4.2 逻辑设计

4.2.1 实体集转换

实体集：关系模式（table）

属性：属性

标识符：键

4.2.2 联系转换

一元/三元联系，都可以用二元联系表示，下面仅讨论二元联系

一对一联系

有两种转换方式

在任意一个关系模式的属性中加入另一个关系模式的键，和联系的属性
添加一个关系模式，包含联系的属性和各个实体集的标识符

一对多联系

有两种转换方式

在n端实体中加入1端实体的标识符和联系的属性
添加一个关系模式，属性是各个实体集的标识符和联系的属性，主键是n端的标识符

多对多联系

添加一个新的关系，属性是各个实体集的标识符和联系的属性，键是两个实体集的标识符的组合

4.3 数据库规范化

4.3.1 函数依赖

一个关系中属性或属性组的依赖和制约关系（约束），定义如下：

给定的关系\(R(U)\)，其中\(X,Y \subseteq U,\,\,\, \forall t,l\in R\)

若\(t[X]=l[X]\Rightarrow t[Y]=l[Y]\)，称\(Y\)函数依赖于\(X\)，或\(X\)函数决定\(Y\)，记为
\[ X\rightarrow Y \]
若不依赖，记为
\[ X\nrightarrow Y \]
若\(X,Y\)相互函数依赖，记为
\[ X \leftrightarrow Y \]
一个函数依赖要成立，需要使\(X,Y\)的任意可能值都满足这个依赖，即使这些值不在表中存在

用函数依赖定义键

一个/多个属性的集合\(K\)满足

其他属于函数依赖于\(K\)
其他属性都不函数依赖于\(K\)的任意真子集

那么\(K\)就是这个关系的键

\(K\)是\(R(U)\)的超键，当且仅当\(K \rightarrow U\)

非/平凡函数依赖

非平凡函数依赖
\[ X\rightarrow Y\and Y\nsubseteq X \]
则称非平凡

反之是子集则为平凡，很好理解一个属性组一定决定自身

所有关系都满足平凡函数依赖，一般指的都是非平凡依赖

完全/部分函数依赖

完全函数依赖
\[ X \rightarrow Y \and X^{'}\nrightarrow Y \Rightarrow X\stackrel{f}{\rightarrow}Y \]
其中\(X^{'}\)是\(X\)的任意真子集，f为fully

否则称部分函数依赖，记为\(X \stackrel{p}{\rightarrow} Y\)

传递函数依赖
\[ X \rightarrow Y\and Y\nrightarrow X\and Y\rightarrow Z \]
则称\(Z\)对\(X\)有传递函数依赖

多值依赖

对于\(R(U)\)，设\(X,Y\subseteq U \,\,\,, Z = U-X-Y\)，当存在\((x,y_1,z_1),(x,y_2,z_2)\)时，也存在\((x,y_1,z_2),(x,y_2,z_1)\)

那么称\(Y\)在\(R\)上多值依赖于\(X\)，记为
\[ X\rightarrow\rightarrow Y \]
也就是对于任意的\(a[X]=b[X] \in R(U[X])\)，交换\(a,b\)的\(Y\)的值，交换后的元组也存在于\(R(U)\)中（不一定在表中），则称\(Y\)多值依赖于\(X\)

直观上说，就是\(X\)决定了\(Y\)的取值范围，\(Y\)的取值与\(Z\)无关

如果\(Z = \phi\)，那么这是平凡多值依赖，反之是非平凡

函数依赖是多值依赖的一个特例，此时取值范围唯一

连接依赖

一个关系分为若干子关系，这些子关系通过连接操作后得到原始关系，则连接依赖成立

多值依赖就是可以分解为两个子关系的连接依赖

4.3.2 关系模式的范式

一个第一辑的范式，通过模式分级可以转换为若干个高一级的范式，这个过程叫规范化

通常分解到第三范式就行

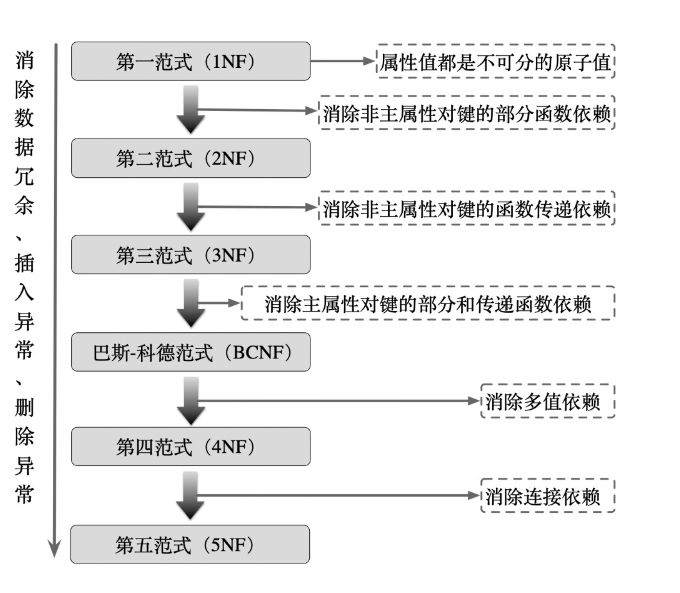
第一范式

指\(R\)中每一个属性都不可再分

第二范式

满足第一范式，且每一个非主属性都完全函数依赖于任一个候选键

主属性：包含在候选键中的所有属性，即使不是主键

如果一个关系只有一个候选键，那么一定满足第二范式

第三范式

满足第一范式，不存在非主属性对候选键的传递函数依赖

巴斯-科德范式

满足第三范式，任何属性都非平凡地完全函数依赖于\(R\)的候选键

即：\(X\rightarrow Y \and Y\nsubseteq X\Rightarrow X\)是超键

如果一个关系满足BCNF，那么在函数依赖的范围内，它已经实现了关系模式的彻底分解，消除了插入和删除异常

3NF和BCNF的联系

满足BCNF，一定满足3NF
满足3NF，且只有一个候选键，则满足BCNF

第四范式

满足BCNF，消除了多值依赖

4.4 数据依赖的公理系统

4.4.1 Armstrong公理系统

逻辑蕴含

对于满足函数依赖\(F\)的关系\(R\)，函数依赖\(X\rightarrow Y\)成立，则称\(F\)逻辑蕴含\(X\rightarrow Y\)

将\(F\)蕴含的所有函数依赖的集合称为\(F\)的闭包，寻找这个集合的推理规则就是Armstrong公理系统

公理定义

\(R,U=\{A_1,A_2,\ldots ,A_n\}\)，存在以下规则

自反律：\(Y\subseteq X\subseteq U\)，则\(X\rightarrow Y\)为\(F\)所蕴含（平凡函数依赖）
增广律：\(X\rightarrow Y\)为\(F\)所蕴含，且\(Z\subseteq U\)，则\(XZ\rightarrow YZ\)为\(F\)所蕴含，其中\(AB\)表示集合\(A\cup B\)
传递律：\(X\rightarrow Y,Y\rightarrow Z\)为\(F\)所蕴含，则\(X\rightarrow Z\)为\(F\)所蕴含

根据公理可以推出以下推理规则

合并规则：\(X\rightarrow Y,X\rightarrow Z\)，则\(X \rightarrow YZ\)
分解规则：\(X\rightarrow Y, Z\subseteq Y\)，则\(X\rightarrow Z\)
伪传递规则：\(X\rightarrow Y, WY\rightarrow Z\)，则\(XW\rightarrow Z\)

还有一条引理：\(X\rightarrow \Pi A_i\)成立的充要条件是\(X\rightarrow A_i\)成立

4.4.2 函数依赖的闭包

将\(F\)蕴含的所有函数依赖的集合称为\(F\)的闭包，记作\(F^+\)

属性集的闭包：\(X_{F}^+=\{A|(X\rightarrow A)\in F^+\}\)，很显然\(F^+ = \bigcup X_i\rightarrow Y_i\)

如何计算

输入：\(X,F\)

输出：\(X^+_F\)

算法：

一个序列\(X^{(i)}\)，令\(X^{(0)}=X\)
求\(B\)，其中\(B=\{A|(\exist V)(\exist W)(V\rightarrow W\and V\subseteq X^{(i)})\and A\in W\}\)
\(X^{(i+1)} = X^{(i)}\cup B\)
当\(X^{(i)}\)不再变化时，迭代结束

步骤二相当于将\(X^{(i)}\)的子集的函数依赖的右边加入\(B\)中

例：如图

属性集闭包的作用

判断函数依赖是否成立：\(X\rightarrow Y \in F^+\Leftrightarrow Y\subseteq X^+_F\)
判断是否是键：\(X^+_F = U\)，则\(X\)是超键；若还有\(X\)的任意子集不满足前式，则\(X\)是候选键

4.4.3 函数依赖的等价和最小函数依赖集

函数依赖的等价：\(F^+ = G^+\)，则\(F\)与\(G\)等价

但是求闭包开销很大，这里给出等价的充要条件：\(F\subseteq G^+ \and G\subseteq F^+\)

前者很容易证明后者，这里给出充分性证明：

\(\forall X\rightarrow Y\in F^+\)，有\(Y\subseteq X^+_F\subseteq X^+_{G^+}\)，故\(X\rightarrow Y\in (G^+)^+=G^+\)，故\(F^+\subseteq G^+\)；同理可以证明另一边

而判断\(F\subseteq G^+\)是否成立就是判断\(\forall X\rightarrow Y \in F^+\)，是否有\(Y\subseteq X^+_G\)

最小函数依赖集（最小覆盖）

当函数依赖集\(F\)满足以下条件时，是最小覆盖

\(F\)中任一函数依赖的右边只有一个属性
\(F\)中不存在多余的函数依赖（就是不能有能被余下的函数依赖蕴含的依赖）
\(F\)中的任一函数依赖的左边没有多余的属性

每一个函数依赖集都等价于一个最小覆盖\(F_m\)，且\(F_m\)不唯一

4.5 基于关系模式的分解

4.5.1 关系模式分解

对于关系模式\(R\)，其分解指的是\(\rho =\{R_1, R_2,\ldots ,R_n\}\)

并且这个分解需要满足

关系不丢失：\(U = \bigcup U_i\)
模式不冗余：不存在\(U_i \subseteq U_j\)
依赖不丢失：\(F_i\)是\(F\)在\(U_i\)上的投影，\(F_i=\{X\rightarrow Y|X\rightarrow Y \in F^+\and XY\subseteq U_i\}\)

分解有很多种，但需要满足分解前后的等价性

数据等价：分解的无损链接性，指分解后的关系可以通过自然连接恢复为原关系
语义等价：分解要保持函数依赖

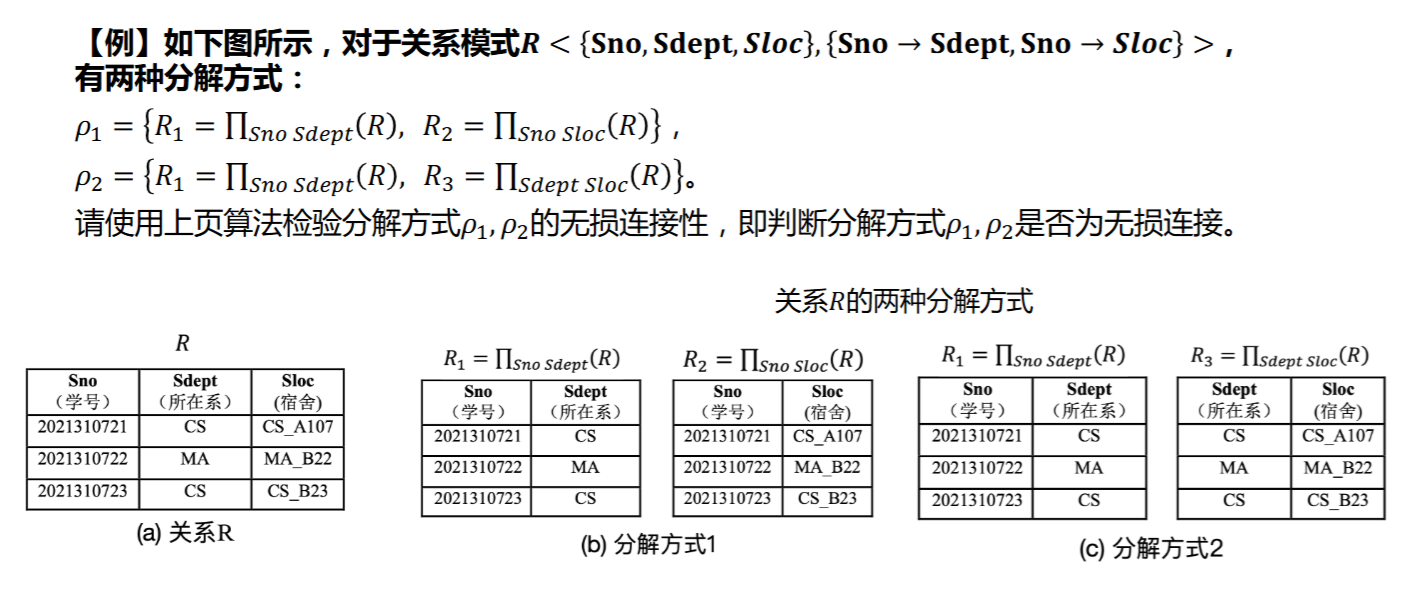
4.5.2 检验无损分解的算法

输入：\(R<\{A_1,A_2,\ldots,A_n\},F>,\rho=\{R_1,R_2.\ldots ,R_m\}\)

输出：\(\rho\)是否为无损分解

算法：

构造一个m行n列表，每一行对应一个分解的关系模式，每一列对应一个属性
\(A_j\in R_i\)，则在第i行，第j列标记上\(a_j\)，否则为\(b_{ij}\)
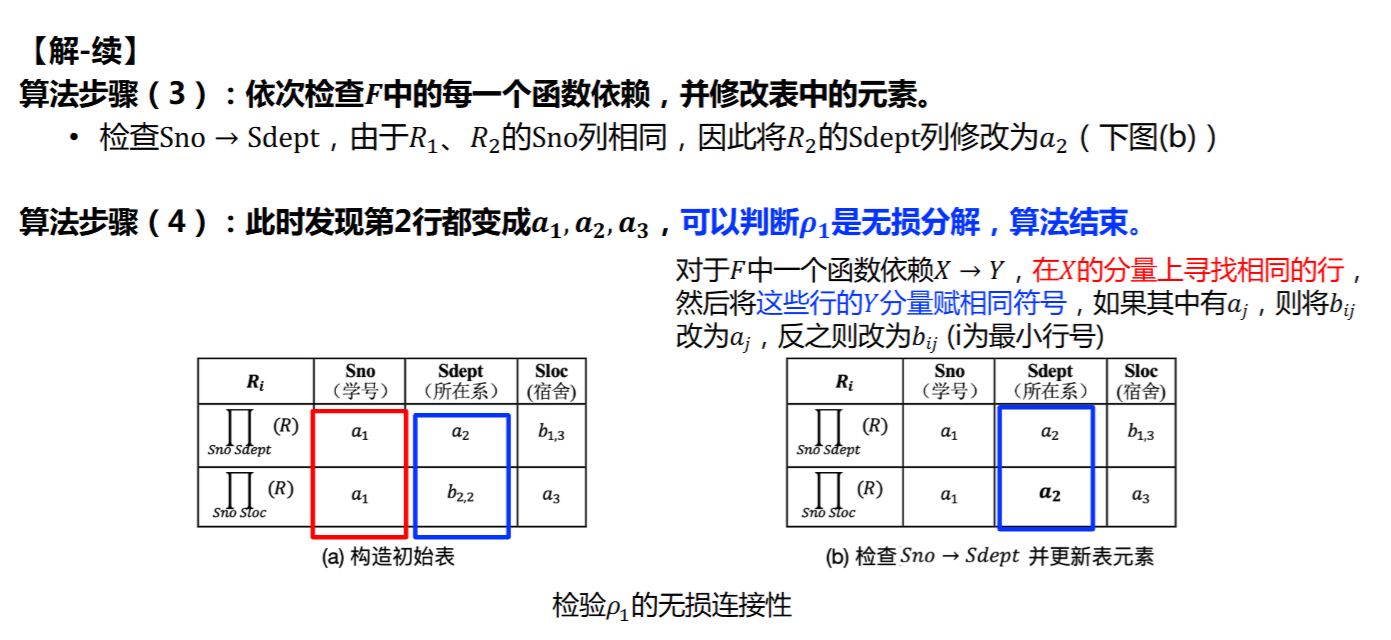
依次检查\(F\)中的每一个函数依赖，若\(X\rightarrow Y\in F\)，在\(X\)的分量上寻找标记相同的行，将这些行的\(Y\)的标记改为相同值，若存在\(a_j\)则标记为\(a_j\)，否则标记为\(i\)最小的\(b_{ij}\)
如果存在一行为\(a_1,a_2,\ldots ,a_n\)，那么\(\rho\)是无损分解，否则不是
做完一轮\(F\)还得再做几轮，直到没有标号的改变为止

例：如图