2 物理量传感器

学习笔记

作者: MingXiao

2.1 电阻式传感器

2.1.1 应用

一个典型的应用是测量血压

正常的血压范围：90/60 mmHg ~ 140/90 mmHg

当外界施加的压力与血压相等时，产生共振，发出的信号幅度最大

一个典型的血压仪框图如图

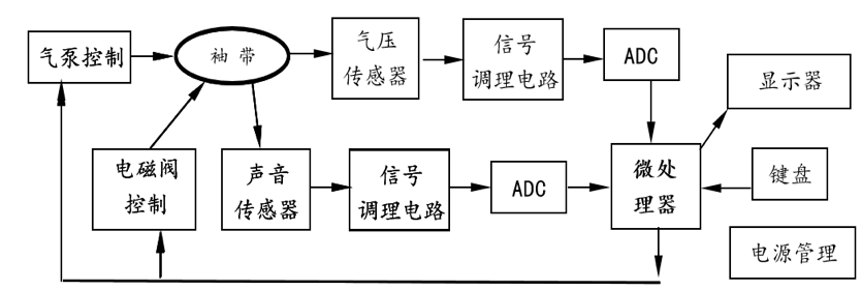
其中气压传感器如下

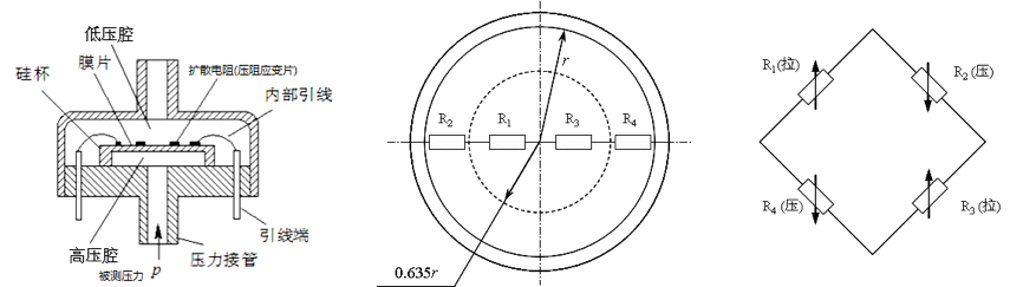
如何设计

先查标准，血压仪的测量范围要在4000 -- -400 mmHg，保护用

2.1.2 电阻应变式传感器

2.1.2.1 电阻应变效应

电阻的计算公式为\(R=\rho\frac{l}{s}\)，很显然对于\(\rho,l\)，R的响应是线性的，而s是非线性的

对上式取对数并求导得到
\[ \frac{dR}{R}=\frac{d\rho}{\rho}+\frac{dl}{l}-\frac{ds}{s} \]
其中\(\frac{dl}{l}=\varepsilon\)为正应变，由于正应变与切应变满足\(\tau=-\mu\varepsilon\)，即\(\frac{dr}{r}=-\mu\frac{dl}{l}\)

对\(s=\pi r^2\)取对数求导得到\(\frac{ds}{s}=2\frac{dr}{r}=-2\mu\frac{dl}{l}\)

\(\frac{d\rho}{\rho}=\pi_l\sigma=\pi_lE\varepsilon\)，其中\(\pi_l\)为材料沿某晶向的压阻系数，金属约为0，半导体不为0；\(\sigma\)是应力，\(E\)是杨氏模量

将上面格式带入原式，得到
\[ \frac{dR}{R}=(\pi_lE+1+2\mu)\frac{\sigma}{E}=(\pi_lE+1+2\mu)\varepsilon \]
称为电阻应变效应

将电阻丝的灵敏度定义为单位应变引起的电阻相对变化，计算灵敏度

金属：测量范围广，线性度高

半导体：灵敏度高，温漂大

2.1.2.2 电阻应变片

通常长这样

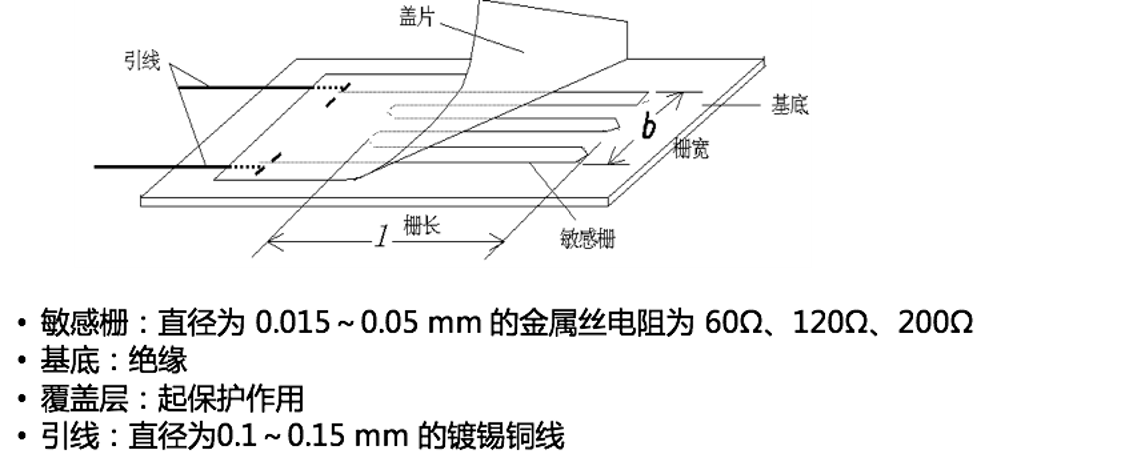
中间绕很多层可以增加正应变，增大电阻变化

优缺点

优点

测量范围广
结构简单
便宜，多样

缺点

易产生温漂和零漂：电阻发热
对于大应变有较大的非线性，但是可以补偿
输出易受环境影响
高功耗

电阻式传感器在自动测试和控制技术中广泛应用

温漂补偿

单丝自补偿应变片
双丝组合式自补偿应变片
电路补偿（最常用）

其中2的方法具体是

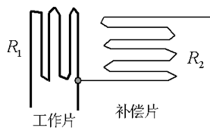
补偿片不在拉伸方向上，产生的应变可以不计，但是二者的温漂是一致的，差分得到结果

2.1.3 电桥

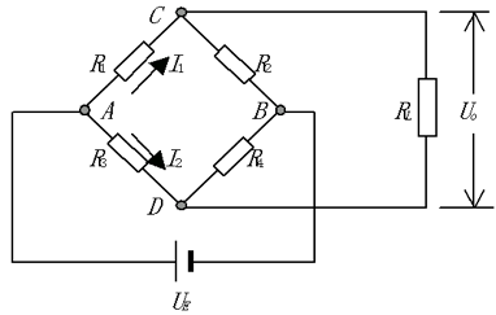
电桥平衡条件：\(R_1R_4 = R_2R_3\)

负载\(R_L\)很大，可以视为断路，此时的\(U_0\)为
\[ U_0 = U_E \frac{R_1R_4-R_2R_3}{(R_1+R_4)(R_2+R_3)} \]
定义平衡时的桥臂比\(n = \frac{R_2}{R_1}=\frac{R_4}{R_3}\)

若\(R_1\)是电阻传感器，其他是定值电阻，定义\(\delta_R = \frac{\Delta R}{R_1}\)，那么有
\[ U_0 = U_E \frac{n\delta_R}{(1+n)(1+\delta_R+n)} \]
由上文，\(\delta_R = K_s \varepsilon\)，这个值往往很小，有\(\delta_R < < 1\)，那么有
\[ U_0^{'} = U_E \frac{n}{(1+n)^2}\cdot \delta_R \]
定义灵敏度\(K_U = \frac{U_0}{\delta_R}=\frac{n}{(1+n)^2}U_E\)，显然\(n=1\)时取最大值，\(U_E\)不能过大（温漂压不住）

这样近似的非线性误差为
\[ \gamma = \left|\frac{ U_0 -U_0^{'}}{U_0^{'}} \right| = \frac{\delta_R}{1+\delta_R+n} \]
是比较小的

上面是单臂电桥，还有其他的

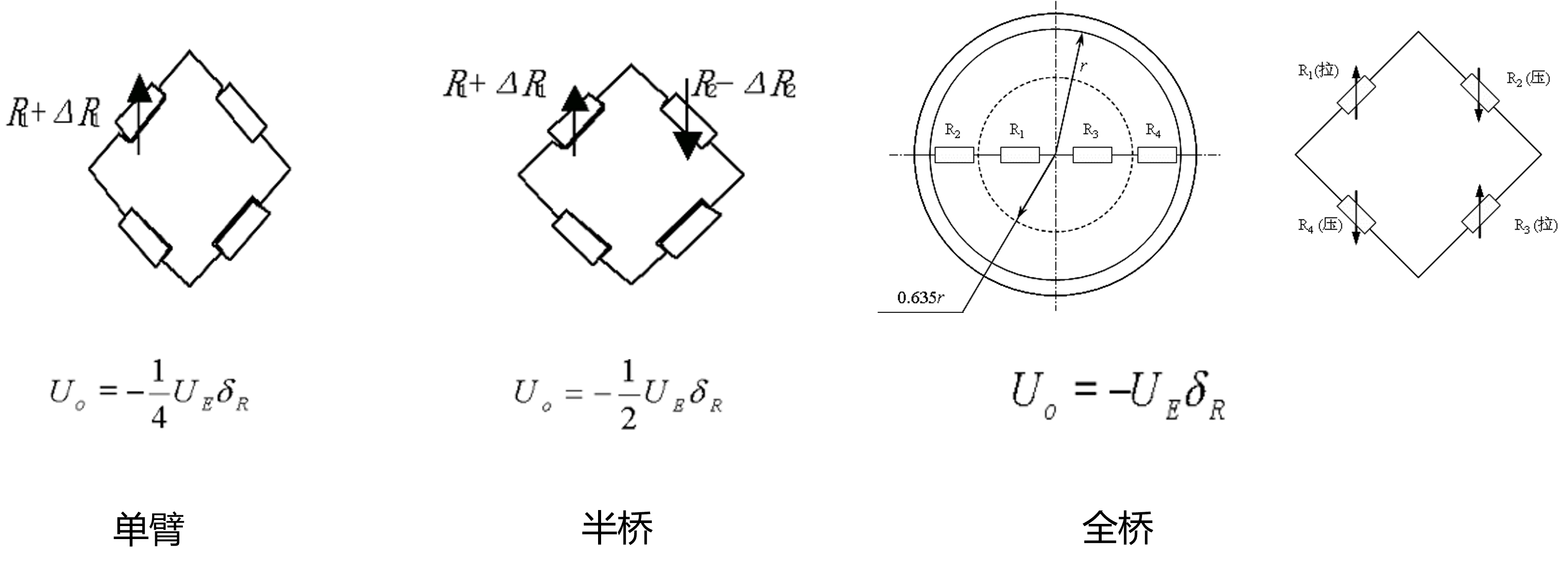
都是\(n=1\)

半桥
\[ U_0 = U_E\left(\frac{R+\Delta R}{2R}-\frac{R}{2R}\right)=U_E\frac{\Delta R}{2R} \]
无非线性误差，灵敏度是单臂的2倍，还有温度补偿作用

全桥
\[ U_0 = U_E\left(\frac{R+\Delta R}{2R}-\frac{R-\Delta R}{2R}\right)=U_E\frac{\Delta R}{R} \]
无非线性误差，灵敏度是单臂的4倍，有温度补偿作用

\(U_o\)一般都比较小，需要直流放大器，但是直流的电路容易零漂，因此就有了交流电桥

2.2 电容式传感器

2.2.1 应用

触摸屏，麦克风

电容式心音传感器

助听器，一般使用驻极体作为电容材料，没有电压也有电荷存在，减小能耗

2.2.2 电容传感器

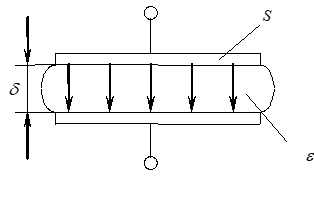
不考虑边缘效应，\(C=\frac{Q}{U}\)，用高斯定理可得，平行板电容器\(C=\frac{\varepsilon S}{d}\)

当极板受压时，极板间距\(d\)发生变化，导致电容C的变化，\(C^{'} = \frac{\varepsilon S}{d-\Delta d}\)，\(\Delta C =C^{'}-C_0=C_0\frac{\Delta d/d}{1-\Delta d/d}\)

得到
\[ \Delta C /C_0=\frac{\Delta d/d}{1-\Delta d/d}=\frac{\Delta d}{d}\sum_{n=0}^{+\infty} \left(\frac{\Delta d}{d}\right)^n=\frac{\Delta d}{d}\cdot\left(1+\frac{\Delta d}{d}+\left(\frac{\Delta d}{d}\right)^2+\ldots\right) \]
可以发现C与d是非线性的关系

当\(\Delta d<< d_0\)时，可以近似舍去2次及以上项，得到
\[ \frac{\Delta C}{C}=\frac{\Delta d}{d} \]
灵敏度\(K=\frac{\Delta C /C_0}{\Delta d }=\frac{1}{d}\mathsf{mm^{-1}}\)或\(K=\frac{\Delta C /C_0}{\Delta d /d}=1\)，后者无量纲

由此近似的模型在\((0,\Delta d)\)内的非线性误差（与保留到二次项对比）为\(\delta = (\frac{\Delta d}{d})^2/\frac{\Delta d}{d}=\frac{\Delta d}{d}\)，发现d相对Δd越大，线性度越好

为什么不用电阻式的分析方式？

那样可以很容易看出灵敏度K，但是看不出非线性误差δ
定义的变化量也不同，电阻定义应变\(\varepsilon=\frac{\Delta l }{l}\)，而电容使用的是\(\Delta d\)
那样分析也存在误差

2.2.3 差动变极距型电容式传感器

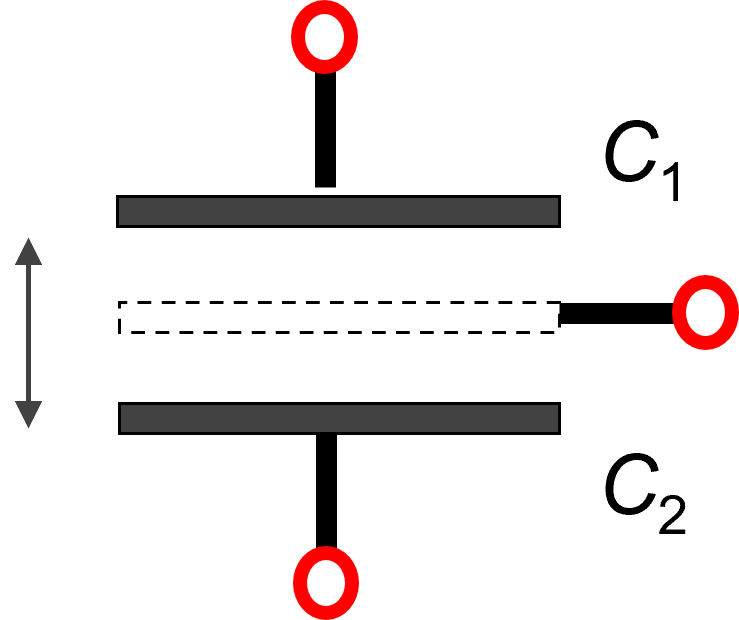
\[ \Delta C_1 /C_0=\frac{\Delta d}{d}\cdot\left(1+\frac{\Delta d}{d}+\left(\frac{\Delta d}{d}\right)^2+\ldots\right)\\ \Delta C_2 /C_0=-\frac{\Delta d}{d}\cdot\left(1-\frac{\Delta d}{d}+\left(\frac{\Delta d}{d}\right)^2+\ldots\right) \]

用差分电路检测两个电容的差值\(\Delta C_1/C_0-\Delta C_2/C_0\)，得到
\[ \Delta C_1/C_0-\Delta C_2/C_0=2\frac{\Delta d}{d}\cdot\left(1+\left(\frac{\Delta d}{d}\right)^2+\ldots\right) \]
灵敏度\(K=\frac{2}{d}\)，非线性误差\(\delta = \left( \frac{\Delta d}{d}\right)^2\)

这是假设向\(C_1\)移动

2.2.4 差动传感器材料和结构选择

\(d_0\)较小，灵敏度高；过小则容易引起击穿

极板间使用高介电常数材料（云母），此时\(C=\frac{S}{\frac{d_g}{\varepsilon_g \varepsilon_0}+\frac{d_0}{\varepsilon_0}}\)，由于\(\frac{d_g}{\varepsilon_g \varepsilon_0}\)是常数，这可以让非线性误差减小

2.2.5 变面积和变介质式传感器

变面积式

可以横向位移，\(C=\frac{\varepsilon b x}{d}\)，b为宽度，x可变
\[ \Delta C = \frac{\varepsilon b}{d}\Delta x \]
是线性的，\(K=\frac{\Delta C}{\Delta x}=\frac{\varepsilon b}{d}=\mathsf{const}\)

变介质式

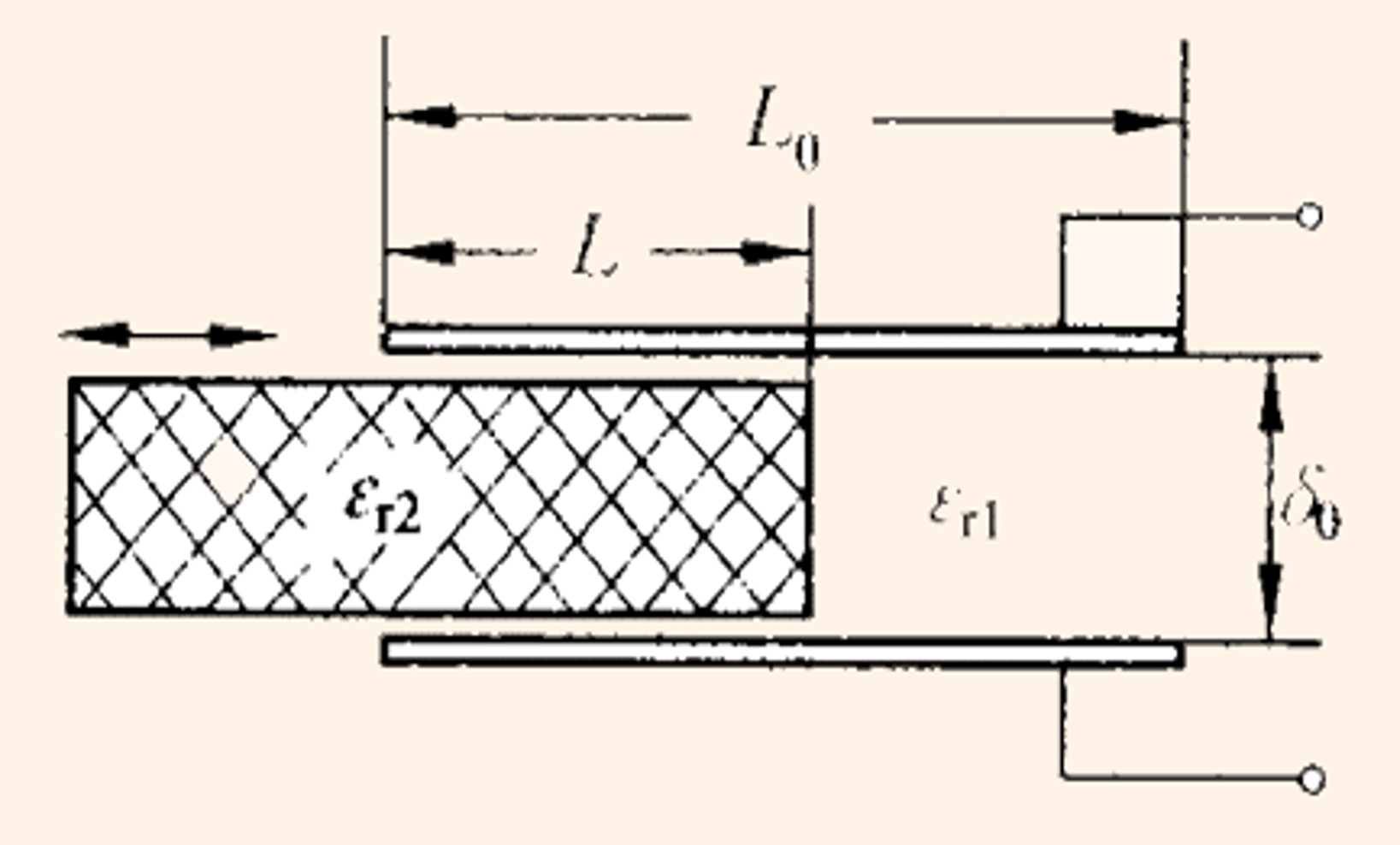
视为两个电容并联，\(C=\frac{\varepsilon_0}{d}(\varepsilon_{r1}(l_0-l)b+\varepsilon_{r2}lb)\)

若右边是空气且\(l\)一开始为0，则
\[ \frac{\Delta C}{C_0}=\frac{(\varepsilon_{r2}-1)\Delta l}{l_0} \]
是线性的

2.2.6 电容式传感器优缺点

优点

温漂小（发热小）
结构简单
动态响应好
非接触式
能耗低

缺点

阻抗大，带载能力弱
寄生电容影响
非线性，测量范围小
成本高

2.3 光电式传感器

2.3.1 应用

典型应用是血氧仪

原理如下：

血液是胶体，当光通过均匀无散射的溶液时，溶液的透光系数如下
\[ T = \frac{I}{I_0}=10^{-acl}\\ A = -\lg\frac{I}{I_0} =-\lg{T}=acl \]
其中a是液体吸光系数，c是溶液摩尔浓度，l是光程

血液中存在两种红细胞，一种富氧，一种乏氧，富氧细胞占总细胞的百分数即为血氧值，记为\(\mathsf{SaO_2}\)

血液的总吸光系数为\(a=a_o\mathsf{SaO_2}+a_H(1-\mathsf{SaO_2})\)，其中\(a_o\)是富氧的系数，\(a_H\)是乏氧的系数

使用两个波长的光对样品进行检测，得到
\[ \lambda_1 : A_1 = \left[(a_o-a_H)\mathsf{SaO_2}+a_H\right]cl\\ \lambda_2 : A_2 = \left[(b_o-b_H)\mathsf{SaO_2}+b_H\right]cl\\ Q = \frac{A_1}{A_2} = \frac{\left[(a_o-a_H)\mathsf{SaO_2}+a_H\right]}{\left[(b_o-b_H)\mathsf{SaO_2}+b_H\right]} \]
得到\(\mathsf{SaO_2}\)的值为
\[ \mathsf{SaO_2}=\frac{a_H-Qb_H}{(b_o-b_H)Q-(a_o-a_H)} \]
要使传感器是线性的，就让\(b_o=b_H=b\)，选择合适的波长的光可以做到，得到最终表达式
\[ \mathsf{SaO_2} = \frac{b}{a_o-a_H}Q-\frac{a_H}{a_o-a_H} \]

2.3.2 内光电效应

当半导体材料受光照时，对光子的吸收会在材料内部激发电子-空穴对，使物体的电导率变化或产生光电动势，分别对应光电导效应和光生伏特效应

2.3.2.1 光电导效应

光电导体受光线作用，其电导率发生变化

本质是价带中的电子受到能量大于或等于禁带宽度的光子轰击，使其跃入导带，导带中的电子和价带中的空穴浓度增加，电导率变大

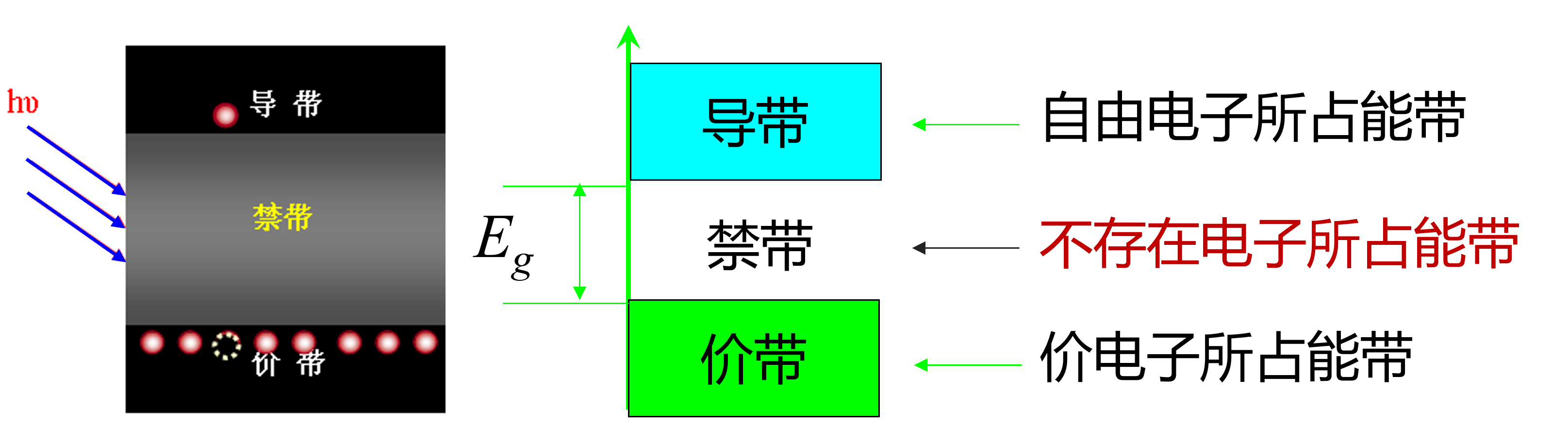
应用：光敏电阻，光导管

2.3.2.2 光生伏特效应

光线作用下，半导体或电介质产生一定方向的电动势

在PN结及附近吸收足够能量的光子后，产生载流子，在内电场（耗尽层，N指向P）作用下，电子由P区涌入N区，空穴相反，使得P区带正电，N区带负电，并在外回路产生电流

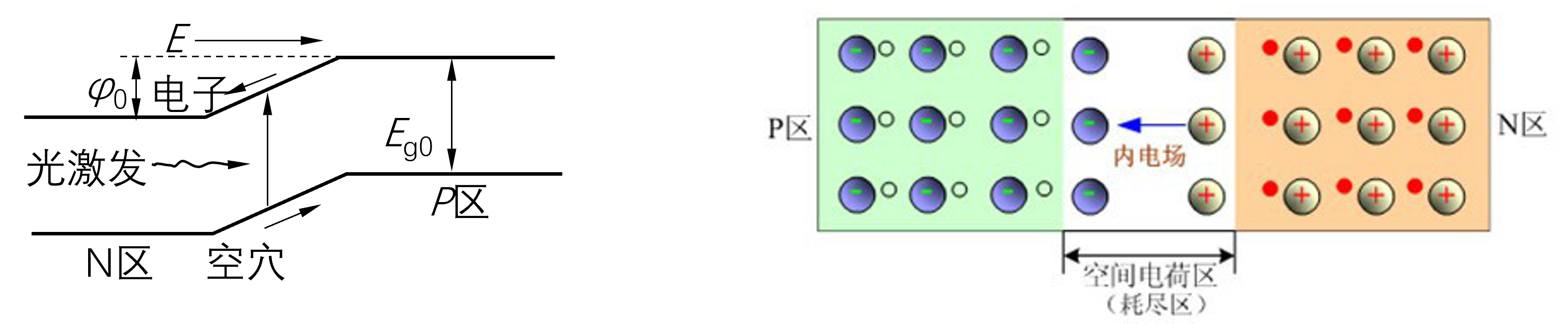
应用：光电池，光敏二极管

2.3.3 外光电效应

光子能量足够大，使物质表面逸出电子
\[ h\nu = \frac{1}{2}mv_m^2+\phi \]
不赘述

应用：光电管，光电倍增管

2.3.4 光电式传感器的特性参数

灵敏度

定义为输出信号\(S\)的变化量与入射光功率变化量\(P_s\)之比
\[ K = \frac{\Delta S}{\Delta P_s}=\frac{\Delta S}{\Delta H A_d} \]
其中H是辐照度变化，Ad是受光面积

光谱特性

传感器的灵敏度和入射光波长的关系

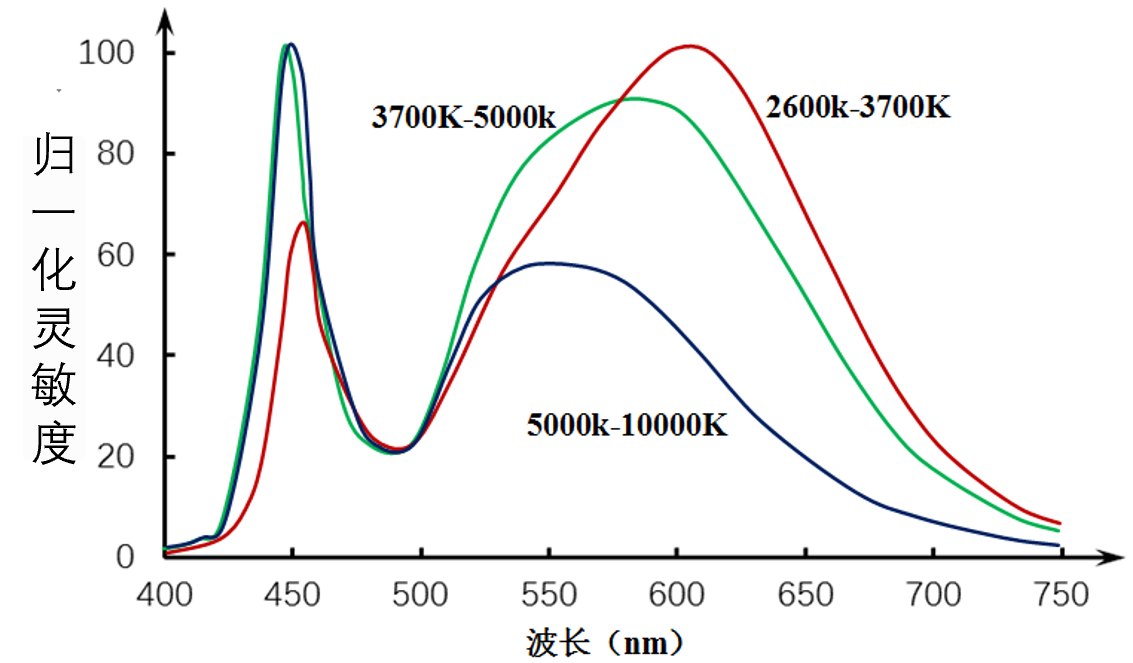
线性度

输出信号与输入光功率成线性比例的程度和范围

响应时间

对入射光变化的响应快慢，是叫时间常数

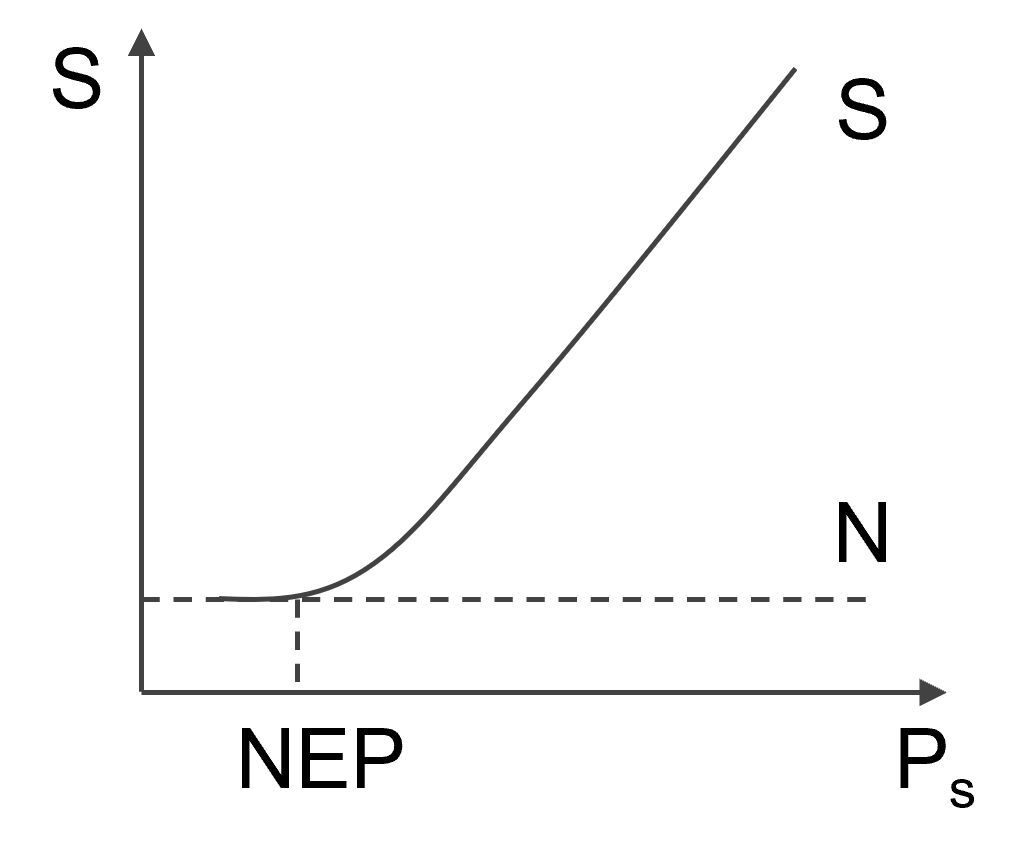
等效噪声功率

产生强度正好等于传感器的噪声输出值的辐射功率，用NEP表示，是表征传感器的品质优劣的重要参数
\[ NEP = P_s\frac{S}{N} \]
其中S/N是信号/噪声的有效值（方均根），S/N是信噪比，NEP越小，性能越好

还有其他传感器都有的特性

2.3.5 光电敏感器件

2.3.5.1 光敏电阻

使用半导体材料制成的电阻，光照作用于半导体时，载流子密度发生变化，电导率变化（光电导效应）

光敏电阻没有极性，可以加交流电

结构示意图如下

参数

暗电阻：不受光时的阻值，很大（MΩ），此时的电流是暗电流

亮电阻：受光照射的阻值，比较小（kΩ），亮电流

光电流：亮电流 - 暗电流

希望暗电阻越大、亮电阻越小越好

特性

伏安特性：在一定照度下的伏安关系。在一定电压范围，I-U为直线；入射光不同，I-U斜率不同

光谱特性：光敏电阻的相对灵敏度与入射波长的关系

温度特性：影响光谱响应、灵敏度和暗电阻等

优点：灵敏度高；光谱响应范围宽

缺点：强光下线性度差；光电弛豫时间长；频率响应低；发热

2.3.5.2 光电管

光线照射到金属感光材料时，有电子逸出（外光电效应），在外加电场作用下移动到阳极，在光电管内部产生电子流，在外电路产生电流

光电子数目（电流大小）与光照强度有关

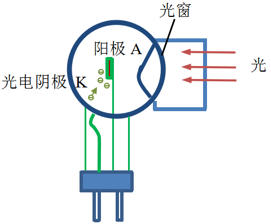
中间是阳极，四周是金属感光材料的阴极

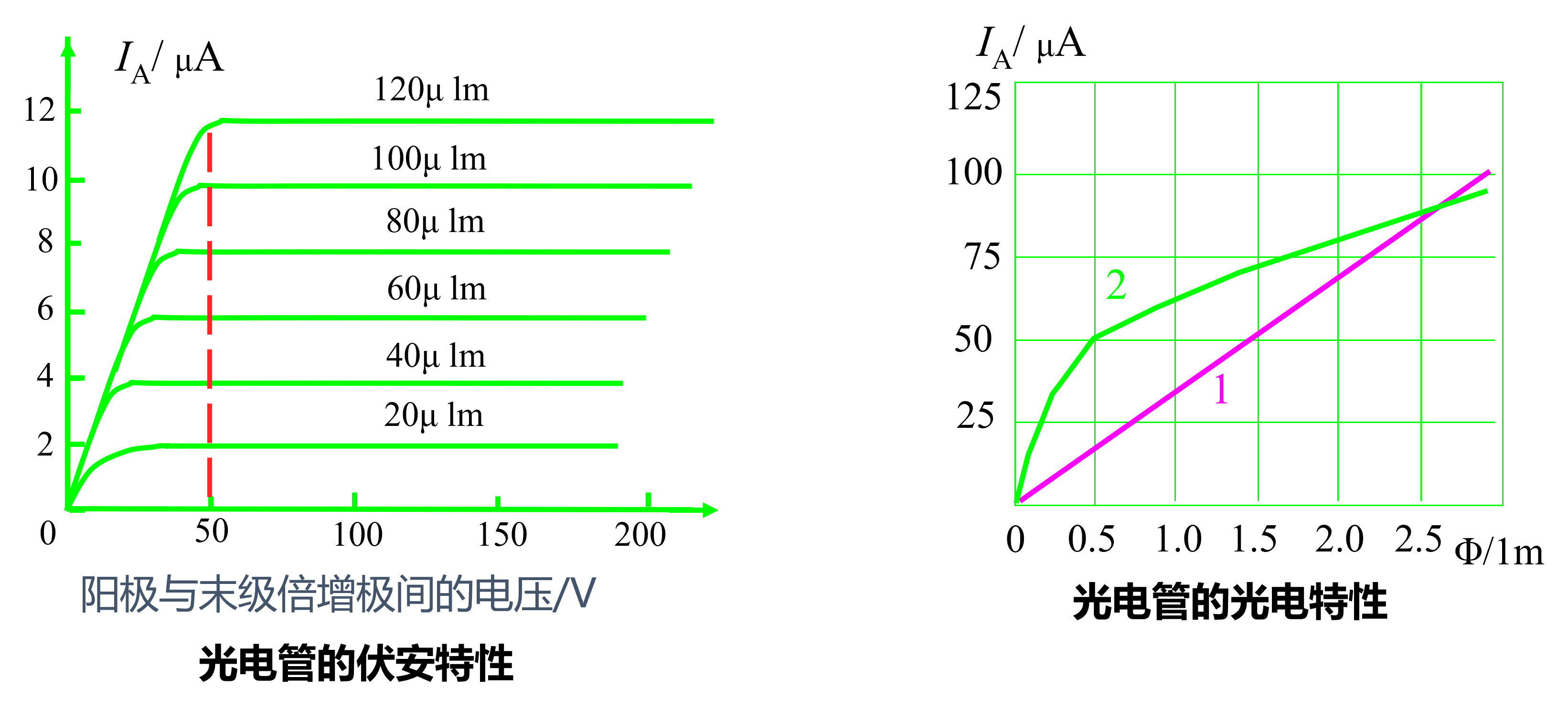
特性

伏安特性：光通量一定时的I-U关系

光电特性：电压一定时，光通量（流明）与光电流的关系

光谱特性：在单位辐照通量（w）下，不同波长的光照射光电管时产生的饱和光电流和光波波长的关系，主要取决于阴极材料

2.3.5.3 光电倍增管

一个阴极，多个阳极

从阴极K上逸出的光电子被第一倍增极D1加速，高速轰击D1，使D1表面逸出更多二次电子，逐级前进，直到最后的阳极A

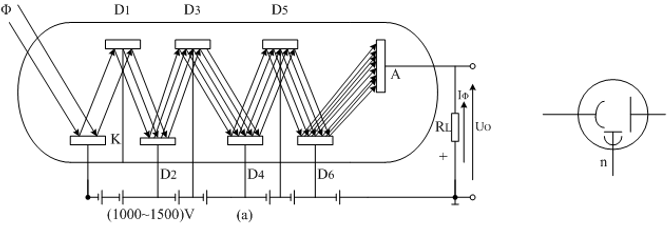
由光阴极K，次阴极（倍增电极Dn），阳极A组成

特性

灵敏度：每单位光通量使阳极产生的饱和光电流（入射一个光子后在阳极上能收集到的平均光电子数目），衡量探测能力；光电倍增管的灵敏度极高，设\(n\)个次阴极，每个次阴极二次电子发射倍增率为\(\delta\)，总共增大\(\delta^n\)倍

光谱特性：对不同频率的入射光的灵敏度，故描述灵敏度时需要指明光波长

暗电流：没有光照，但是有电压时的电流大小，由热发射或场致发射造成，可用补偿电路消除；决定了PMT的可检测光通量的阈值

伏安特性：与光电管类似

磁特性：磁场会使电子轨迹偏移

应用

分光光度计，γ射线探测（pet），各种荧光显微镜的检测端，流式细胞仪

2.3.5.4 光电池

利用光生伏特效应，半导体内部产生光生电动势，可以储能

2.3.5.5 光纤

设纤维芯和覆盖层的折射率分别为\(n_1,n_2\)，角度定义为与光纤轴的偏角（即在界面入射角的余角），定义\(\theta_0\)为临界角，有
\[ \cos{\theta_0} = \frac{n_2}{n_1} \]
定义数值孔径\(N.A. = n_1\sin{\theta_0} = \sqrt{n_1^2 - n_2^2}\)，反应了光纤对入射光的吸收能力，越大越好

为什么这样定义？因为这样的话使得\(N.A.\)与\(\theta_0\)正相关

2.4 压电式传感器

2.4.1 应用

机器人的表面仿生皮肤，拥有了触觉

2.4.2 压电效应

压电效应：一些非中心对称的晶体，在外界压力作用下内部产生极化，在两个表面上产生等量异种电荷；外力消失后，电荷中和；电荷量大小正比于外力大小

逆压电效应：外部附加交变电场产生机械形变

本质上是介质极化产生电偶极矩，一般都是各向异性的晶体

表面电荷密度的公式为
\[ \delta _i = d_{ij} \cdot \sigma _j=d_{ij} \frac{F_j}{A_j} \]
其中\(d_{ij}\)为压电系数，表示在\(j\)方向上受力而在\(i\)方向上产生电荷

2.4.3 常见材料

石英：不是任何方向都有，而且不是很大

钛酸钡：第一个压电陶瓷材料

锆钛酸铅：PZT，性能比钛酸钡好

2.4.4 应用

特点：频带宽，灵敏度和信噪比高，结构简单，工作可靠

压电振子

在材料上铺设激励和接收电极，在激励电极上施加电信号，利用逆压电效应产生机械形变

可以产生位移，也在光电传感器中作为精密微调环节（位移台）

石英微天平

一层吸附膜可以吸附被探测物体，吸附后膜的总质量变化，固有频率改变，引起谐振频率的改变

加入不同频率的交流电可以测量谐振频率

精度很高

2.5 热电式传感器

2.5.1 应用

典型应用是电子体温计和温度报警器

2.5.2 原理

信号转换过程为：温度\(\rightarrow\)电阻\(\rightarrow\)电压

金属热电阻

金属的电阻率随温度变化，经验公式为\(R_T = R_0[1+\alpha(T-T_0)]\)，没啥用

常用材料：铂（稳定，标准，贵）；铜（工业，便宜）；铁，镍（高灵敏）

半导体热敏电阻

一些金属氧化物，分为三类

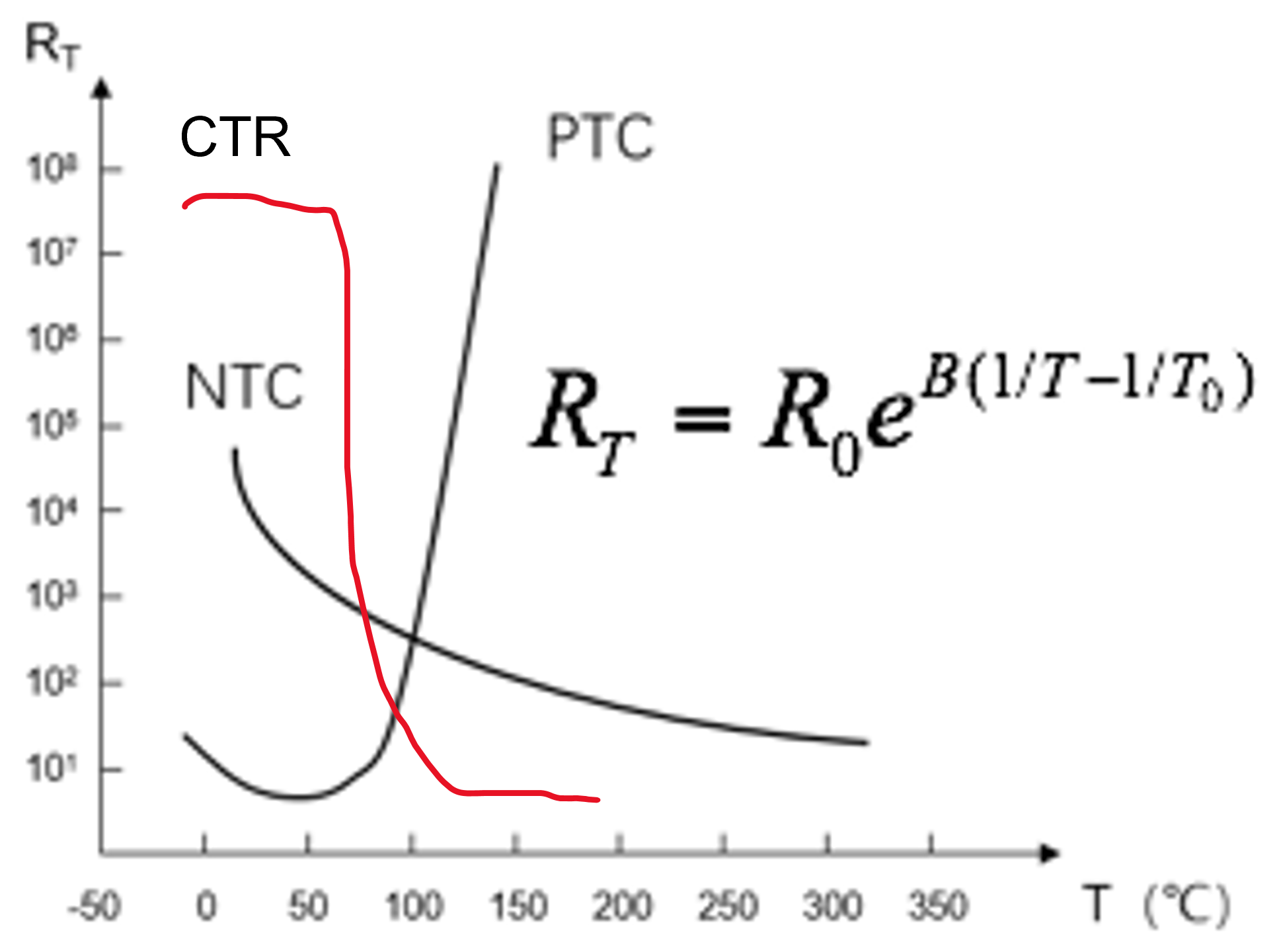
PTC：B<0，可以作为限流元件

NTC：B>0，变化的范围广，测温，线性度好

CTR：在某个临界温度变化极快，灵敏度高，响应快，分辨率高，适合测量微弱的温度变化，但是线性度差

伏安特性

在不同温度下的电压电流曲线

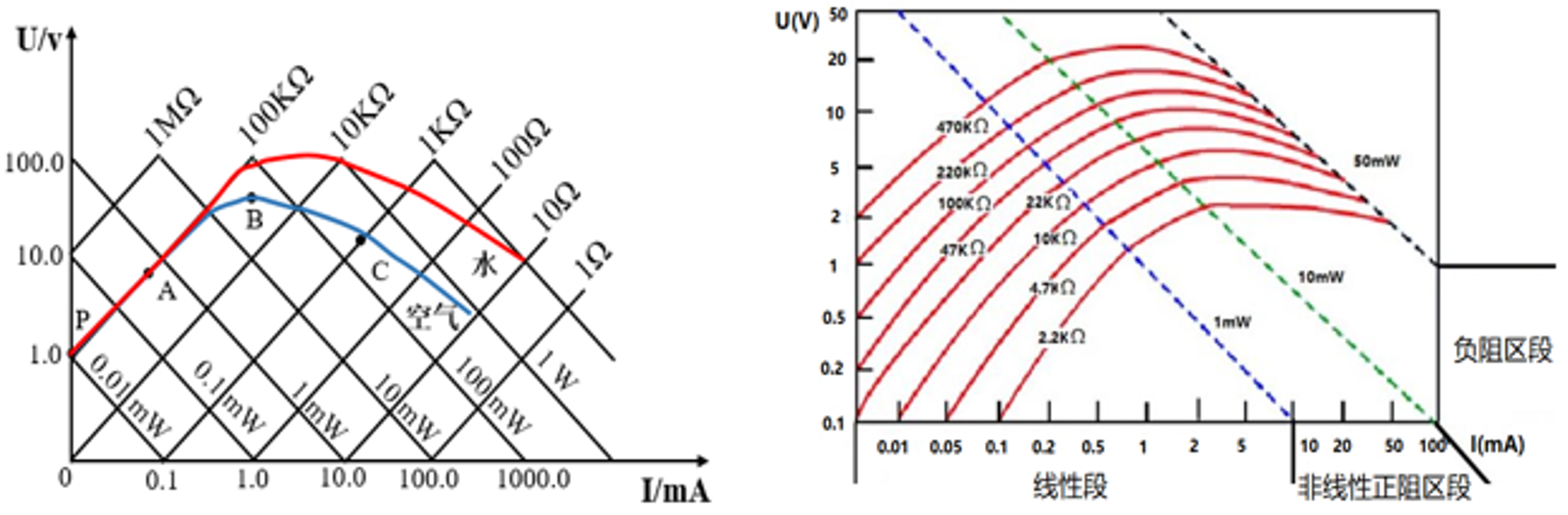
2.5.3 热电偶传感器

两种不同的金属导体组成闭合回路，两端产生温度差，电子的运动产生差异，热运动快的电子扩散向另一端，产生了一个空间电场区

由于是导体，有电势差就有电流

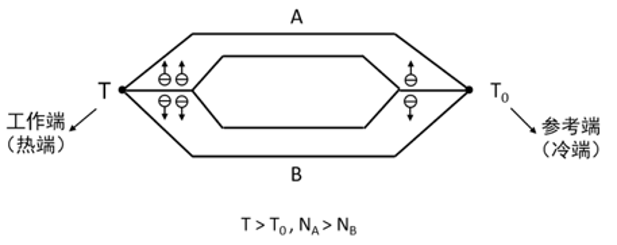
其中参考端的温度已知，根据电流/电势大小可以粗略测量温差

这是一个无源元件，不需要额外供能，结构简单，测量范围宽，但是灵敏度低

响应曲线近似表达为
\[ E_{AB}(T, T_0) = a(T-T_0)+b(T^2-T_0^2) \]

2.5.4 其他热电式传感器

温敏三极管和外围电路集成在一个芯片上，构成独立的温度传感器

热辐射传感器，不同温度的波源产生的热辐射的波长不同，在内部存在一个热电偶堆，热电偶串联，电势加强

总结起来，热电式传感器的工作原理如下

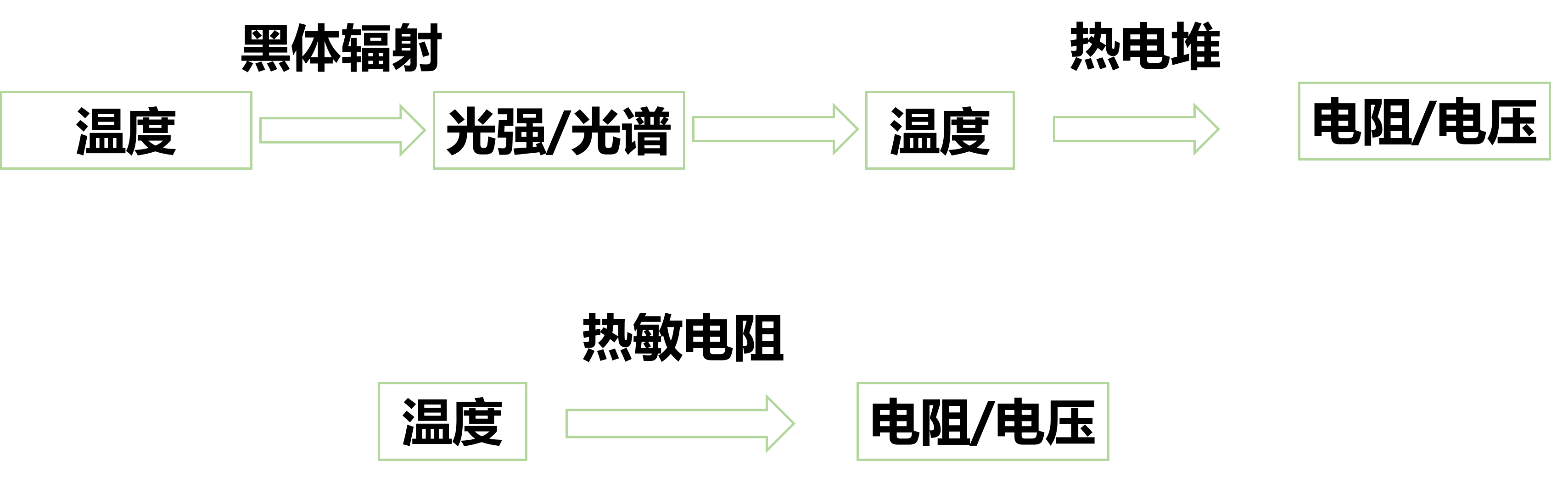
几种热电式传感器对比

热敏电阻：

原理：半导体材料的电阻随温度变化，主要因素是载流子浓度和迁移率随温度的变化关系
温度变化特性：分为三类，但都是非线性
1. 负温度系数（NTC）热敏电阻，随温度上升，电阻值减小
2. 正温度系数（PTC）热敏电阻，随温度上升，电阻值增加
3. 临界温度系数（CTR）热敏电阻，当温度升高到某临界点时，电阻值突然下降
测量范围：相对来说最小
灵敏度：相对来说最高
精度：三者的中间水平

RTD热电阻：

原理：由线圈或纯金属沉积膜组成，电阻以已知且可重复的方式随温度变化
温度变化特性：几乎是纯线性，正温度系数
测量范围：三者的中间水平
灵敏度：三者的中间水平
精度：相对来说最高

热电偶：

原理：当热电偶的两端处于不同温度时，两种不同的金属的连接产生可测量的电压
温度变化特性：非线性
测量范围：相对来说最大
灵敏度：相对来说最低
精度：相对来说最低