10 IIR滤波器的设计
10.1 基本设计思路
- 首先需要给定IIR数字滤波器的技术指标,如\(\omega_p,\omega_{st},A_p,A_{st}\)分别是通带截止频率,阻带截止频率,通带衰减和阻带衰减
- 根据数字指标,转换为模拟指标
- 根据模拟指标得到模拟低通滤波器的技术指标,也就是归一化
- 查表,通过模拟低通的原型计算模拟滤波器的表达式
- 将模拟滤波器转换为数字滤波器
可以看到AD/DA各一次;有两种方法
10.2 冲激响应不变法
基本想法
对得到的模拟滤波器进行抽样,得到数字滤波器,即
- 已知\(H_a(s)\),逆变换得到\(h_a(t)\)
- 对其采样,得到\(h(n)=h_a(nT_s)\)
- 做Z变换得到数字滤波器\(H(z)\)
如果
\[
H_a(s) = \sum\frac{A_k}{s-s_k}
\]
那么最终得到的
\[
H(z)=\sum\frac{A_k}{1-e^{s_k T_s}z^{-1}}
\]
证明略,好证的
本方法对第1-4步延续了传统的想法,即
- \(\Omega=\frac{\omega }{T_s}\),\(A_p,A_{st}\)不改变
- 设计低通模拟滤波器系统函数\(H_a(s)\)
- 用上面的方法将\(H_a(s)\)转换为\(H(z)\)
方法的局限
由于使用了抽样,这必然会导致一个抽样定理的问题,即
\[
z=e^{sT}\Rightarrow z=e^{\sigma T}e^{j\Omega T}\Rightarrow r=e^{\sigma T},\omega=\Omega T
\]
由于\(\omega\in[-\pi,\pi]\),这会导致映射非双射,表现在系统函数上就是,在\(\Omega=\pm\frac{\pi}{T}\)之外的频谱会造成混叠
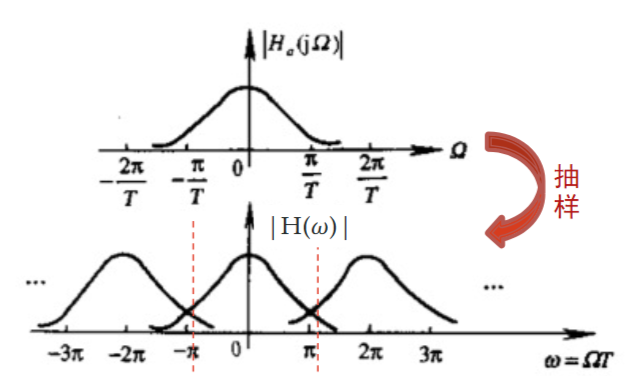
用抽样定理的视角来看,\(\omega\)的周期为\(2\pi\),那么对\(\Omega\)的抽样频率就是\(\frac{2\pi}{T}\),即折叠频率就是\(\frac{\pi}{T}\)
这带来的问题就是:高通/带阻滤波器无法设计。因为实际中无法限制模拟滤波器的频谱
特点
- 频率变换是线性的,即\(\omega=\Omega T\)
- 时域的逼近程度好,毕竟是对其进行采样的
- 周期延拓问题
10.3 双线性变换法
为了构造单一的频率映射而出现,直接给出映射公式
\[
s=\frac{2}{T_s}\frac{z-1}{z+1}
\]
那么在频率响应上,即\(z=e^{j\omega}\)上,这个映射就是
\[
\Omega = \frac{2}{T}\tan{\frac{\omega}{2}}
\]
基本想法
- 根据数字滤波器的技术指标要求,通过\(\Omega = \frac{2}{T}\tan{\frac{\omega}{2}}\)得到模拟指标
- 根据模拟指标和模拟滤波器原型设计模拟滤波器,得到\(H_a(s)\)
- 用\(s=\frac{2}{T_s}\frac{z-1}{z+1}\)带入\(H_a(s)\),得到\(H(z)\)
通过原型设计模拟滤波器
一个例子如下
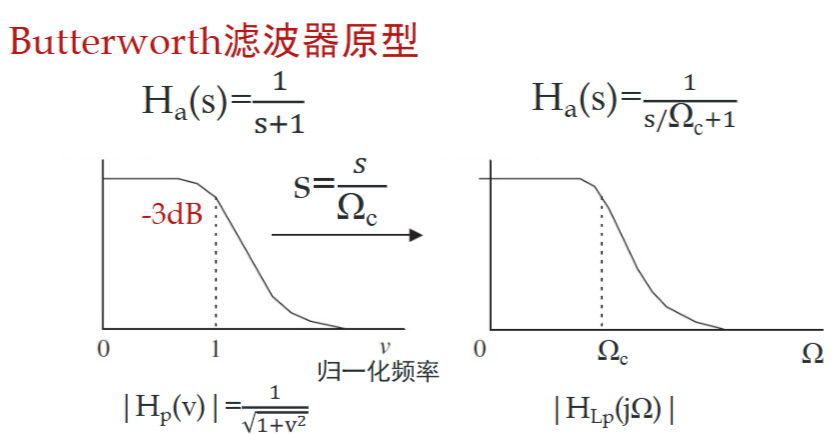
转换为其他类型的滤波器的方法如下
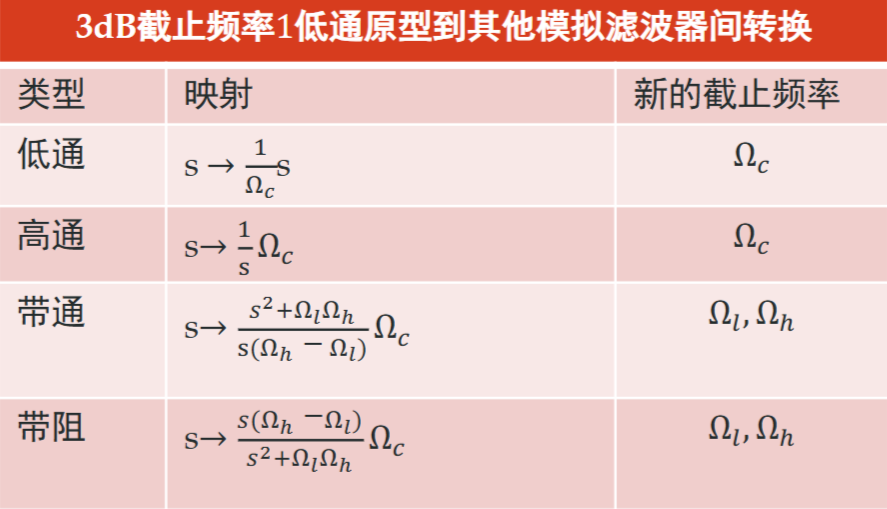
对这张表的修正:低/高通的\(\Omega_c\)变为\(\Omega_p\),带通/阻的\(\Omega_c\)变为1,\(\Omega_l/\Omega_h\)指的是通带截止频率
原型滤波器的设计
存在两种,巴特沃兹和切比雪夫
- 巴特沃兹,通带平坦但是过渡带宽大;需要指的滤波器的阶数
已知n阶低通巴特沃兹的表达式为
\[
|H_p(\nu)|=\frac{1}{\sqrt{1+\varepsilon^2\nu^{2n}}}
\]
其中\(\nu\)是归一化模拟角频率,当\(\nu=\nu_p=1\)时为通带截止频率,即
\[
A_p = 20\lg{\frac{1}{\sqrt{1+\varepsilon^2}}} \Rightarrow \varepsilon^2=10^{-\frac{A_p}{10}}-1
\]
当\(\nu=\nu_s\)时为归一化阻带截止频率,即
\[
A_{st} = 20\lg{\frac{1}{\sqrt{1+\varepsilon^2\nu_s^{2n}}}}
\]
\(\nu_s\)有
\[
\nu_s = \frac{\Omega_{st}}{\Omega_p}
\]
利用\(A_p,A_{st},\nu_s\)的值,求得n为
\[
n \geq \left(\lg{\frac{10^{-0.1A_{st}}-1}{\varepsilon^2}}\right)/(2\lg \nu_s)
\]
特别的,当\(A_p=-3\)dB时,\(\varepsilon=1\)
不同阶的滤波器原型会在考试中给出
- 切比雪夫,通带波纹大,但是过度带宽小,这个就不赘述了估计不会考,直接给结果
\[ \varepsilon^2 = 10^{-0.1A_{p}}-1 \]
\[ n\geq \cosh^{-1}\left( \frac{10^{-0.1A_{st}}-1}{\varepsilon^2} \right)^2/\cosh^{-1}\nu_s \]
例:设计一个低通IIR滤波器,满足截止频率为\(f_p=\)1.5kHz,通带衰减-\(A_p\)3dB,阻带频率\(f_{st}=\)3kHz,阻带衰减\(A_{st}=\)-10dB;抽样频率8000Hz
解:首先求截止频率的模拟角频率
\[
\Omega_p=\frac{2}{T_s}\tan(2\pi f_p/f_s/2)=1.07\times10^{4}
\]
\[ \Omega_{st}=\frac{2}{T_s}\tan(2\pi f_{st}/f_s/2)=3.86\times10^{4} \]
那么归一化的阻带截止频率就是
\[
\nu_s = \frac{\Omega_{st}}{\Omega_p} = 3.613
\]
带入上文公式,得到\(\varepsilon=1,n\geq0.855\),取\(n=1\),即原型为
\[
H_a(s) = \frac{1}{s+1}
\]
由于是求的低通,故用\(S = \frac{s}{\Omega_p}\)带入,得到
\[
H_{LP}=\frac{1}{s/\Omega_p+1}
\]
再经过变换得到\(H(z)\)
10.4 IIR与FIR的对比
- IIR
- 准确的边缘频率
- 利用模拟滤波器设计,有大量轮子用
- 存在反馈,阶数更少
- 缺点:相位非线性;存在右边极点,系统条件稳定
- FIR
- 严格的线性相位
- 系统一定是稳定的
- 可以用FFT快速计算
- 缺点:截止频率难控制