9 FIR滤波器的设计
数字滤波器就是一个系统,可以用迄今为止所有对系统的描述方式对其进行描述
9.1 数字滤波器的分类
根据是否有限,分为FIR和IIR两种,二者的框图如下
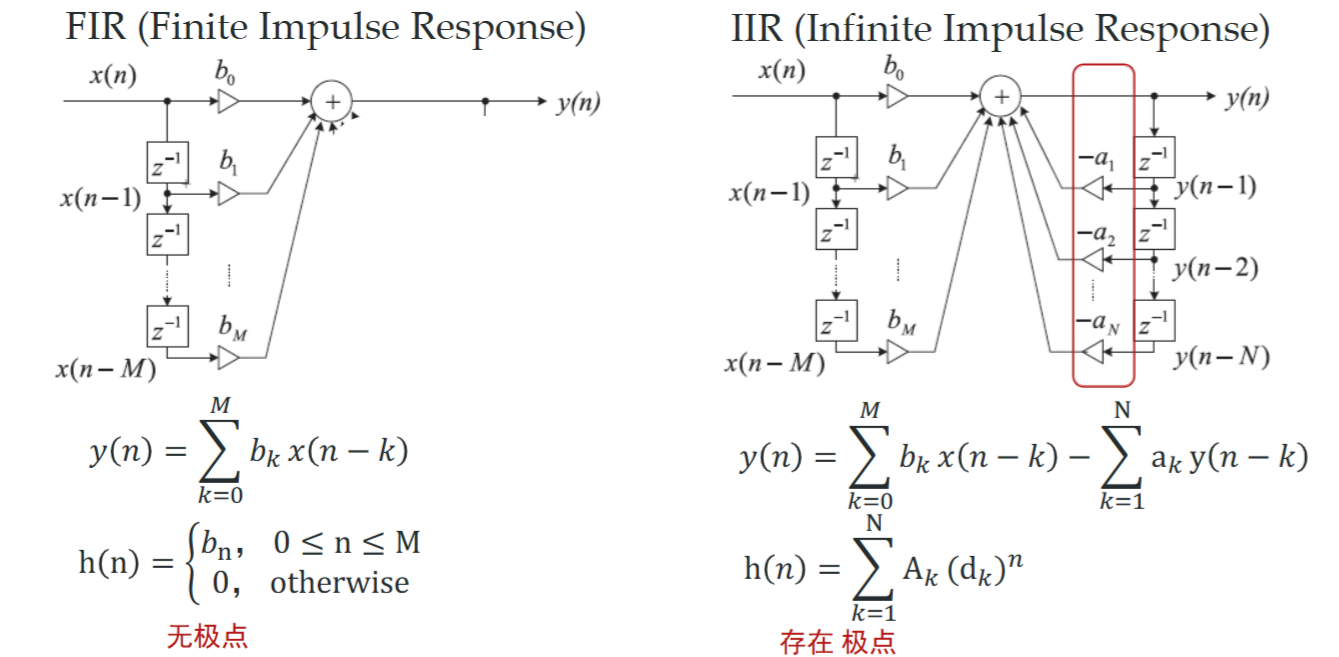
显然FIR滤波器是一定稳定的,IIR滤波器存在极点而是条件稳定
9.2 FIR滤波器的基本结构
输入输出关系为
\[
y(n) = \sum_{i=0}^K b_i x(n-i) = \sum_{i=0}^K h(i) x(n-i) = h(n) * x(n)
\]
其中
\[
h(n) = \begin{cases}
b_n\,\,,\,\, 0\leq n \leq K\\
0\,\,\, ,\,\,\, o.w.
\end{cases}
\]
几个性质
- 由于是有限的,可以使用FFT/DFT
- 系统函数是稳定的
- 有严格的线性相位
例:

这是一个滑动窗口,用于信号的去噪平滑
非理想数字滤波器的性能参数
由于物理系统的限制,不可能做到理想的滤波器,一个典型的物理上能实现的滤波器如下
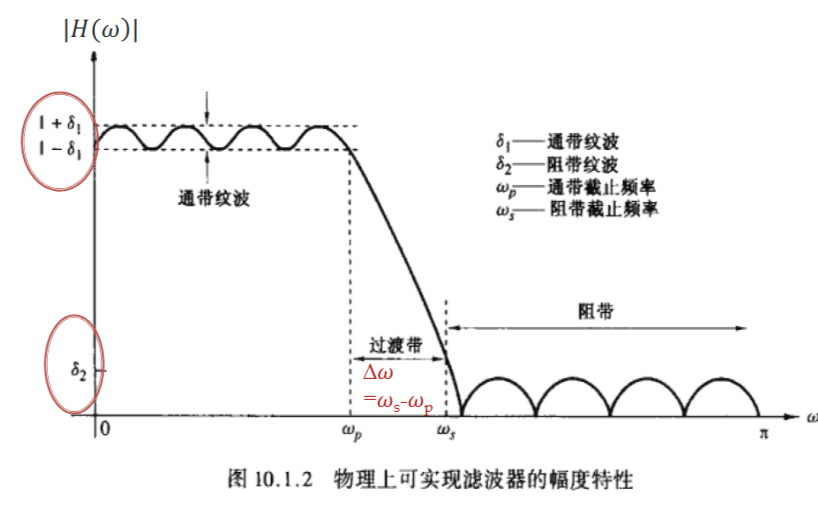
通常采用分贝表示各个波纹大小(\(20\lg \))
- \(\delta_1\)是通带波纹
- \(\delta_2\)是阻带波纹
- \(\omega_p\)是通带截止频率
- \(\omega_s\)是阻带截止频率
这些是怎么产生的?
很显然不可能有无限长的时域\(\mathsf{sinc}\)函数,必须加窗,相当于在频域内的窗函数卷积一个\(\mathsf{sinc}\)
卷积的结果是sinc在窗内的面积和,即
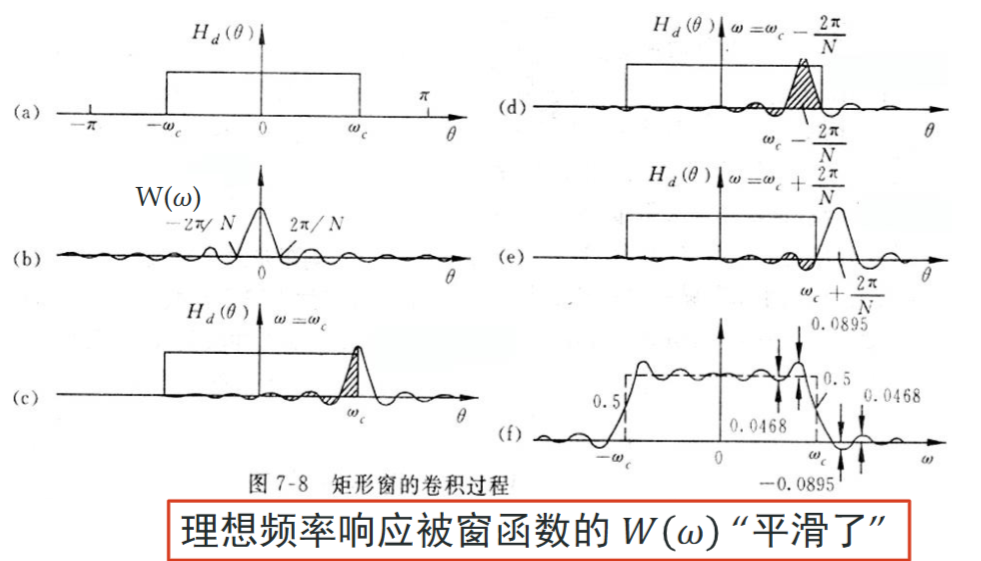
那么\(\delta_1,\delta_2\)产生自sinc的旁瓣,\(\omega_p,\omega_s\)产生自规定的通频带分别减/加与滤波器窗长度\(N\)反相关的量
值得一提的是,在我们希望的截止频率\(\omega_c\)处,\(H_d(\omega_c)=0.5\)恒成立
9.3 窗函数法设计FIR滤波器
如上所述,对时域的sinc函数加窗产生一个非理想的频域窗函数,步骤如下
对于\(h(n)=\mathsf{sinc}(n)\),使用\(w(n)=\begin{cases} 1,|n|\leq M\\0,o.w. \end{cases}\)截断,产生物理上可实现的有限长信号\(h_d(n)=h(n)w(n)\)
对\(h_d(n)\)做DFT/FFT,得到的就是\(H_d(\omega) = \frac{1}{2\pi}(H(\omega)*W(\omega))\)
在频域中验证\(H_d(\omega)\)的上述参数是否满足要求,如果满足了就继续操作\(h_d(n)\)
因为物理系统一定是因果的,故需要对\(h_d(n)\)进行平移,得到\(h_d^{'}(n) = h_d(n-M)\)
最终得到的是时域上的信号,这是要产生的信号所以必须是时域的
由于最终结果都是一个频域的窗,故时域的模板是已知的,都是
\[
h(n) = \begin{cases}\
\frac{\omega_c}{\pi} \,\,,\,\, n=0\\
\frac{\sin{\omega_c n}}{n\pi}\,\,,\,\, |n|\leq M ,n\neq 0
\end{cases}
\]
其中\(\omega_c\)是希望的截止频率
同上述关系,窗函数\(W(\omega)\)的主瓣宽度正相关于滤波器的过渡带宽\(\Delta \omega\),\(\delta_1,\delta_2\)产生自sinc的旁瓣
例:窗函数法设计3阶低通滤波器,截止频率\(f_c=800\)Hz,抽样频率\(f_s=8000\)Hz
解:首先需要有数字频率和模拟频率的关系,数字为\(\omega\)
\[
\omega = \Omega T_s
\]
这个可以用\(x(nT_s) = x(t)\)理解,\(\omega = \frac{2\pi}{n},\Omega=\frac{2\pi}{t}=\frac{2\pi}{nT_s}\)
那么模拟截止频率为\(f_c\),数字截止角频率\(\omega_c = 2\pi f_c /f_s = 0.2\pi\)
带入通式,得到\(h(0)=0.2,h(1)=0.1871,h(-1)=0.1871\),还需要进行平移,最终得到
\[
h(0) = 0.1871, h(1)=0.2,h(2)=0.1871
\]
对其做\(Z\)变换,得到
\[
H(z) = \sum h(n)z^{-n}=0.1871 + 0.2z^{-1}+0.1871z^{-2}
\]
但是,实际进行画图发现,这个滤波器的截止频率大致在2600Hz,原因在于窗太小,如上所述
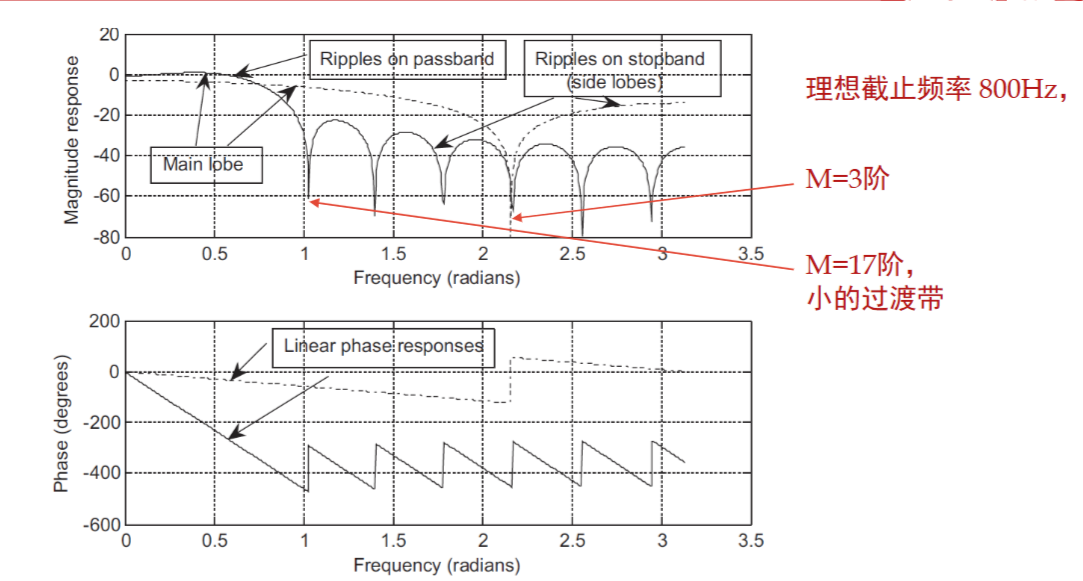
滤波器的实际截止频率\(\omega_s\)是与时域窗函数截断的长度\(M\)反相关的
理想滤波器的原型
低通
\[ h(n) = \begin{cases}\ \frac{\omega_c}{\pi} \,\,,\,\, n=0\\ \frac{\sin{\omega_c n}}{n\pi}\,\,,\,\, |n|\leq M ,n\neq 0 \end{cases} \]高通,理解为1-低通
\[ h(n) = \begin{cases}\ \frac{\pi-\omega_c}{\pi} \,\,,\,\, n=0\\ -\frac{\sin{\omega_c n}}{n\pi}\,\,,\,\, |n|\leq M ,n\neq 0 \end{cases} \]带通,理解为两个低通相减
\[ h(n) = \begin{cases}\ \frac{\omega_H - \omega_L}{\pi} \,\,,\,\, n=0\\ \frac{\sin{\omega_H n}}{n\pi}-\frac{\sin{\omega_L n}}{n\pi}\,\,,\,\, |n|\leq M ,n\neq 0 \end{cases} \]带阻,理解为1-带通
\[ h(n) = \begin{cases}\ \delta(n)-\frac{\omega_H - \omega_L}{\pi} \,\,,\,\, n=0\\ -\frac{\sin{\omega_H n}}{n\pi}+\frac{\sin{\omega_L n}}{n\pi}\,\,,\,\, |n|\leq M ,n\neq 0 \end{cases} \]
注意,这些都还需要右移\(M\),变成因果系统
一般性窗
除了矩形窗之外,还有别的窗可以选择
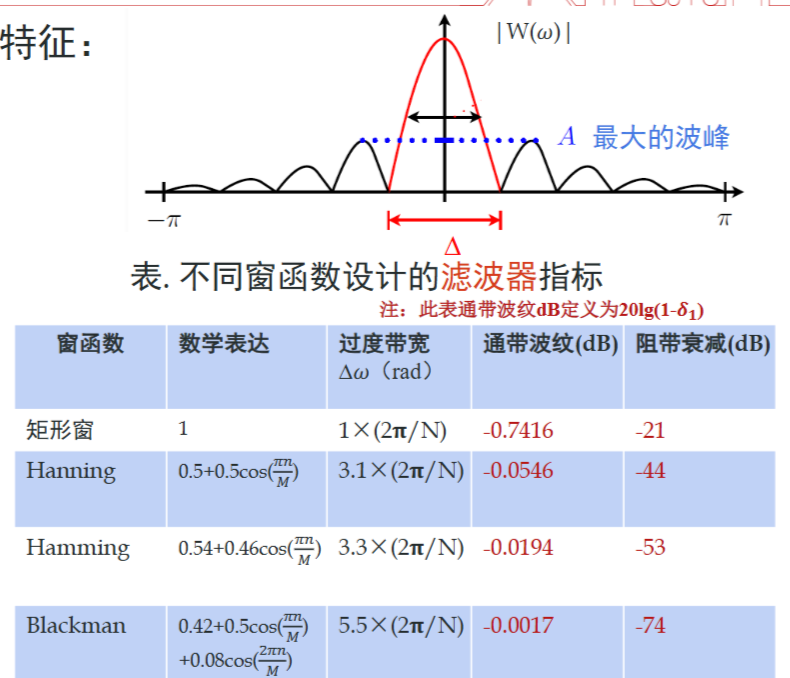
根据要求选择合适的窗,注意,还需要点乘辛格函数
一般而言,窗函数的图像有以下性质,规定长度\(N=2M+1\)
- \(N\cdot \Delta = Const\),因此,窗越宽,滤波器越理想
- \(|A|\)取决于窗的类型,与\(N\)无关
- \(A\)与\(\Delta\)通常反相关,需要trade-off(这里指的是改变了窗函数的类型,时域越平滑的窗函数高频成分越少,A小Δ大)
- 矩形窗的主瓣和造成的过渡带宽更小(其实是一个东西),但是有更大的旁瓣
FIR滤波器的特点
- 优点:线性相位;创造的方法简单
- 缺点:不容易控制边缘频率,显然不能做到精准的\(\omega_c\);即使精准了,\(h(n)\)往往很长
设计步骤
- 根据阻带衰减要求和过渡带宽,选择窗函数的类型
- 根据过渡带宽确定理想滤波器的截止频率,根据窗函数的特性确定窗的长度\(N\)
- 平移滤波器,得到因果的系统
- 根据\(h(n)\)再求\(H(\omega)\),看是否满足要求
例:抽样频率8000Hz,通带要求0-800Hz,阻带1000-4000Hz,通带波纹-0.02dB,阻带衰减-50dB
解:根据上面的表格,hamming和blackman都能满足,选择hamming
过渡带宽\(\Delta \omega = 2\pi \times (1000-800)\div 8000 = 0.05\pi = 3.3\times2\pi\div N\),得到窗长\(N\geq 132\),取\(N=133\)
为什么?下面会讲
截止频率就是通带频率和阻带频率的中间值,即\(\omega_c = \frac{\omega_s+\omega_p}{2}=2\pi\times 900\div 8000\),用这个算理想滤波器的时域表达式,然后二者相乘得到滤波器表达式
将\(M = \frac{N-1}{2}\)带入滤波器的表达式,平移,得到结果
不同类型的FIR滤波器的适用情况
存在以下四种线性相位的FIR滤波器
| 情况i | h(n) | N | 适用情况 |
|---|---|---|---|
| 1 | h(n) = h(N-1-n) | 奇数 | 全能 |
| 2 | h(n) = h(N-1-n) | 偶数 | 低通,带通 |
| 3 | h(n) = -h(N-1-n) | 奇数 | 带通 |
| 4 | h(n) = -h(N-1-n) | 偶数 | 高通,带通 |
9.4 频率抽样法设计FIR滤波器
基本想法是根据理想滤波器的\(N\)个点确定实际FIR滤波器的DFT,然后做iDFT得到满足这些点的\(h(n)\)
即,给定理想的\(H_d(\omega)\),进行采样,使得\(|H(k)| = |H_d(\omega)|_{\omega= \frac{2\pi}{N}k}\),其中\(k=0,1,\ldots,N-1\)
然后得到\(h(n) = \mathsf{iDFT}\{H(k)\}\)
为了得到线性相位的滤波器,辐角必须是
\[
\varphi(\omega) = -\left(\omega\frac{N-1}{2}-\beta\right)
\]
其中当\(h(n)\)奇对称时\(\beta=\frac{\pi}{2}\),偶对称时\(\beta=0\)
对于\(H(k)\),将\(\omega\)换成\(\frac{2\pi}{N}k\),带入iDFT的公式
对于\(h(N-1-n)=h(n), N=2M+1\)的滤波器
\[
h(n) = \frac{1}{N}\left[H(0)+2\sum_{k=1}^{M}|H(k)|\cos\left(\frac{2\pi k(n-M)}{N}\right)\right]
\]
其中\(M = \frac{N-1}{2}, n=0,1,\ldots,N-1\),用到了\(H^*(k)=H(N-k)\)
对于\(h(N-1-n) = h(n),N=2M\)的滤波器,则
\[
h(n) = \frac{1}{N}\left[H(0)+2\sum_{k=1}^{M-1}|H(k)|\cos\left(\frac{2\pi k}{N}\left(n-\frac{N-1}{2}\right)\right)\right]
\]
其余见下图


关于II型的说明:图片不好更改,但是根据DFT的定义,代入\(N=2M\)可以得到\(H(M)\)
\[
H(M) = \sum_{n=0}^{2M-1}h(n)e^{-j\frac{2\pi}{N}Mn} = \sum_{n=0}^{2M-1}h(n)(-1)^{n}
\]
根据\(h(n)=h(2M-1-n)\),因为\(n\)和\(2M-1-n\)奇偶性显然不同,故\(h(n)(-1)^n+h(2M-1-n)(-1)^{2M-1-n}=0\)
所以\(H(M)=0\),因此图上II的\(H_M\)可以舍去
不过一般设计都是I型
整个设计流程就是
- 根据\(H_d(\omega)\)确定FIR滤波器的类型(高/低通等),长度\(N\)和幅度\(|H(k)|\)
- 根据实际情况确定线性相位的\(\beta\)
- 在\([0,2\pi]\)上采样\(N\)个\(H_d(\omega)\),注意中间的是高频,得到\(|H(k)|\)
- 根据\(|H(k)|e^{j\varphi(k)}\)进行iDFT,得到\(h(n)\),不用平移,因为这个相位就是平移后的
例:已知\(H_d(\omega)\)是\(\omega_c=\frac{3\pi}{4}\)的理想低通FIR滤波器,使用抽样法设计\(h(n)\),抽样间隔为\(\frac{\pi}{2}\)
解:\(\Delta \omega=\frac{2\pi}{N} = \frac{\pi}{2}\Rightarrow N =4\),那么由于是低通,必须选择情况2,不能用情况4,\(\varphi = -\frac{3}{2}\omega\)
\(|H(k)|\)则为\(H(0)=H(1)=H(3)=1,H(2)=0\),那么这个序列就确定了,iDFT得到\(h(n)\)
\[
h(n) = \frac{1}{4}[1+2\cos\frac{\pi}{2}(n-1.5)]
\]
改进
上面的方法存在问题,在通带的1直接跳到阻带的0,引入了非常大的高频分量,导致阻带衰减不够低
由于阻带衰减与窗的长度无关,增加采样点不能解决问题
只能减小这个高频分量,也就是在1和0之间加0.5,平滑这个跳变
在数学上相当于对这个跳变进行插值,也就是在2.3节提到的内插辛格函数
一般情况下,不增加过度点的阻带衰减大致为-21dB,增加一个过渡点是-65dB,两个则是-75dB
相对于窗函数法的优势
- 当\(H_d(\omega)\)没有数学表达式时
- 增加过渡点,阻带衰减能很小
- 截止频率更准确
缺点
- 抽样频率间隔固定
- 截止频率自由的前提增加抽样点,导致计算成本大