8 FFT
8.1 为什么有FFT
首先是DFT带来的问题
频谱泄露
当截取小片段时,相当于使用了一个长度为\(L\)的窗,其DTFT是一个主瓣宽度为\(\frac{4\pi}{L}\)的\(\mathsf{sinc}\)函数
这样会引入杂波,如下图
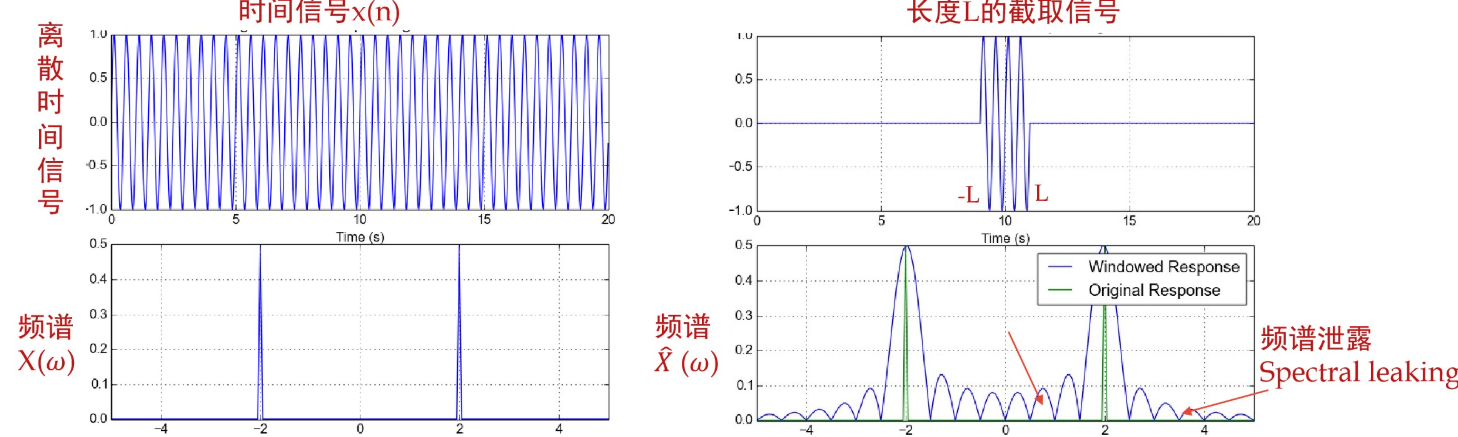
当主瓣很宽时,两个相邻的冲激峰就会重叠,定义当sinc的0点恰好在另一个峰的频率时,两个峰不可辨认
即要求
\[
\frac{2\pi}{L} \leq \min\{\omega_i-\omega_j\}
\]
故小序列不是能无限小的
例:\(x(n)=\cos\omega_0 n+\cos\omega_1 n+\cos\omega_2n\),其中\(\omega_0=0.2\pi,\omega_1=0.22\pi,\omega_2=0.6\pi\),求序列最短能是多少
解:带入上面的公式,得到\(L_{\min}=100\)
DFT对频谱分辨率的影响
根据定义,\(\omega_k = \frac{2\pi k}{N}\),那么\(\Delta \omega=\frac{2\pi}{N}\)就是\(X(k)\)在频域的分辨率
为了将DTFT的两个峰\(|\omega_1-\omega_2|\)在DFT中分开,需要有
\[
\Delta \omega \leq \min\{\omega_1-\omega_2\}
\]
计算量
由于\(X(k)\)的计算都是复数计算,根据公式\(N\)个序列的DFT计算量为\(O(N^2)\)
这是NP问题的时间复杂度,非常不好
由此,引出了FFT
8.2 FFT的改善思路
首先需要明确,FFT不是一种新的计算,没有物理意义;它只是DFT的一个快速算法
关键思路
关键在\(W_N^k = e^{-j\frac{2\pi}{N}k}\)
对称性:
\[ W_N^{k+\frac{N}{2}} = -W_N^{k} \]周期性:
\[ W_N^{k+N} = W_N^{k} \]
预处理:\(x(n)\)的长度\(N\)通过补0,到最近的\(2^M\)
将\(x(n)\)分为奇偶序列,\(x_1(r)=x(2r),x_2(r)=x(2r+1),r=0,1,\ldots,\frac{N}{2}-1\)
那么
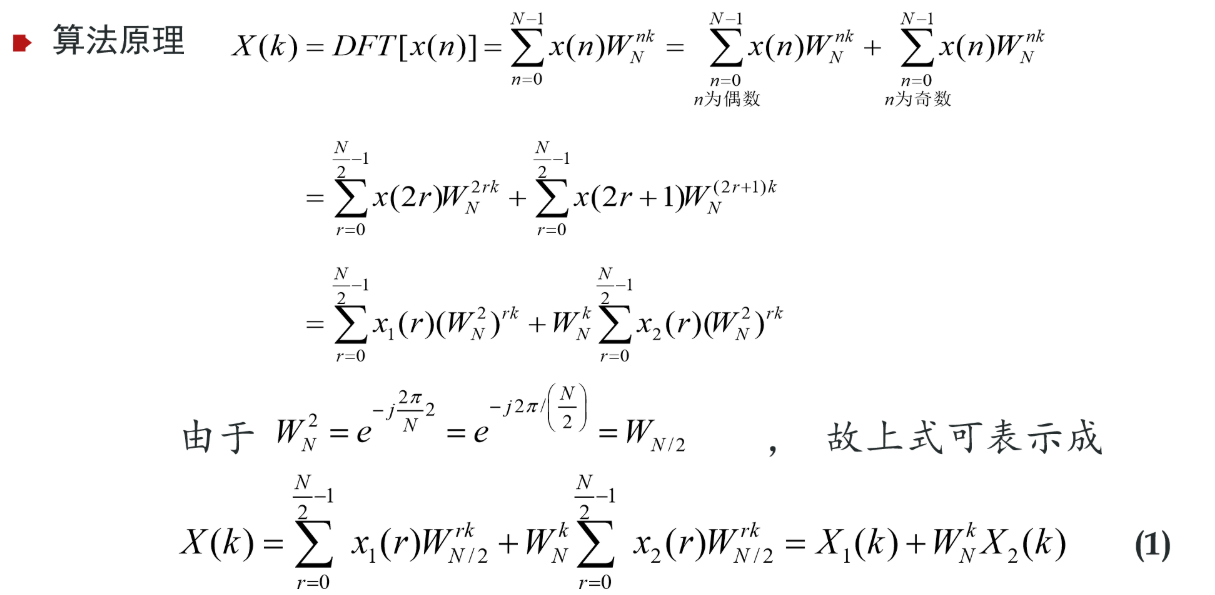
其中\(X_1,X_2\)分别是\(x_1,x_2\)的前\(N/2\)个点的DFT,根据周期性,\(W_{N/2}^{k+N/2}=W_{N/2}^k\)
那么
\[
X_1(k+N/2) = X_1(k)\\
X_2(k+N/2) = X_2(k)
\]
两部分的\(X_i(k)\)是相等的
那么得到
\[
X(k) = X_1(k) + W_N^k X_2(k)\\
X(k+N/2) = X_1(k) - W_N^k X_2(k)
\]
这样就将计算DFT的时间复杂度降为了\(O(N^2/2)\),因为只算了一半的序列
输出的线路图如下
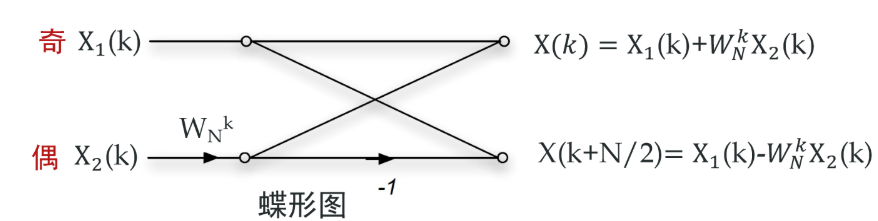
将\(X_1(k),X_2(k)\)视为新的\(X(k)\),上面的算法完全适用,因此一开始需要将\(N\)scale到\(2^M\),就是为了一级级减半
最终可分出\(M\)级蝶形图,一个蝴蝶图的运算时间是\(O(1)\),就只有2次加法和1次乘法
每级一共N/2个蝶形图,需要的运算时间是\(O(N/2)\),一共\(\log_2N\)级,总共花了\(\frac{N\log_2N}{2}\)的时间,相比于DFT提升了\(\frac{2N}{\log_2N}\)倍
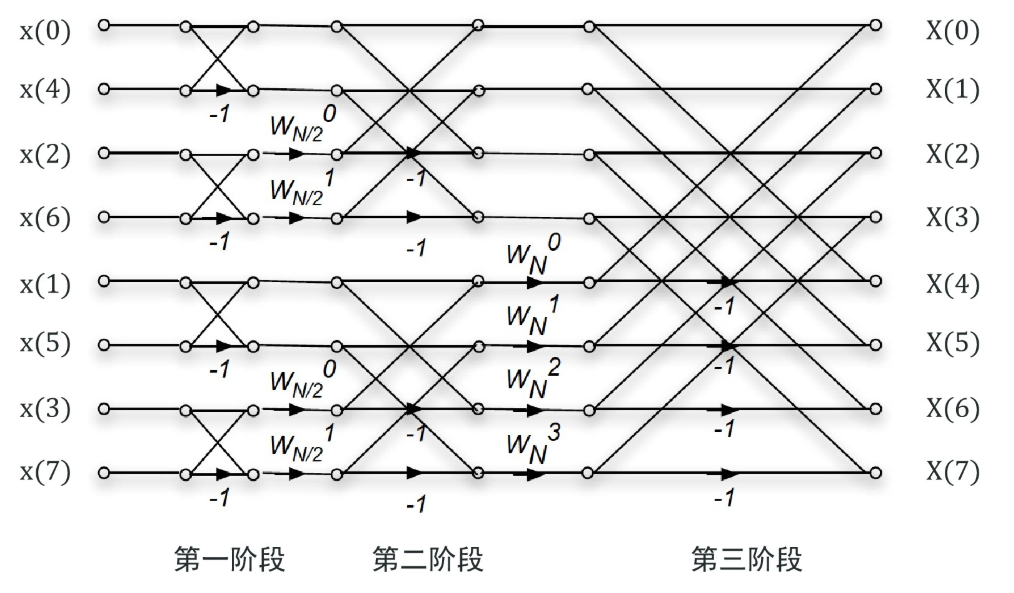
如何计算输入序列的排列
| 原始排列 | 二进制 | 翻转二进制 | 输入序列 |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| 7 | 111 | 111 | 7 |