7 DFT
7.1 DFT的概念
在离散信号经过DTFT后,得到的频谱是连续的,但是数字信号需要离散的表达,由此引出了离散傅里叶变换DFT
DFT表现为对\(X(\omega)\)进行抽样,表达为
\[
X(k)=X(\omega)|_{\omega=\frac{2\pi}{N}k}\,\,\,, k=0,1,\ldots, N-1
\]
其中\(N\)是有限长时域信号的长度,因此
\[
X(k)=\sum_{n=0}^{N-1}x(n)e^{-j\frac{2\pi}{N}kn}
\]
令\(W_N=e^{-j\frac{2\pi}{N}}\)对上式展开,可以发现
\[
X(0)=x(0)+x(1)+\ldots+x(N-1)\\
X(1)=x(0)+x(1)W_N+x(2)W_N^2+\ldots+x(N-1)W_N^{N-1}\\
\ldots\\
X(N-1) = x(0)+x(1)W_N^{N-1}+\ldots+x(N-1)W_N^{(N-1)(N-1)}
\]
因此,可以使用矩阵简化计算,得到

为了得到逆变换,可以假设\(x=AX\),带入DFT,得到
\[
X=Wx=WAX
\]
故\(WA=I\Rightarrow A=W^{-1}\),得到逆变换为
\[
x(n)=\frac{1}{N}\sum_{k=0}^{N-1}X(k)W_N^{-nk}
\]
矩阵如下
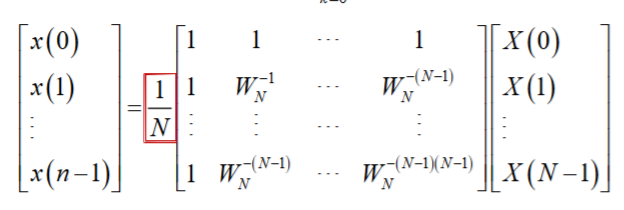
注意,DFT变换对应该有同样的长度
7.2 几个变换的区别
DTFT,DFT,DFS
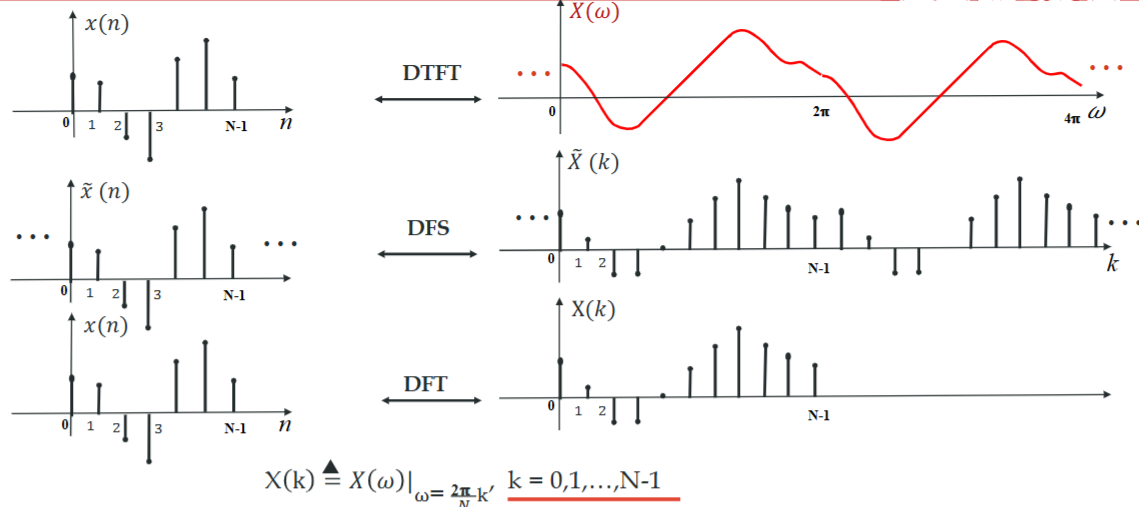
其中\(\tilde{x}\)是周期信号,对周期信号的DFT称为DFS
DFT和DFS没有本质区别,前者是后者的主值区间,后者是前者的周期延拓
DTFT,DFT,Z
容易得到
\[
X(k)=X(z)|_{z=e^{j\frac{2\pi}{N}k}}=X(\omega)|_{\omega=\frac{2\pi}{N}k}
\]
7.3 补零,用于信号分析
当想要的\(X(k)\)序列更加密集时,需要增大\(N\)的值,此时需要对\(x(n)\)进行添0处理,即
\[
x^{'}(n)=\
\begin{cases}
x(n)\,\,\,, n
注意:
- 补零对DTFT无影响,很显然0对累和无效果
- 对DFT来说,只是增加了采样点,整个信号的包络依然是DTFT的图像
- 对于周期信号,只有信号的长度是周期的整数倍,DFT的频谱才不会丢失峰值信息
7.4 DFT的性质
圆周位移
序列的圆周位移的DFT,等价于其周期延拓的线性位移后主周期内的DFT
简单理解就是转过头了就取模
线性
易证
序列共轭
\[
x^*(n) \leftrightarrow X^*(N-k)
\]
其中\(N\)是序列长度
序列圆周位移、相移
\[
x(n-l) \leftrightarrow X(k)e^{-j\frac{2\pi}{N}kl}\\
x(n)e^{j\frac{2\pi}{N}ln} \leftrightarrow X(k-l)
\]
插播一条DFS的性质:
周期卷积
两个周期都为\(N\)的周期序列,其卷积结果也是周期为\(N\)的序列
\[
\tilde{y} = \tilde{x}_1 \otimes \tilde{x}_2
\]
周期卷积定理
\[
\tilde{Y}(k) = \tilde{X}_1(k) \cdot \tilde{X_2}(k)
\]
对于非周期序列来说,可以用圆周位移来构造圆周卷积
圆周卷积
\[
y = x_1 \bigcirc x_2
\]
其中\(\bigcirc\)中应该有一个\(N\),但是这里打不出来,\(N\)是\(x_1,x_2\)序列长度;后面统一用\(\circledast\)代替
圆周卷积与DFT存在对应关系
\[
x_1 \circledast x_2 \leftrightarrow X_1(k)\cdot X_2(k)
\]
这个东西有什么用?
圆周卷积本身没有任何物理意义,但是由于其能被对应成DFT直乘,那么就存在一定用处
由于离散序列的卷积对应于DTFT的直乘,而\(X(\omega)\)是连续函数,这在计算机中是无法做到的
因此,若能有方法使得
\[
x_1(n) * x_2(n) = x_1(n) \circledast x_2(n)
\]
那么就有
\[
X_1(\omega) \cdot X_2(\omega) = X_1(k) \cdot X_2(k)
\]
这样计算机就能做了
帕斯瓦尔定理
\[
\sum_{n=0}^{N-1} x(n)y^*(n) = \frac{1}{N}\sum_{k=0}^{N-1}X(k)Y^*(k)
\]
7.5 基于DFT的LTI系统:如何让线性卷积等于圆周卷积
线性卷积
两个序列\(x(n),h(n)\),分别长\(L, M\),得到的输出\(y(n)\)
\[
y(n) = x(n) * h(n) =\sum_{k=1}^{L-1}x(k)h(n-k)
\]
\(y(n)\)的长度为\(N_1=L+M-1\)
圆周卷积
\(y(n)\)的长度为\(N_2=\max\{L,M\}\)(短的一方用0补齐)
因此,想要使用圆周卷积表示线性卷积,那么需要用\(N_2\geq N_1=L+M-1\)的DFT
例:\(h(n)=\{1(0),2,3\},x(n)=\{1(0),2,2,1\}\),使用DFT和iDFT,求\(y(n)\)
解:线性卷积的长度为6,因此需要使用6点的DFT,得到结果是\(y(n)=\{1(0),4,9,11,8,3\}\)
如果用4点DFT呢?得到的结果是\(y(n)=\{9,7,9,11\}\),产生这个结果的原因是\(8,3\)经过圆周到了\(1,4\)的位置
\(1+8=9, 4+3=7\)
利用圆周卷积计算线性卷积
步骤如下
- \(x(n)\)添加\(M-1\)个0,\(h(n)\)添加\(L-1\)个0,二者的长度都是\(L+M-1\)
- 利用\(L+M-1\)点的DFT计算\(Y(k)\),逆变换为\(y(n)\)
优点:在引入FFT后很快
缺点:必须等到所有的信号,延迟巨大
解决大延迟
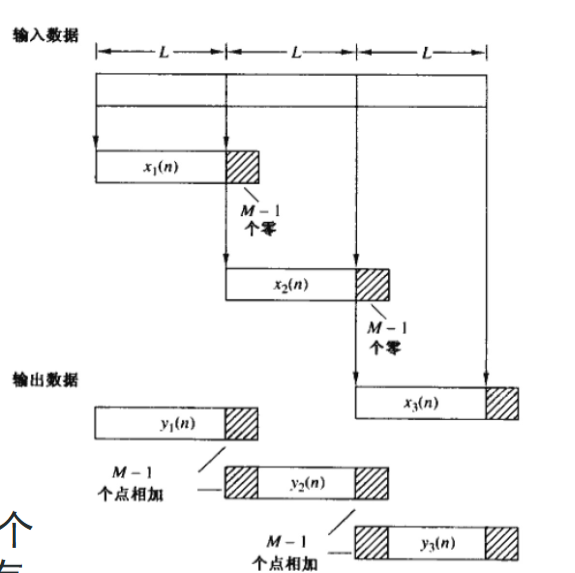
将信号分为小片段进行处理,步骤如下
- 将\(h(n)\)补到\(L+M-1\),将输入\(x(n)\)划分为长度为\(L\)的小段,这个\(L\)相比于整个序列很小
- 对输入的\(x_i(n)\)补\(M-1\)个0,计算\(X_i(k)\cdot H(k)\)
- 得到\(y_i(n)\),注意\(y_i(n)\)之间存在重叠部分,将重叠部分相加,得到\(y(n)\)