6 数字LTI系统的频域分析
6.1 LTI系统的特性
输出信号\(y(n)\)可以表达为输入信号\(x(n)\)和单位冲激响应\(h(n)\)的卷积
\[
y(n) = h(n)*x(n)
\]
当\(x(n) = A e^{j\omega_0 n}\)时,特别的\(y(n)=H(\omega)Ae^{j\omega n}\),证明如下
\[
\begin{align}
y(n) &= h(n)*x(n)=\sum_{k=-\infty}^\infty h(k)\cdot x(n-k)\\
&=\sum_{k} h(k)e^{-j\omega_0 k}\cdot e^{j\omega n}\\
&=H(\omega_0)x(n)
\end{align}
\]
称\(e^{j\omega_0 n}\)为系统的特征函数,\(H(\omega_0)\)为系统的特征值
\(H(\omega)\)的特性
\[
H(\omega) = \sum_k h(k)\cos(\omega k)+jh(k)\sin{\omega k}
\]
对于实系统,\(h(n)\)为实数,那么有\(H(\omega) = H_R(\omega)+jH_I(\omega)\),其中
\[
|H(\omega)| = \sqrt{H_R^2+H_I^2}\\
\angle H = \tan^{-1}\frac{H_I}{H_R}
\]
不难看出\(|H|\)是偶函数,\(\angle H\)是奇函数,\(H(\omega)\)有共轭对称性
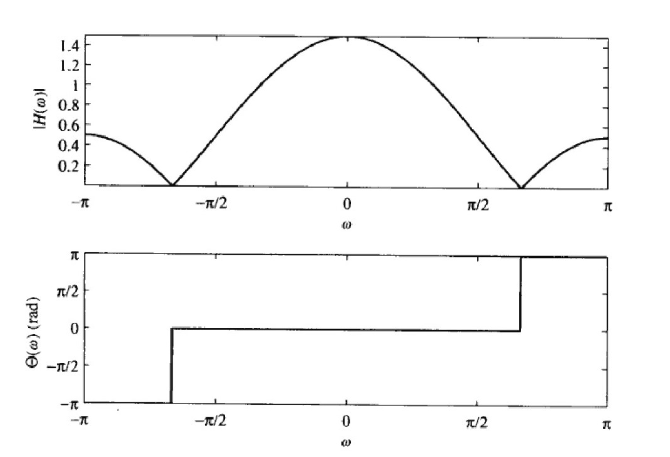
滑动平均Filter
一个3点滑动Filter可以表示为
\[
y(n) = \frac{1}{3}[x(n-1)+x(n)+x(n+1)]
\]
那么\(H(\omega)=\frac{1}{3}(1+2\cos(\omega)),|H|=|H(\omega)|\)(这里是绝对值),\(\angle H = \angle(1+2\cos(\omega))\)(注意正负)
图像如下
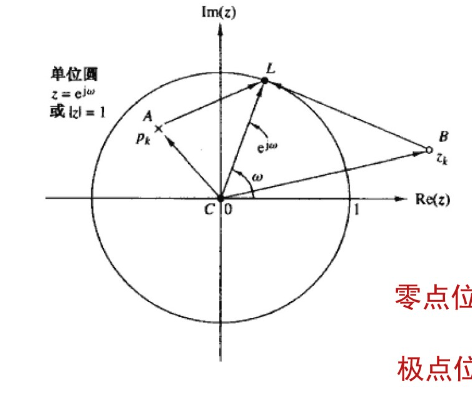
6.2 有理分式系统的响应
当一个系统函数可以表达为
\[
H(\omega)=b_0e^{j\omega k}\frac{\Pi (e^{j\omega}-z_i)}{\Pi(e^{j\omega}-p_i)}
\]
时,可以使用0极点图对\(|H|,\angle H\)进行估计,从而大致判断通频带
注意DTFT是\(r=1\)的特殊的Z变换,故实验点应该在单位圆上,如下图
进行估计时只需要将角度\(\omega\)从0°转到\(\pi\)就行,根据共轭对称性得到另一边
6.3 作为频率选择滤波器的LTI系统
\[ y=h*x\\ |Y| = |H||X|\\ \angle Y=\angle H+\angle X \]
\(|Y|\)与通频带有关
一个滤波器的通频带可以通过0极点图进行估计,大致而言存在以下关系
- 极点越靠近低频点的单位圆,通频带越低
- 将低通滤波器的0极点关于虚轴对称,可以得到高通滤波器
\(\angle Y\)与滤波器相位有关
信号经过滤波器时相位也会有影响,当然不希望相位被打乱
为了得到有序信号,即\(y(n)=Ax(n-k)\),滤波器应当是\(|H|e^{-j\omega k}\),相位是\(-\omega k\),是线性相位(存在截距也行)
称相位的负倒数\(\tau({\omega})=-\frac{d\Theta}{\omega}=k\)时群时延,是常数
群时延是常数的滤波器才是可以使用的
例:\(h(n)=\begin{cases}1,0\leq n\leq N\\0,\, \,\,\,o.w.\end{cases}\)是线性相位吗
解:\(H(\omega) = \frac{1-e^{-j\omega(N+1)}}{1-e^{-j\omega}}\),\(\angle H = \angle (1-e^{-j\omega(N+1)})-\angle(1-e^{-j\omega})\)
\[
\angle 1-e^{-j\omega} = \tan^{-1}\frac{\sin\omega}{1-\cos\omega}
\]
使用\(2\sin^2\omega/2 = 1-\cos\omega\),化简得到上式右边等于\(\tan^{-1}(\tan(\frac{\pi}{2}-\frac{\omega}{2}))=\frac{\pi-\omega}{2}\),同理处理前者,最终得到
\[
\angle H = -\frac{N}{2}\omega
\]
是线性相位
常见的具有线性响应的滤波器
只有\(h(n)\)满足下面的情况时,FIR滤波器才具有线性相位
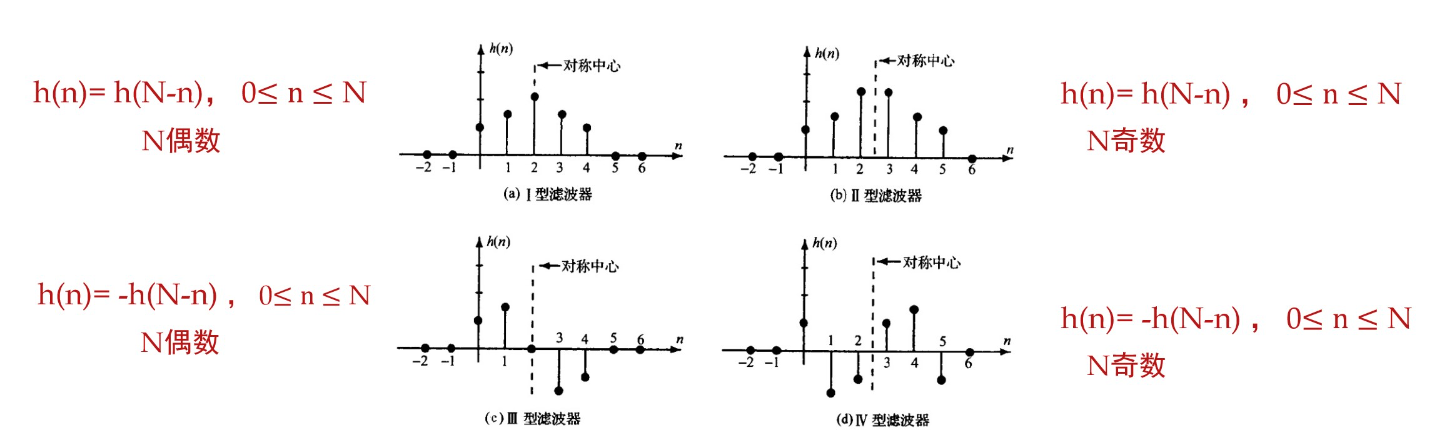
下面求每个滤波器的群时延

结论,每个滤波器的群时延都是\(\tau(\omega)=\frac{N}{2}\)
6.4 LTI系统的可逆性
系统可逆的充要条件:输出\(y\)与输入\(x\)一一对应
那么有
\[
x(n) = h_1(n)*h(n)*x(n)
\]
其中\(h_1(n)\)是逆系统,那么
\[
h_1*h=\delta\\
H_1H=1\Rightarrow H_1=H^{-1}
\]
求逆系统是要注意收敛域的选取和多值性,如
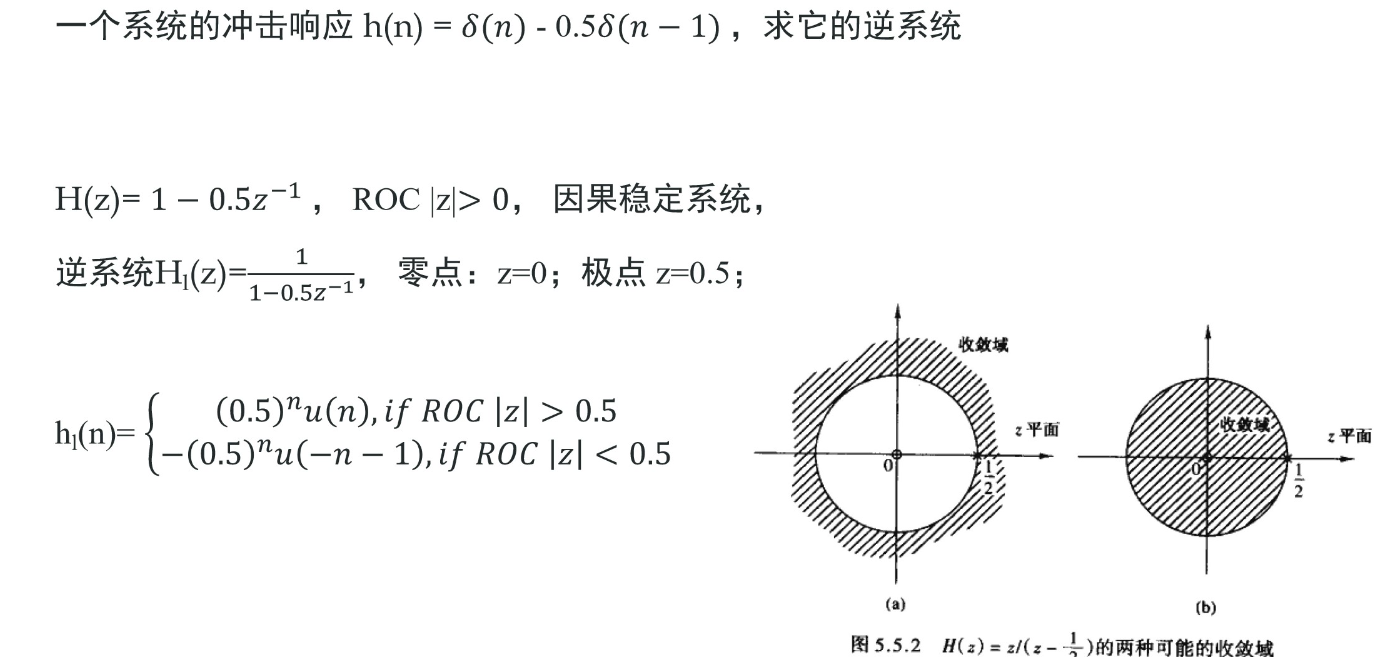
6.5 全通系统
对任意频率的信号,全通,即
\[
|H| = 1
\]
为了保证常数群时延,\(H = e^{-jk\omega}, H(z)=z^{-k}\)
全通系统可以作为相位补偿使用
6.6 低通高通转换
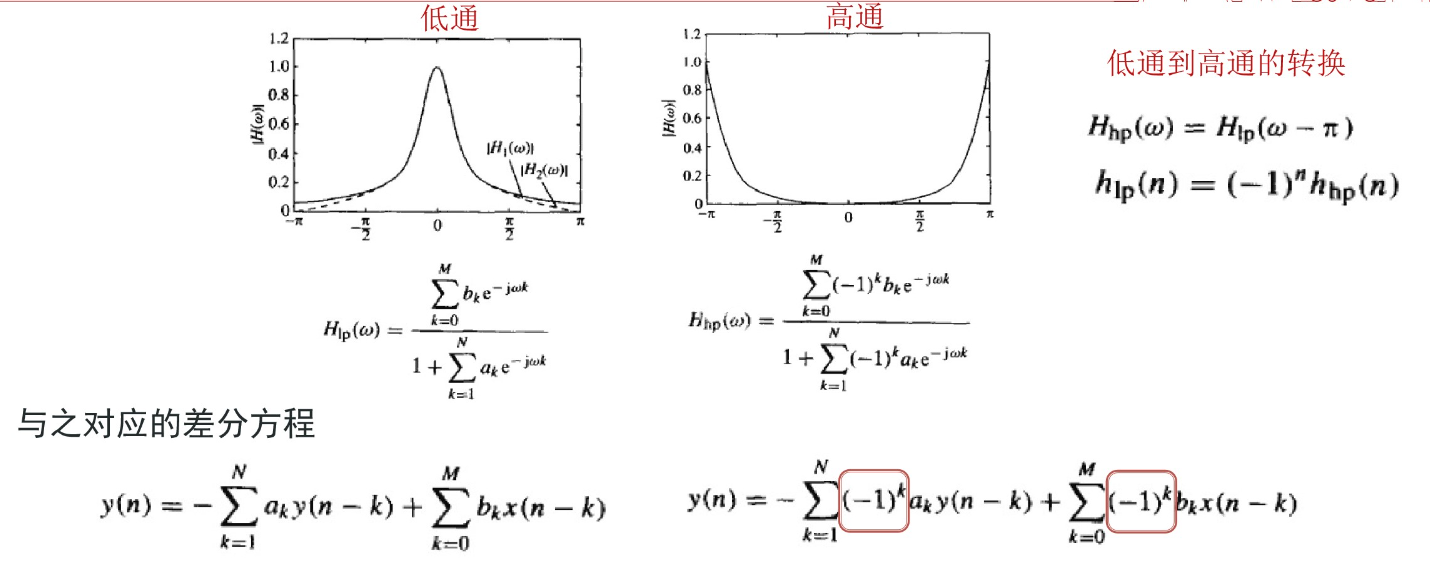
也就是用\(\pi-\omega\)代换\(\omega\)