5 数字信号的频域分析
5.1 连续周期信号的傅里叶级数
信号\(x(t)=x(t+T)\),基波频率\(\Omega_0 = \frac{2\pi}{T}\),谐波频率\(\Omega_k = \frac{2\pi k}{T},k\in\Z\)
可以将信号分解为傅里叶级数,也可以由傅里叶级数合成原始信号
\[
x(t) = \sum\limits_{k=-\infty}^\infty C_k e^{j\frac{2\pi}{T}kt }\\
C_k = \frac{1}{T}\int_T x(t) e^{-j\frac{2\pi}{T}kt}dt
\]
存在帕萨瓦关系,平均功率\(P_x\)和功率谱密度\(|C_k|^2\)的关系为
\[
P_x = \frac{1}{T}\int_T|x(t)|^2dt = \sum\limits_{k=-\infty}^\infty |C_k|^2
\]
5.2 连续非周期时间信号的傅里叶变换
将周期拉为无限长,得到傅里叶变换
\[
x(t) = \frac{1}{2\pi}\int_\infty X(j\omega)e^{j\omega t}d\omega\\
X(j\omega) = \int_\infty x(t)e^{-j\omega t}dt
\]
能量谱密度为\(S_{xx}(\omega) = |X(\omega)|^2\)
帕萨瓦关系为
\[
E_x = \int|x(t)|^2dt = \frac{1}{2\pi}\int|X(j\omega)|^2d\omega
\]
5.3 离散周期时间信号的傅里叶级数(DTFS)
离散信号\(x(n)\)满足\(x(n) = x(n+N)\),基波频率\(\Omega_s = \frac{2\pi}{N}\),谐波频率\(\Omega_k = \frac{2\pi k}{N},k\in\Z\)
同样可以分解为傅里叶级数
\[
x(n) = \sum\limits_{k=0}^{N-1}C_k e^{j\frac{2\pi}{N}kn}\\
C_k = \frac{1}{N} \sum\limits_{n=0}^{N-1}x(n) e^{-j\frac{2\pi}{N}kn}
\]
功率谱密度为\(|C_k|^2\)
帕萨瓦关系为
\[
P_x = \sum\limits_{k=0}^{N-1}|C_k|^2 = \frac{1}{N}\sum\limits_{n=0}^{N-1}|x(n)|^2
\]
\(C_k\)往往是一个复数,其相位谱的含义就是这个频率的分量的时延
5.4 离散非周期时间信号的傅里叶变换(DTFT)
将周期拉为无限长,得到傅里叶变换
\[
x(n) = \frac{1}{2\pi}\int _{-\pi}^{\pi} X(\omega)e^{j\omega n }d\omega\\
X(\omega) = \sum\limits_{n=-\infty}^\infty x(n)e^{-j\omega n}
\]
观察下面的式子(DTFT),不难发现\(X(\omega) = X(\omega + 2\pi)\),故实际操作中只看一个周期\([-\pi,\pi]\)的频谱
在时域上\(x(n)\)非周期,得到的\(X(\omega)\)是连续函数,有对应的相位谱和幅度谱,相位谱的值域为\([-\pi,\pi]\)
能量谱密度为\(S_{xx}(\omega) = |X(\omega)|^2\)
帕萨瓦关系为
\[
E_x = \sum\limits_{n=-\infty}^\infty|x(n)|^2 = \frac{1}{2\pi}\int_{-\pi}^{\pi}|X(\omega)|^2d\omega
\]
实际上,DTFT就是在\(r=1\)时的\(Z\)变换,上文已经证明
常用的DTFT变换对
指数序列
\(x(n) = a^nu(n),|a|<1\),带公式得到
\[
X(\omega) = \frac{1}{1-ae^{-j\omega}}
\]
这个信号的幅度谱为\(|X(\omega)| =\left| \frac{1}{1-a\cos\omega+ja\sin{\omega}} \right|=\frac{1}{\sqrt{(1-a\cos\omega)^2+(a\sin{\omega})^2}}=\frac{1}{\sqrt{1+a^2-2a\cos\omega}}\)
相位谱为\(\angle X(\omega) = -\tan^{-1}{\frac{a\sin{\omega}}{1-a\cos{\omega}}}\)
窗序列
定义窗序列为
\[
x(n) =
\begin{cases}
1\,\,\,\, -L\leq n\leq L\\
0\,\,\,\, o.w.
\end{cases}
\]
那么\(X(\omega)\)就是
\[
X(\omega) = \frac{\sin\left[(L+1/2)\omega\right]}{\sin{(\frac{1}{2} \omega)}}
\]
如果频域上是窗函数呢?
\[
x(n) = \frac{1}{2\pi}\int_{-\pi}^\pi X(\omega)e^{j\omega n}d\omega=
\begin{cases}
\frac{\sin(n\omega_c)}{\pi n}\,\,\,\,\, n\neq0\\
\frac{\omega_c}{\pi}\,\,\,\,\, n=0
\end{cases}
\]
其中\(\omega_c\)是奈奎斯特频率
注意需要将\(n=0\)的情况分开,因为\(n=0\)指数项消失了
吉布斯现象
就是窗函数边缘是振荡的,因为做不到时域无限长的信号,相当于将无限长的信号在时遇上乘一个窗函数
那么频域就是一个理想的窗函数卷积一个辛格函数,就造成了边缘的振荡
吉布斯现象就是在\(X(\omega)\)的不连续点处,\(X_N(\omega)\)逼近\(X(\omega)\)的振荡行为
DTFT的性质
- 线性,\(ax_1(n)+bx_2(n) \leftrightarrow aX_1(\omega)+bX_2(\omega)\)
- 时移特性,\(x(n-k)\leftrightarrow X(\omega)e^{-jk\omega}\)
- 频移特性,\(x(n)e^{j\omega_0n} \leftrightarrow X(\omega - \omega_0)\)
- 翻转特性,\(x(-n)\leftrightarrow X(-\omega)\)
- 时域微分,\(\frac{d}{dn}x(n) \leftrightarrow j\omega X(\omega)\)
- 频域微分,\(nx(n) \leftrightarrow j\frac{d}{d\omega}X(\omega)\)
- 卷积定理,\(x_1(n)*x_2(n) \leftrightarrow X_1(\omega)\cdot X_2(\omega)\)
- 窗口定理/调制定理,\(x_1(n)\cdot x_2(n) \leftrightarrow \frac{1}{2\pi}X_1(\omega)*X_2(\omega)\)
- 共轭对称,若\(x(n)\)为实信号,那么\(X(\omega) = X^*(-\omega)\),这个定理说明,在实信号的DTFT中,只需要变换一半的频谱
一些例子
对下面的信号做DTFT
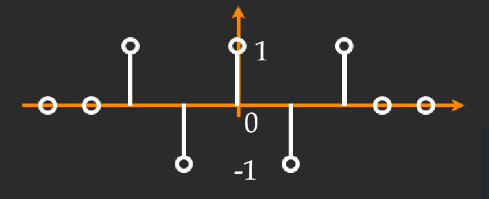
这是一个窗函数乘以相位因子,如果\(x(n)\)是窗函数,那么这个信号就是\(y(n) = e^{j\pi n}x(n)\),其DTFT就是\(X(\omega-\pi)\),就可以从低通滤波器变成高通
对下面的信号做iDTFT
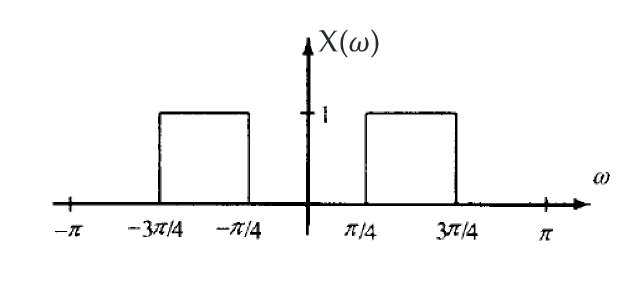
这是一个大窗减去小窗,是长度为\(3\pi/2\)的频域窗减去一个长度为\(\pi/2\)的频域窗,得到的时域信号也就是二者相减
\[
x(n) =
\begin{cases}
\frac{1}{\pi n }(\sin(\frac{3\pi}{4}n)-\sin(\frac{\pi}{4}n))\,\,\, n\neq 0\\
\frac{1}{2}\,\,\, n=0
\end{cases}
\]
例:已知\(X(\omega)\),求\(x(2n+1)\)的DTFT
解:常规做法是\(N=2n+1 \rightarrow x(N)\),但是\(x(2n+1)\)是一个奇数序列,那么在
\[
X_1(\omega) = \sum_{N} x(N)e^{-j\omega \frac{N}{2}}e^{j\frac{\omega}{2}}
\]
这里,\(N\)是一个奇数序列,换言之这个不是常规的DTFT,故不能这么做
观察到
\[
\hat{x} = \frac{1}{2}(x+(-1)^{n+1}x)=\frac{1}{2}(x-e^{jn\pi}x)
\]
利用DTFT的性质进行变换
但是观察到\(x(2n+1)\)是对序列\(\hat{x}(n)\)的平移加缩放,因此还需要进行变换
此时有\(X_1(\omega) = \sum\limits_{N}x(N)e^{-j\omega\frac{N}{2}}e^{j\omega/2}\),这里是奇数序列,可以用\(\hat{x}(n)\)代替,得到
\[
X_1(\omega) = e^{j\frac{\omega}{2}}\hat{X}(\frac{\omega}{2})
\]