4 系统的差分方程
4.1 LTI系统的系统函数
一个系统\(y(n) = x(n)* h(n)\),两边Z变换,得到
\[
Y(z)=X(z)\cdot H(z)
\]
其中\(H(z)\)就是系统函数,\(H(z)=\sum\limits_{n=-\infty}^\infty h(n)z^{-n}\),\(h(n)\)是单位冲激响应
系统稳定性
充要条件是\(\sum\limits_{n=-\infty}^\infty|h(n)|<\infty\),也就是\(|z|=1\)时\(H(z)\)收敛
因此当ROC包含\(|z|=1\)时系统稳定
其实就是系统在的傅里叶变换存在,即在s平面上包含虚轴
系统因果性
这里默认\(H(z)=\frac{Q(z)}{P(z)}\),那么充要条件就是ROC在最大极点之外
参考s平面上在最大极点的右边为ROC
那么一个因果系统的充要条件就是\(ROC = R_h <|z|\leq\infty,|R_h|<1\)
也就是所有的极点都在单位圆内
4.2 单边Z变换
定义单边z变换为
\[
X^+(z) = Z[x(n)u(n)]=\sum\limits_{n=0}^\infty x(n)z^{-n}
\]
其特点是
- 对因果信号来说无所谓单不单边
- ROC总在最大极点之外
位移性
假设\(k>0\),那么有
\[
Z^+[x(n-k)] = z^{-k}[X^+(z)+\sum\limits_{n=1}^kx(-n)z^n]\\
Z^+[x(n+k)] = z^{k}[X^+(z)-\sum\limits_{n=0}^{k-1}x(n)z^{-n}]
\]
4.3 常系数线性差分方程
形如
\[
\sum\limits_{i=0}^N a_iy(n-i) = \sum\limits_{j=0}^Mb_jx(n-j)
\]
若\(y(n)\)的初始状态为0,且\(x(n)\)是因果序列,那么两边z变换,得到
\[
\sum\limits_{i=0}^N a_iz^{-i}Y(z) = \sum\limits_{j=0}^Mb_jz^{-j}X(z)
\]
得到的系统函数一般是\(H(z) = \frac{Q(z)}{P(z)}\)
如果存在初始状态,那么就用单边Z变换
4.4 系统框图
直接I型系统结构
\[
Y(z) = \frac{b_0+b_1z^{-1}+b_2z^{-2}+\ldots + b_Mz^{-M}}{1+a_1z^{-1}+a_2z^{-2}\ldots + a_Nz^{-N}}\cdot X(z)
\]
那么结构为
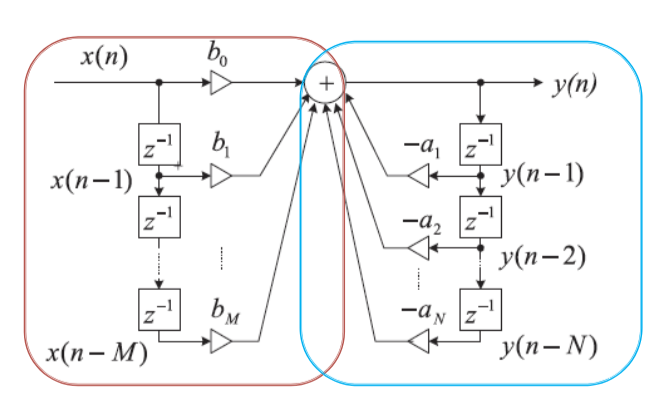
注意到这很直接,\(x(n-j)\)的系数都在左边,\(y(n-i)\)的系数的负数都在右边
直接II型系统结构
和SaS I中的直接型框图类似,方程同上,结果如下
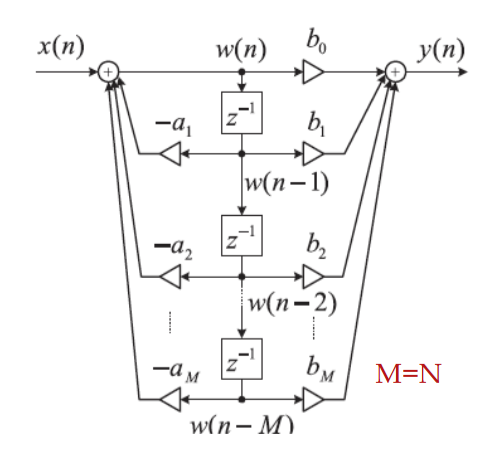
也就是分母是输入的负反馈,分子是输出
当然还有串联型和并联型框图,不赘述