2 信号采样与重建
与信号与系统1所讲一致,这里再操作一遍
整个流程
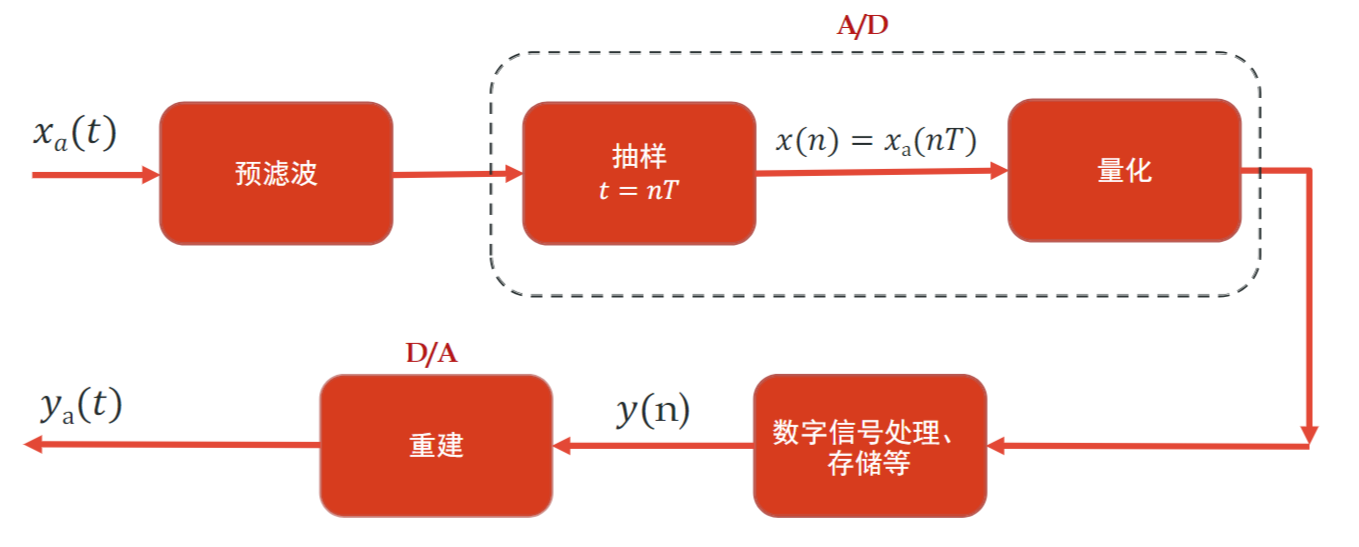
2.1 预滤波
不是必须的
当采样频率无法提升时,使用预滤波将原始信号\(\omega >\frac{\omega_s}{2}\)部分的信号过滤,防止混叠
\[
x(t)=x_a(t)*h_1(t)
\]
\[ X(j\Omega)=X_a(j\Omega)\cdot H_1(j\Omega) \]
其中\(H_1(\Omega)=\begin{cases}1 \,\,\,, |\Omega|\leq \Omega_s/2\\ 0\,\,\,, o.w.\end{cases}\)
2.2 抽样
这里讨论理想抽样模型,使用冲击串(非理想是阶跃串)
\(\hat{x}_a(t)=x_a(t)\cdot p_\delta(t)\),其中\(p_\delta(t)=\sum\limits_{k=-\infty}^{+\infty}\delta(t-kT)\)
为了方便积分变化,将采样函数级数展开,\(p_\delta(t)=\sum a_ke^{j\frac{2\pi}{T}kt},a_k=\frac{1}{T}\int_T{p_\delta(t)e^{-j\frac{2\pi}{T}kt}dt}=\frac{1}{T}\)
已知\(\mathcal{F}\{e^{j\Omega_s kt}\}=2\pi \delta(\Omega-k\Omega_s),\Omega_s=\frac{2\pi}{T},\delta(t-T)*x(t)=x(t-T)\)
故有
\[
\hat{X}_a(j\Omega)=\frac{1}{2\pi}X_a(j\Omega)*P_\delta(j\Omega)
\]
\[ P_\delta(j\Omega)=\frac{2\pi}{T}\sum\delta(\Omega-k\Omega_s) \]
得到
\[
\hat{X}_a(j\Omega)=\frac{1}{T}\sum{X_a(j\Omega-jk\Omega_s)}
\]
抽样得到的频谱是\(X_a(j\Omega)\)以\(\Omega_s\)为周期的延拓,幅度变为1/T
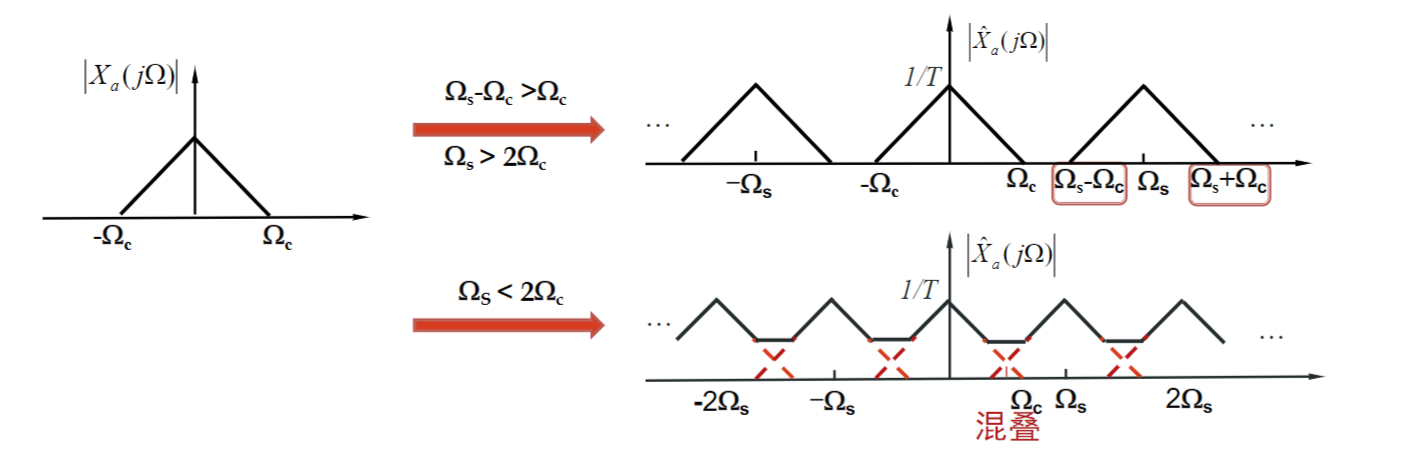
其中\(\Omega_c\)是原始信号的奈奎斯特频率,当\(\Omega_s-\Omega_c>\Omega_c\Rightarrow\Omega_s>2\Omega_c\)时,才不会产生混叠,此时唯一重建信号
实际上可以不可以等于,但一般没问题
定义信号的折叠频率为\(\Omega_s/2\),也就是预滤波的上限频率
2.3 重建
首先需要取出一个周期的频谱,很显然用幅值为T的低通滤波器\(H_r(j\Omega)=\begin{cases}T\,\,\,,|\Omega|\leq\Omega_s/2\\0\, \,\,\,,o.w.\end{cases}\)
这个滤波器对应的时域函数为\(h_r(t)=\frac{T}{\pi t}\sin(\frac{\pi t}{T})=\mathsf{sinc}(\frac{t}{T})\),其中\(\mathsf{sinc}(x)=\frac{\sin(\pi x)}{\pi x}\)
这在实际上是做不到的,我们无法得到一个无限长的信号
所以这是理想重建,有
\[
\begin{align}
x_r(t)=\hat{x}_a(t)*h_r(t) &=\left(x_a(t)\cdot p_\delta(t)\right)*h_r(t) \\
&=\left(\sum x_a(kT)\delta(t-kT)\right)*h_r(t)\\
&=\sum x_a(kT)h_r(t-kT)
\end{align}
\]
故重建信号就是由采样点为中心的sinc函数的加权和,这是由采样点内插得到的结果
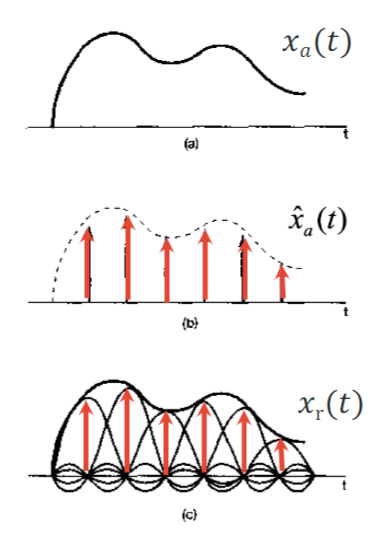
上图就是采样和重建的过程在图像上的显示
c的过程相当于对一个离散信号的频谱(有限),在最高频率之外加0值,不改变频谱图像,但是原图像对于新的图像来说就是一个加窗,也就是用低通滤波器重建
2.4 关于奈奎斯特率的几个结论
对于信号\(x(t), y(t)\),其奈奎斯特频率分别是\(f_x,f_y\),那么下面几个信号的奈奎斯特率分别是
- \(x(at)\Leftrightarrow \frac{1}{|a|}X(\frac{\omega}{a})\),为\(2|a|f_x\)
- \(x(t)+y(t)\),为\(2\max\{f_x,f_y\}\)
- \(x(t)* y(t) \Leftrightarrow X(\omega)Y(\omega)\),为\(2\min\{f_x,f_y\}\)
- \(x(t)\cdot y(t)\Leftrightarrow \frac{1}{2\pi} X(\omega)*Y(\omega)\),为\(2(f_x+f_y)\)