1 离散时间信号与系统
1.1 常见的典型序列
单位采样序列
\[
\delta (n)=\begin{cases}
1,\,\, n=0\\
0,\,\, o.w.\\
\end{cases}
\]
单位阶跃序列
\[
u(n)=\begin{cases}
1,\,\, n\geq 0\\
0,\,\, n<0\\
\end{cases}
\]
注意\(u(0)=1\)
\(u(n)=\sum\limits_{k=0}^\infty \delta(n-k)\),\(\delta (n)=u(n)-u(n-1)\)
矩形序列
\[
R_N(n)=\begin{cases}
1,\,\, 0\leq n\leq N-1\\
0,\,\, o.w.\\
\end{cases}
\]
N为矩形序列的长度,\(R_N(n)=u(n)-u(n-N)\)
实指数序列
\[
x(n)=a^nu(n)
\]
|a|<1,|x(n)|递减,x(n)收敛
正弦序列
\[
x(n)=\sin(\omega n)
\]
\(\omega\)是序列的数字域频率,单位rad
若正弦序列由模拟信号\(x_a(t)=\sin(\Omega t)\)采样得到,则\(x_a(nT)=\sin(\Omega nT)=x(n)=\sin(\omega n)\)
得到\(\omega =\Omega T\),其中Ω是模拟角频率,T是采样周期
复指数序列
\[
x(n)=e^{(\sigma+j\omega_0)n}
\]
我估计用不到
1.2 离散时间信号常见的特征、描述参数
信号能量
\[
E_x=\sum\limits_{i=0}^{n-1}|x(i)|^2
\]
信号功率
\[
P_X=\frac{1}{N}\sum\limits_{i=0}^{n-1}|x(i)|^2
\]
周期信号
存在最小正整数,使得\(x(n)=x(n+N)\)在\(n\in\N\)上成立
奇信号和偶信号
奇:\(x(n)=-x(-n)\);偶:\(x(n)=x(-n)\)
任意的信号\(x(n)\),其奇分量\(x_o=\frac{1}{2}[x(n)-x(-n)]\),偶分量\(x_e=\frac{1}{2}[x(n)+x(-n)]\)
共轭对称和共轭反对称
反对称:\(x(n)=-x^*(-n)\);对称:\(x(n)=x^*(-n)\)
任意的信号\(x(n)\),其反对称分量\(x_o=\frac{1}{2}[x(n)-x^*(-n)]\),对称分量\(x_e=\frac{1}{2}[x(n)+x^*(-n)]\)
1.3 离散时间信号基本运算
位移
\[
y(n)=x(n-n_0)
\]
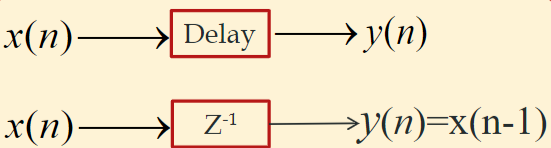
翻转
\[
y(n)=x(-n)
\]
加法
\[
y(n)=x_1(n)+x_2(n)
\]
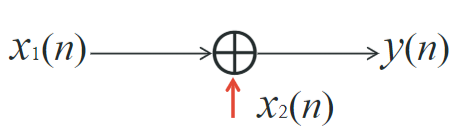
乘法
\[
y(n)=x_1(n)\cdot x_2(n)
\]
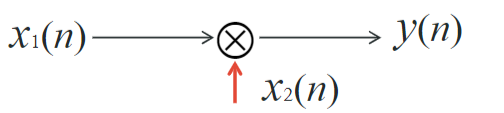
缩放
\[
y(n)=c\cdot x(n)
\]
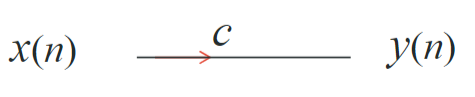
抽样
分为抽取(下采样)和插值(上采样)
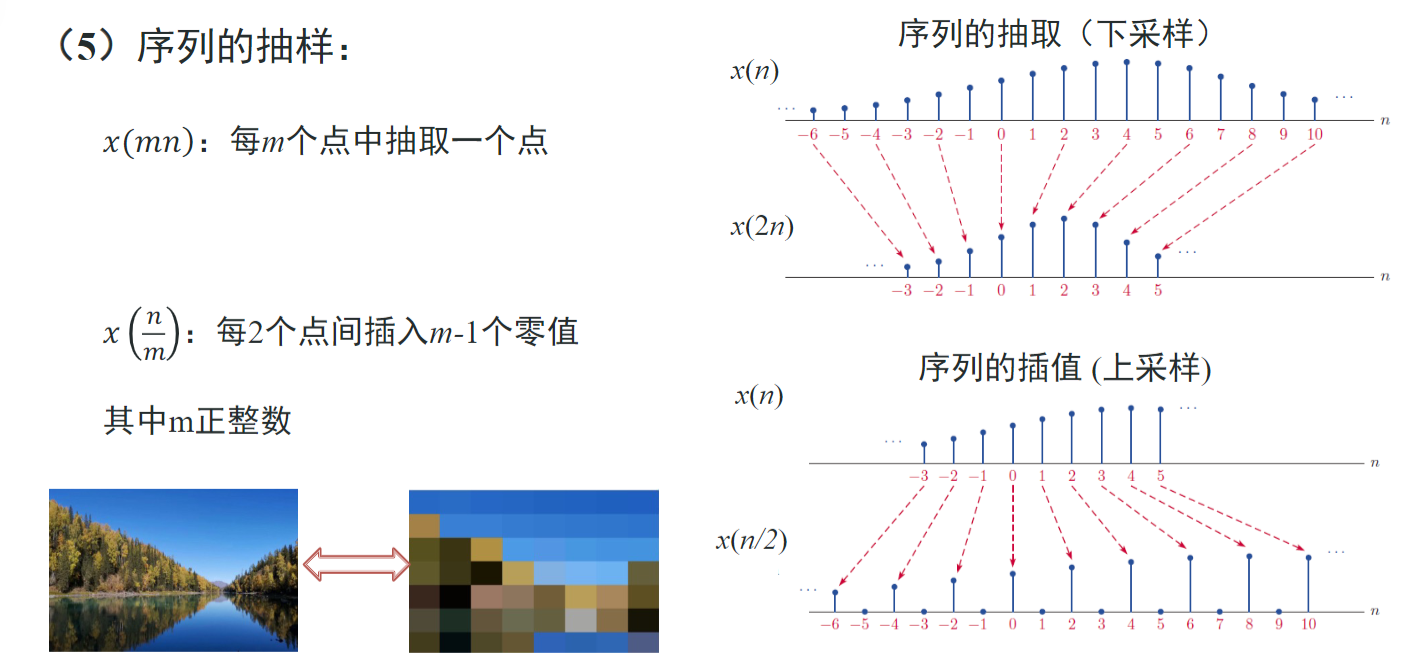
插值一般插0或均值
1.4 离散系统
将输入转换为输出的一种运算,\(y(n)=T[x(n)]\),其中\(T[]\)是离散系统
例:已知输入输出关系\(y(n)=0.25y(n-1)+0.5[x(n)+x(n-1)]\),画出系统的离散时间结构图
解:
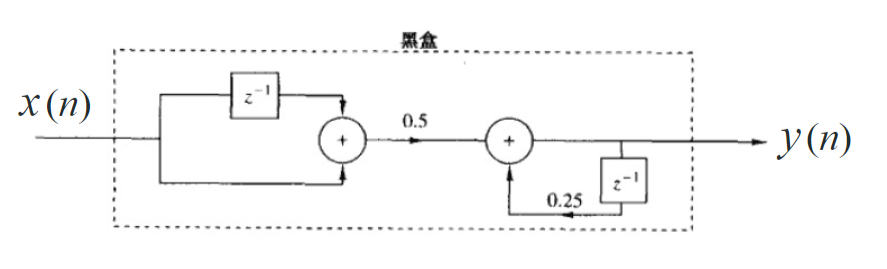
1.5 离散时间系统分类
静态系统(无记忆)与动态系统(记忆)
输出只取决于此刻的输入,为无记忆系统
时变系统与时不变系统
同SaS1
例:判断\(y(n)=x(-n)\)是否时变
解:令\(x_1(n)=x(n-N)\),则\(y_1(n)=x_1(-n)=x_1(-n-N)\),\(x(n-N)\)的输出则是\(y(n-N)=x(N-n)\)
故时变
线性系统与非线性系统
同时满足叠加性和齐次性
\(y(n)=ax(n)+b\)是增量线性系统
因果系统与非因果系统
输出与之后的输入无关,为因果
形如\(y(n)=f[x(n),x(n-m),y(n-k)],k>0,m>0\)为因果系统
稳定系统与非稳定系统
对于有界输入,输出有界,则稳定
1.6 离散时间LTI系统分析
\(x(n)\)可以表示为所有时刻\(x(k)\)值的累加和,即\(x(n)=\sum\limits_{k=-\infty}^{+\infty}x(k)\delta(n-k)\)
又已知\(\delta(t)\rightarrow h(t)\),系统是LTI系统,得到\(\delta(n-k)\rightarrow h(n-k),\sum x(k)\delta (n-k)\rightarrow \sum x(k)h(n-k)=x(n)*h(n)\)
故\(y(n)=x(n)*h(n)\),该式称为离散卷积
离散卷积的过程
观察公式\(\sum x(k)h(n-k)\),得到以下四步
- 将\(h(k)\)反转,得到\(h(-k)\)
- 将\(h(-k)\)向右位移n,得到\(h(n-k)\)
- 将\(x(k)\)和\(h(n-k)\)对应值相乘
- 将所有k处的乘积相加,得到\(y(n)\)
若序列\(x(n)\)和\(h(n)\)分别长N、M,卷积和/线性卷积的序列长度为N+M-1
例:一个LTI系统,\(h(n)=\{1,2,2,-1\}\),输入\(x(n)=\{1,2,3,1\}\),求输出结果
解:首先反转\(h(n)\)(或\(x(n)\),都行)得到\(h(-n)=\{-1,2,2,1\}\)
然后从无穷远处向右移动\(h(-n)\),第一个结果是\(x(1)=1\)与\(h(4)=1\)相交
然后再移动直到分离,最终序列为\(y(n)=\{1,4,9,10,6,-1,-1\}\),个数符合4+4-1=7个
**注:**序列表示法用箭头表示0时刻的位置
卷积和表明,n时刻系统的输出,与之前的输入也有关
即某一时刻的输出是之前很多次输入乘以各自的衰减系数之后的叠加
卷积遵守的数学定律
交换律:\(x(n)*h(n)=h(n)*x(n)\)
结合律:\(x(n)*[h_1(n)*h_2(n)]=[x(n)*h_1(n)]*h_2(n)\)
分配律:\(x(n)*[h_1(n)+h_2(n)]=x(n)*h_1(n)+x(n)*h_2(n)\)
可以用框图证明
卷积用途
- 是数据变化更加平滑
- 提取图像或者数据的特征
1.7 LTI系统的因果性和稳定性
因果性
对于LTI系统,因果性与**\(h(n)=0,n<0\)互为充要条件**
利用卷积的展开形式证明:
\[
y(n)=\sum h(k)x(n-k)=\sum\limits_{k=0}^\infty h(k)x(n-k)+\sum\limits_{k=-\infty}^{-1}h(k)x(n-k)
\]
后一项为0
例:已知\(h(t)=a^nu(n)\),求阶跃响应
解:\(y(n)=\sum\limits_{k=-\infty}^{\infty}a^ku(k)u(n-k)=\sum\limits_{k=0}^na^k=\frac{a^{n+1}-1}{a-1}\)
等比数列求和公式:\(S_n=a_1\frac{1-q^n}{1-q}\)
稳定性
LTI系统,稳定与\(\sum\limits_{n=-\infty}^{+\infty}|h(n)|<\infty\)互为充要条件
利用有界性的定义证明
1.8 有限/无限冲击响应
有限(Finite Impulse Response,FIR)
即\(h(n)=0\),当\(n<0,n\geq M\)时,此时\(y(n)=\sum\limits_{k=0}^{M-1}h(k)x(n-k)\)
无限(IIR)
即\(h(n)\)的非零区间无限大,此时\(y(n)=\sum\limits_{k=-\infty}^{\infty}h(k)x(n-k)\)
1.9 差分方程描述的离散时间系统
N阶线性常系数差分方程,形如
\[
\sum\limits_{i=0}^Na_iy(n-i)=\sum\limits_{j=0}^Mb_jx(n-j)
\]
线性:\(y(n-i),x(n-j)\)只有一次幂,无交叉项
常系数
N阶:输出的阶次确定
方框图见1.3的位移运算