均值的比较 3(对方差分析 ANOVA)

学习笔记

作者: MingXiao 2024/07/12

4.3.1 从t检验到ANOVA检验

$P=1-(1-\alpha)^{\mathsf{C}^2_n\cdot m}$ 这是非常大的一个数，所以抛弃多重检验

4.3.2 ANOVA原理

假定分为k组，共N个对象，每组N/k个 ANOVA做F检验，其核心是SST=SSB+SSW(Total=Between+Within)，注意自由度，证明见下

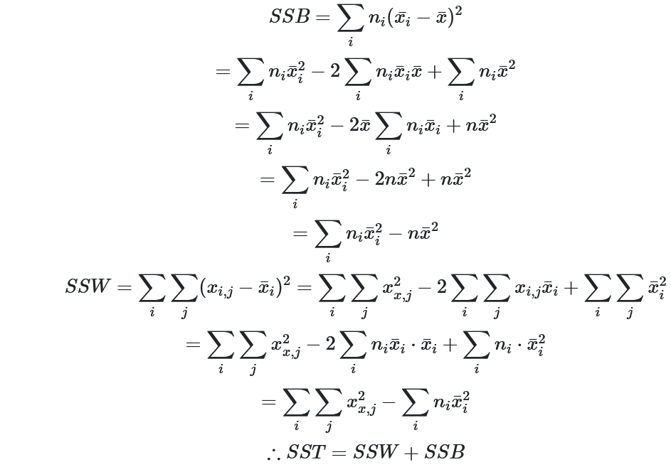得到ANOVA的报告表

Source	SS	df	MS	F	p-value	eta2
Total	SSB+SSW	N-1	/	MSB/MSW	F(k-1,N-k)对应的p	SSB/SST
Between	SSB	k-1	MSB	/	/	/
Within	SSW	N-K	MSW	/	/	/

$\mathsf{F}(df_B,df_W)=\frac{MSB}{MSW}=\frac{SSB/df_B}{SSW/df_W}$ $\eta^2=\frac{SSB}{SST}$ ，表示SST中有多少是SSB贡献的，也叫effect size

4.3.3 单因素对方差分析 1-Way ANOVA

类似于下面的分组，每组的受试样本都是不一样的，是1-Way ANOVA

Drug1	Drug2	Drug3
sub1,sub2,sub3	sub4,sub5,sub6	sub7,sub8,sub9

类似下面的，每组的受试样本一样的，是1-Way Repeated Measure ANOVA

Drug1	Drug2	Drug3
sub1,sub2,sub3	sub1,sub2,sub3	sub1,sub2,sub3

python代码click

import pingouin as pg
aov = pg.anova(data=data, dv="dependent variable", between="group", detailed=False, effsize=False)
dv表示选择对比的数据，因变量；between表示分组；detailed表示是否输出详细信息；effsize表示是否输出eta2
上面是1-way anova的
aov = pg.rm_anova(data=None, dv=None, within=None, subject=None, detailed=False)
within表示不同的分组，subject表示个体

1-way ANOVA, 1-way RM ANOVA条件

独立观测
独立样本（1-way），重复/配对样本（1-way RM）
正态分布
方差齐性（1-way），球性（1-way RM）
连续变量
组内随机采样
组间样本量平衡

4.3.4 两两配对比较

当通过1-way ANOVA拒绝零假设后，要想确定是哪几组之间的存在显著差异，就要使用Post Hoc多重检验（事后检验）（不使用多重t检验的原因同上）

python代码

pt = data.pairwise_tukey(dv="MoodGain", between="Grouop")
其中dv是因变量，between是分组，上面是1-way的
pt = data.pairwise_ttests(dv="Scores",within="Test",subject="Sub_id",padjust="bonf")
上面是1-way RM ANOVA，不重要

最后得到的结果是


xxxxxxxxxx
       A         B  mean(A)  mean(B)    diff      se       T      p-tukey   hedges  
0  anxifree  joyzepam   0.7167   1.4833 -0.7667  0.1759 -4.3596   0.0015   -2.3234
1  anxifree   placebo   0.7167   0.4500  0.2667  0.1759  1.5164   0.3117    0.8081
2  joyzepam   placebo   1.4833   0.4500  1.0333  0.1759  5.8760   0.0010    3.1315

其中，diff=mean(A)-mean(B)，se是枢轴量的standard error，T是枢轴量观测值，p-tukey是T对应的p值的修正值，hedges不管

4.3.5 2-way ANOVA

原理

Gender\DRug	A	B
male	sub1,sub2,sub3	sub4,sub5,sub6
female	sub7,sub8,sub9	sub10,sub11,sub12

当出现上面这种有两个变量时，使用2-way ANOVA，假设是

H01：Factor1不同水平的均值没有差异
H02：Factor2不同水平的均值没有差异
H03：Factor1不同水平的均值差异与Factor2无关，即不存在交互作用

python代码

aov=data.anova(dv='MoodGain', between=["Drug","Therapy"],detailed=True)
和1-way类似的，只是between中有多个变量

其报告表如下


xxxxxxxxxx
      Source        SS        DF    MS          F     p-unc       np2
0            Drug  3.453333   2  1.726667  31.714286  0.000016  0.840909
1         Therapy  0.467222   1  0.467222   8.581633  0.012617  0.416956
2  Drug * Therapy  0.271111   2  0.135556   2.489796  0.124602  0.293269
3        Residual  0.653333  12  0.054444        NaN       NaN       NaN

意义和1-way相同，但是算法不同

2-way ANOVA比两个独立的ANOVA具有更高的统计功效（statistic power）,即更容易检测出主效应（很小的p值）故即使不关心两个变量间的相互作用，也使用2-way ANOVA进行检验