2 数据可视化
作者:
MingXiao
2.1 一般建议
看变化趋势:lineplot
看分布特征:boxplot,scatterplot,直方图,pdf
看关系:回归线,scatterplot+回归线,热图
plt.subplot(2, 2)用于生成一个2\(\times\)2的画布,可以存放四张图
2.2 箱体图认读
箱体图认读:
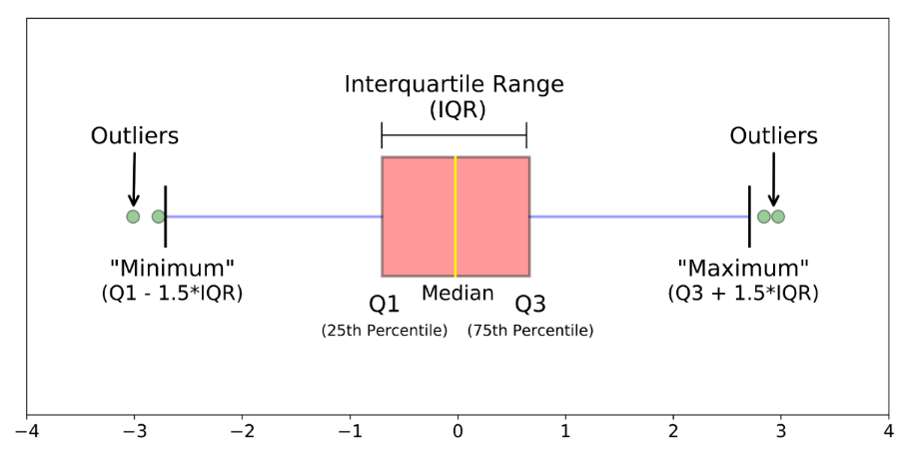
Q1,Median,Q3分别表示25,50,75分位点(非均值)
Minimum=Q1-1.5 * IQR,Maximum=Q3+1.5 * IQR
IQR=Q3-Q1(箱体长度)