预备知识

1.1 常用代码

click here

import pandas as pd
pd.read_csv("") #输入文件
pd.DataFrame.info() #该函数在调用时会显示以下信息：
#DataFrame 的形状（行数和列数）
#列名和各列的非空值数量
#列的数据类型
#内存使用情况
pd.DataFrame.describe() #它会计算以下统计信息：
#计数（count）：非空值数量
#平均值（mean）
#标准差（standard deviation）
#最小值（min）
#第25百分位数（25th percentile）
#中位数（50th percentile，即中位数）
#第75百分位数（75th percentile）
#最大值（max）
pd.DataFrame.groupby() #用于按照指定的列或多个列对数据进行分组
pd.DataFrame.agg() #同时计算多个值

1.2 生物医学数据类型

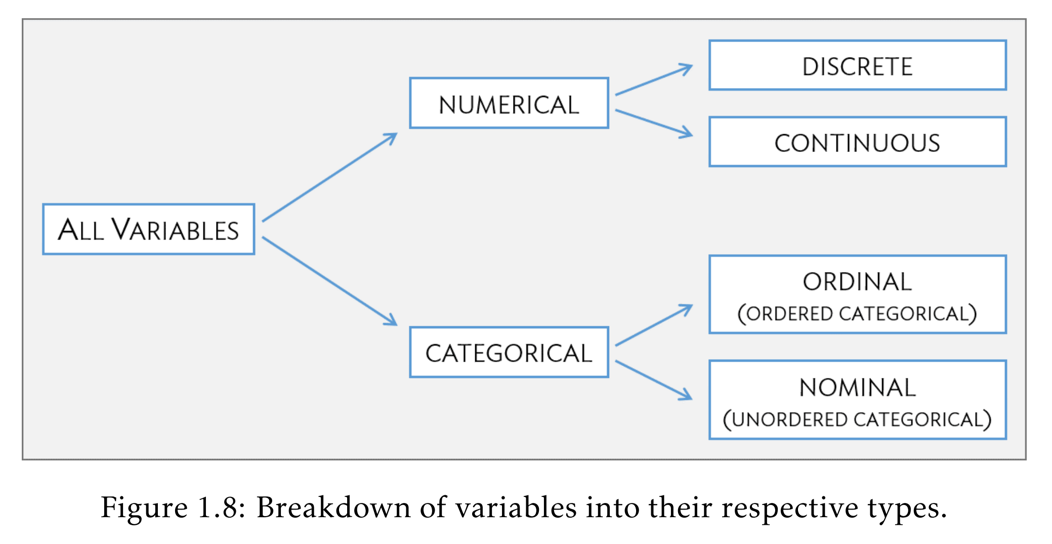
两个大类，四个小类：

可数的：
离散型：病毒感染人数，人的心率
连续性：人的血压值

可分类的：
有序(ordinal)：学生成绩（A/B/C/D）
无序(nominal)：病毒诊断结果（阳性/阴性）

1.3 常用术语

总体、样本、自变量、因变量、概率
样本的叫统计量，总体的叫参数

样本（Sample）和总体（Population）的例子：
对照组和实验组各10只卒中⼩⿏，研究某药物对卒中的⼲预作⽤，这个例⼦中有：
总体1：药物⼲预的任何卒中⼩⿏（⼤⼩不确定）
总体2：没有⽤药物⼲预的任何卒中⼩⿏（⼤⼩也不确定）
样本1：本实验中的药物⼲预组（n=10）
样本2：本实验中的对照组（n=10）
本实验有两个总体，两个样本

另一个例子：

1、总体有3个，分别是正常人群和两个服用不同药的人群；样本两个，分别100人
2、统计量：8h后两组血糖平均值；参数：总体数量，正常人SBP
3、样本大小
4、自变量是吃哪种药,因变量是8h后每个个体的血压

推断性统计：用样本来推测总体
描述性统计：用全体的数字特征来描述总体

1.4 大数定律和中心极限定理

注意，这与概统中的概念有所区别
大数定律(LLN) ：样本观测值越大，样本均值观测结果越接近总体均值
中心极限定理(CLT) ：样本均值的分布服从正态分布，该分布均值等于总体均值

用中心极限定理求均值click

data1= stats.norm.rvs(10,5,5000,random_state=100) #生成
data2= stats.norm.rvs(30,5,2000,random_state=100)
data=np.hstack((data1,data2)) #拼接数据 sample_means=[] #随机取数，求平均后存入数组
reps,ns=10000,50
for i in np.arange(10000):
sample_i=np.random.choice(data,ns,replace=True)
sample_means=np.append(sample_means,np.mean(sample_i)) #此时该数组的平均值就是总体平均值
print("总体均值是: %.2f " % np.mean(data))
print("样本均值分布的均值是: %.2f " % np.mean(sample_means))

1.5 常用分布和函数

正态分布：stats.norm()Z分布就是标准正态分布
T分布：stats.t()
二项分布：stats.binmo()
卡方分布：stats.chi2()

pdf:概率密度 stats.norm.pdf(x,\(\mu\),\(\sigma\))
pmf:概率质量 stats.binmo.pmf(k,n,p)
cdf:分布函数，用法同上
rvs:生成随机变量 stats.norm.rvs(size,\(\mu\),\(\sigma\))
ppf:下侧分位数 stats.norm.ppf(p,\(\mu\),\(\sigma\))
isf:上侧分位数 stats.norm.isf(p,\(\mu\),\(\sigma\))