7 控制系统的状态空间设计
7.1 控制器的极点配置
相比于根轨迹法只能确定主导极点,极点配置可以把所有的闭环极点配置到想要的位置
几个假设
- 系统完全可观测
- 如果系统状态完全可控,那么通过状态反馈增益矩阵就行
- 系统是单输入单输出
- 参考输入为0
7.1.1 状态反馈法
此方法要求系统完全可控
选取控制信号为
\[
u = -K_{1\times n}X_{n\times 1}
\]
即控制信号由瞬时状态决定,系统如下
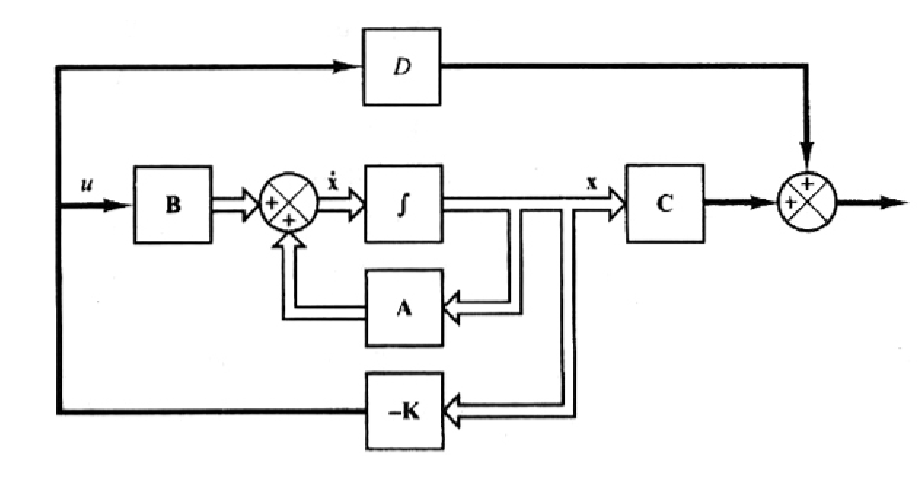
这个闭环系统没有输入量,参考输出也为0,最终的目的就是输出量为0
如果调节参考输入为常数,则这样的系统是调节器系统
如果会时变,则是控制系统
将控制信号带入状态空间方程,得到
\[
\dot{X}(t) = (A-BK)X(t)
\]
那么得到
\[
X(t) = e^{(A-BK)t}X(0)
\]
- 矩阵\(A-BK\)的特征值为调节器的极点
- 如果这些极点都在\(s\)平面的左半边,则当\(t\rightarrow\infty\)时,系统状态\(x_i=0\)
- 将调节器极点(也就是闭环极点)配置到所期望的位置,就是极点配置问题
7.1.2 任意配置极点
能够任意配置极点的充要条件是:系统状态完全可控
证明略,有两种方法配置\(K\)
变换矩阵T:一般用不到
检验系统的可控性,若不可控,那没得谈
根据\(|sI-A|=s^n+a_1s^{n-1}+\ldots+a_{n-1}s+a_n\)确定原始系统的闭环极点和\(a_i\)的值
求解变换矩阵\(T=M_{n\times n}W_{n\times n}\),其中
\[ M = [B, AB, \ldots,A^{n-1}B]_{n\times n}\\ W = \left[\begin{matrix} a_{n-1},a_{n-2},\ldots,a_1,1\\ a_{n-2},a_{n-3},\ldots,1,0\\ \ldots\\ a_1,\,\,\,1,\,\,\,\,\ldots\,\,\,\,\,\,,0\,\,\,\,\,,0\\ 1,\,\,\,\,0,\,\,\,\,\ldots\,\,\,,0\,\,\,\,0 \end{matrix}\right] \]利用期望的极点配置\(\Pi(s-p_i)=s^n+b_1s^{n-1}+\ldots+b_{n-1}s+b_n\)得到\(b_i\)的值
确定增益矩阵
\[ K = \left[ b_n-a_n,b_{n-1}-a_{n-1},\ldots,b_2-a_2,b_1-a_1\right]_{1\times n}T^{-1}_{n\times n} \]
值得一提,当原系统是可控标准型时,\(T=I_{n}\)
直接带入
对于低阶的系统有效
检验系统的可控性
假设增益矩阵是\(K=[k_1, k_2,k_3]_{1\times 3}\)
更改后的系统的闭环传递函数的特征方程应该是
\[ |sI-A+BK|=0 \]
其中\(BK_{n\times n}\)利用
\[ |sI-A+BK| =\Pi(s-p_i)=s^n+b_1s^{n-1}+\ldots+b_{n-1}s+b_n \]
来直接确定\(k_i\)的值
\(k_i\)越大,代表响应速度越大,所需要的能量也越大;实际系统中需要折衷考虑
7.2 状态观测器
思路和卡尔曼滤波一样
实际情况中不是所有的状态变量都可以用来反馈,需要用状态观测器估计(观测)不可用的状态变量
如果一个观测器能观测所有的状态变量,则称其为全阶状态观测器,对应于降阶和最小阶
能够设计状态观测器的充要条件是:系统满足可观测条件
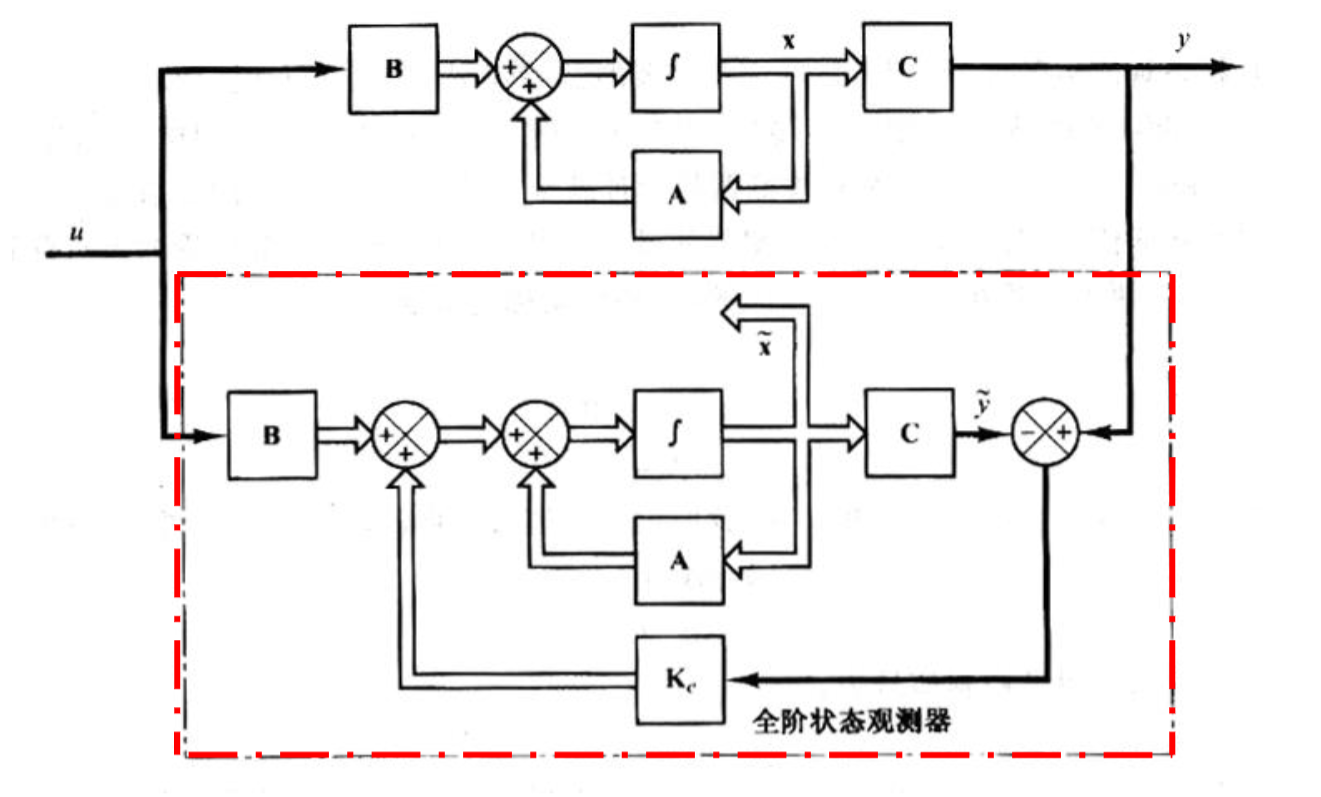
红框中的就是一个全阶状态观测器,基本思路如下
使用状态变量的观测/估计值\(\tilde{X}\)代替\(X\)进行计算,得到的状态空间为
\[ \dot{\tilde{X}} = A\tilde{X}+Bu+K_e(y-\tilde{y})\\ \tilde{y} = C\tilde{X} \]
其中\(K_{e\,\,{n\times 1}}\)是观测器的配置增益结合系统的状态方程,得到
\[ \dot{X}-\dot{\tilde{X}} = (A-K_eC)(X-\tilde{X}) \]令\(E=X-\tilde{X}\),那么
\[ \dot{E} = (A-K_eC)E \]\(E\)的解就是上面极点配置的问题,如果系统完全可观测,那么\(A-K_eC\)将具有任意的特征值,也就是极点
对这句话的解释:将\((A-K_eC)\)取转置,秩不变,得到\((A^T-C^TK_e^T)\),根据可观和可控的对偶性,这就是对偶系统的可控,那么就是本系统的可观
由于\(E\)是观测量和实际值的误差,当然希望\(E=0_{n\times 1}\),\(k_{ei}\)越大越好
但是一般而言,实际系统存在噪声,故这是一个抗干扰和快速响应的trade-off
配置方法同7.1.2,不赘述;是根据观测器的期望闭环极点配置的
7.3 控制器-观测器系统
7.3.1 控制和观测的独立性
一个完全可控和完全可观的系统,使用基于观测的状态变量进行极点配置,即
\[
u=-K_{1\times n}\tilde{X}
\]
那么
\[
\dot{X} = AX-BK\tilde{X} = (A-BK)X+BK(X-\tilde{X})=(A-BK)X+BKE\\
\dot{E} = (A-K_eC)E
\]
那么状态空间为
\[
\left[\begin{matrix}
\dot{X}\\
\dot{E}
\end{matrix}\right]
=
\left[\begin{matrix}
A-BK,\,\, BK\\
0,\,\,\,\,\,A-K_eC
\end{matrix}\right]
\left[\begin{matrix}
X\\
E
\end{matrix}\right]
\]
那么特征方程为
\[
\left|\begin{matrix}
sI-A+BK,\,\,\, -BK\\
0\,\,\,,\,\,\, sI-A+K_eC
\end{matrix}\right| = 0\Rightarrow|sI-A+BK|\cdot|sI-A+K_eC|=0
\]
根据行列式的性质,二者各自为0
也就是控制器和观测器是独立的,互不影响
7.3.2 控制器-观测器的传递函数
系统完全可测量,但是不能直接测量,即
\[
\dot{X} = AX+Bu\\
y=CX\\
u=- K\tilde{X}
\]
观测器方程为
\[
\dot{\tilde{X}} = (A-K_eC)\tilde{X}+Bu+K_ey\\
\Rightarrow \tilde{X} = (sI-A+K_eC+BK)^{-1}K_eY
\]
那么系统的闭环传递函数的倒数(自身不好表示,但是倒数好表示)就是
\[
\frac{U(s)}{Y{(s)}} = \frac{-K\tilde{X}}{Y(s)}=-K(sI-A+K_eC+BK)^{-1}K_e
\]
很显然这个要是串联那么设计起来会非常麻烦,故实际中一般都是并联的系统
7.4 最小阶观测器
如果\(y\)仅仅是\(m\)个状态变量的线性组合,那么余下的\(n-m\)个变量需要估计,需要一个\(n-m\)阶的降阶观测器
这个\(n-m\)的观测器就是最小阶观测器