6 控制系统的状态空间分析
6.1 传递函数的状态空间表达式
系统可以表达为
\[
y^{(n)} + a_1y^{(n-1)} + \ldots+ a_{n-1}y^{(1)} +a_ny = b_0u^{(n)} + b_1u^{(n-1)} +\ldots+b_{n-1}u^{'} +b_nu
\]
那么传递函数就是
\[
G = \frac{Y}{U} = \frac{b_0s^n+b_1s^{n-1}+\ldots+b_{n-1}s+b_n}{s^{n}+a_1s^{n-1}+\ldots+a_{n-1}s+a_n}
\]
注意上下是齐次的,否则需要添0
存在以下几个标准型
可控标准型
可控性:在有限时间内,系统输入无约束的\(u\),\(x(t_0)\)变化为\(x(t^{'}_0)\)
形如
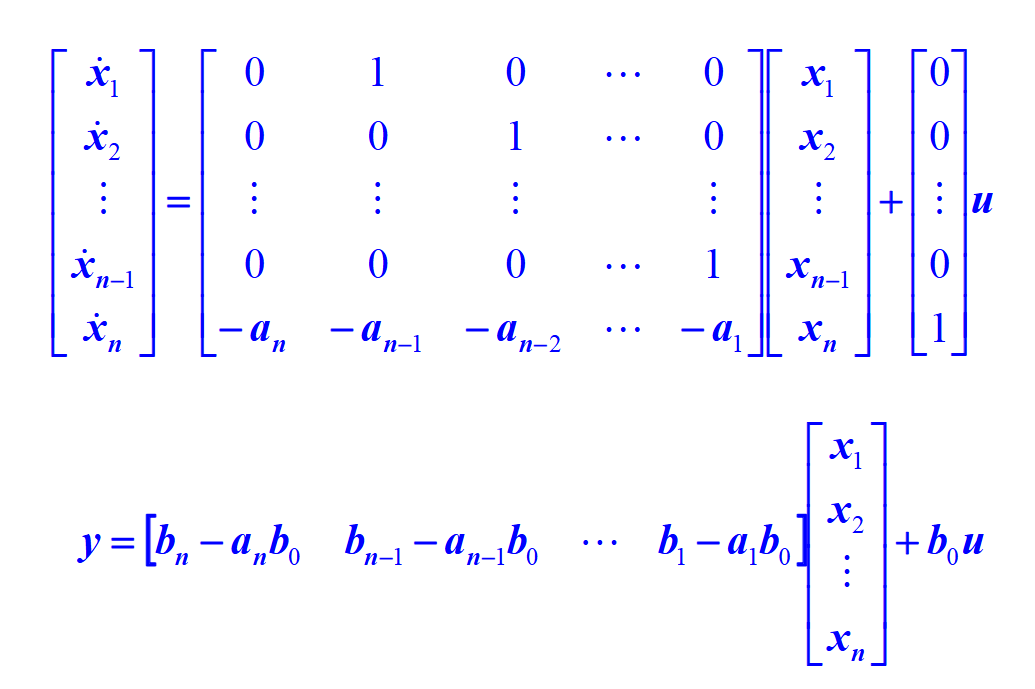
的状态空间方程,称为可控标准型
可观测标准型
可观测性:\(x(t_0)\)在有限时间内可由输出的观测值确定
形如

的状态空间方程,称为可观测标准型
不难发现,二者的系数矩阵存在以下关系
\[
A_2 = A_1^{T}\\
B_2 = C_1^{T}\\
C_2 = B_1^{T}\\
D_2 = D_1
\]
这个性质称为对偶性
对角线标准型
将传递函数化为
\[
G = b_0 + \sum\frac{c_i}{s+p_i}
\]
那么
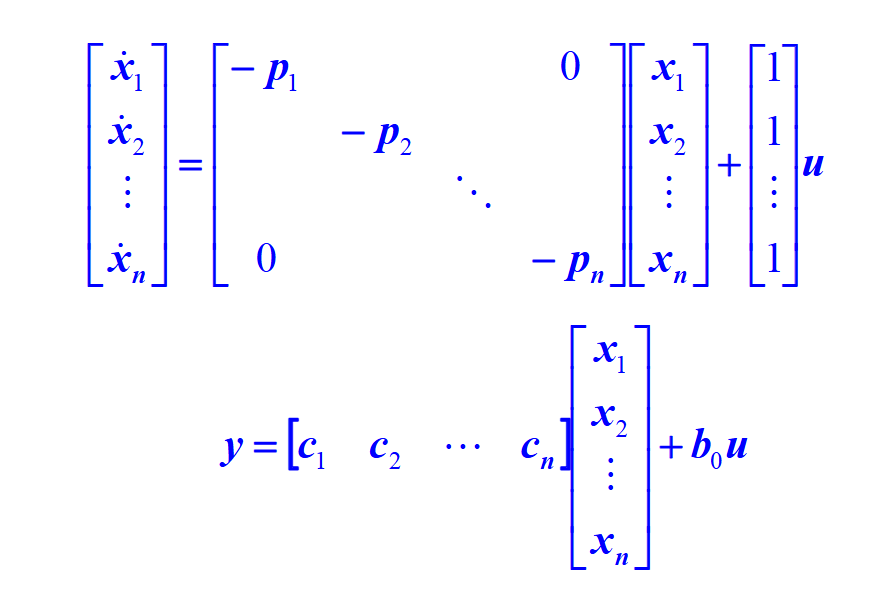
6.2 定常系统的状态空间方程的解
从本节开始,对符号做出区分:小写的字母一律为时域标量,如\(x\);大写的字母不带变量/带\(t\)一律为时域向量/矩阵,如\(A,X(t),X(0)\);大写字母带变量\(s\)的一律为Laplace变换,如\(X(s)\),至于是否为矩阵/向量,看上下文。
6.2.1 齐次方程
形如
\[
\dot{X} = A X
\]
的状态空间方程的解,不加证明的给出
\[
X = e^{At}X(0)
\]
其中\(X\)是列向量,\(A,e^{At}\)都是矩阵
解的过程使用了拉普拉斯变换
\[
(sI-A)X(s) = X(0)\Rightarrow X(s) = (sI-A)^{-1}X(0)
\]
不加证明给出
\[
\mathcal{L}^{-1}\{(sI-A)^{-1}\} = e^{At}
\]
\(e^{At}\)有以下的性质
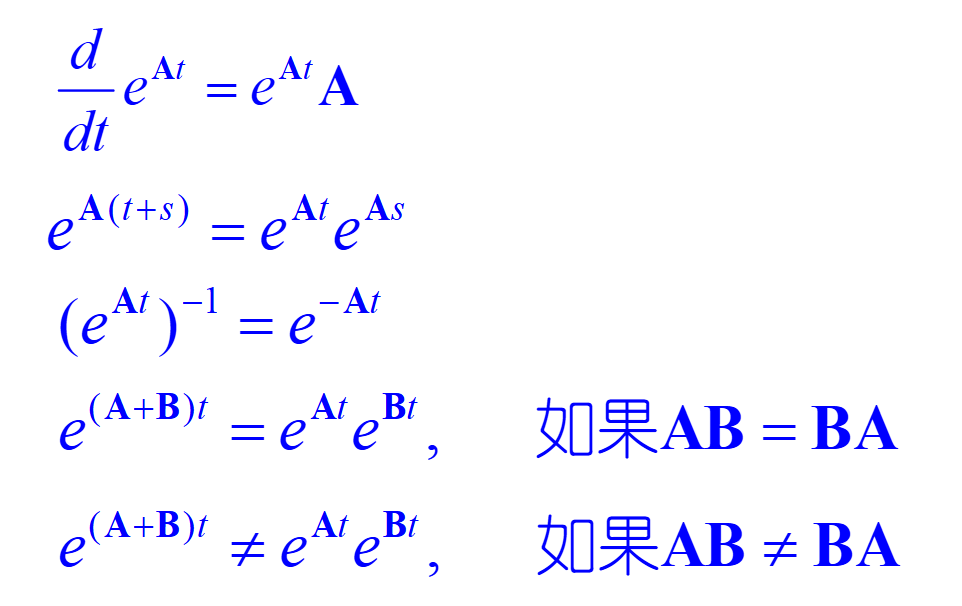
将系统的状态用初始值表达
\[
X = \Phi X(0)
\]
那么
\[
\Phi(t) = e^{At}
\]
称\(\Phi\)为系统的状态转移矩阵,包含系统自由运动的所有信息;方程的解仅仅是状态的转移
6.2.2 非齐次方程
形如
\[
\dot{X} = AX + BU
\]
做拉普拉斯变换
\[
(sI-A)X(s) = X(0)+BU(s)
\]
得到
\[
X(t) = e^{At}X(0)+e^{At}*BU(t)=\Phi(t)X(0)+\int^t_0\Phi(t-\tau)BU(\tau)d\tau
\]
若是在\(t_0\)时刻q起始,则
\[
X(t)=\Phi(t-t_0)X(t_0)+\int^t_{t_0}\Phi(t-\tau)BU(\tau)d\tau
\]
进一步打开卷积,不加证明的
\[
X(t) = e^{At}X(0)+A^{-1}(e^{At}-I)BU(t)
\]
6.3 可控性和可观测性
对于系统
\[
\dot{X}_{n\times 1} = A_{n\times n}X_{n\times1}+B_{n\times m}U_{m\times 1}\\
Y_{s\times 1} = C_{s\times n}X_{n\times 1}+D_{s\times m}U_{m\times 1}
\]
6.3.1 可控
如果在\(t_0\leq t\leq t_1\)内,施加一个无约束的控制信号,系统能从初始状态转移到任意终止状态,称系统在\(t=t_0\)可控;如果对于\(\forall t_0\),系统可控,称为系统为状态完全可控
状态完全可控的充要条件
先说结论:当且仅当向量组
\[
[B, AB, \ldots,A^{n-1}B]_{n\times nm}
\]
行满秩时,系统完全可控,该矩阵称为可控性矩阵
证明
设终止状态为\(X(t_1)=0\),对于任意的\(X(0)\)都能够达到这个状态,那么将其代入6.2.2节的方程中,得到
\[
X(0)=-\int^{t_1}_0e^{-At}BU(t)dt
\]
将\(e^{-At}\)展开为
\[
e^{-At} = \sum_{k=0}^{n-1}a_k(t)A^k
\]
那么
\[
X(0) = -\sum_{k=0}^{n-1}A^kB\int_0^{t_1}a_k(t)U(t)dt=-[B,AB,\ldots,A^{n-1}B][\int_0^{t_1}a_k(t)U(t)dt]^{T}
\]
那么为了能够表达所有的\(X(0)\),可控性矩阵必须满秩
输出完全可控的充要条件

这是直接截的图,放在本文档的语境下,这是一个\(s\times m(n+1)\)维矩阵,充要条件为其是行满秩
不可控制系统:包含一种物理上与输入量不相连接的子系统,存在部分状态变量不受控制
如果一个不可控制系统的不可控模块是稳定的,不稳定的模块是可控的,那么这个系统可稳定
利用A矩阵判断系统稳定性
计算A的特征值\(|sI-A|=0\),如果所有特征值的实部小于0,那么稳定
原因在于,\(|sI-A|=0\)就是闭环传递函数的特征方程
求出传递函数/矩阵,利用劳斯稳定判据
6.3.2 可观测
如果每一个状态\(x_i(t_0)\)都可以通过在有限时间\(t_0\leq t \leq t_1\)内由输出量\(y(t)\)的观测值确定,称系统为完全可观测
很显然当每一个状态分量\(x_i\)都影响输出\(Y_{s\times 1}\)时,系统完全可观测
状态完全可观的充要条件
先说结论:当且仅当向量组
\[
\left[\begin{matrix}
C\\
CA\\
\ldots\\
CA^{n-1}
\end{matrix}\right]_{sn\times n}
\]
列满秩时,系统完全可观,该矩阵的转置称为可观测矩阵
证明
忽略输入,仅看状态变量
\[
Y = CX = Ce^{At}X(0) = \sum_{k=0}^{n-1}a_kCA^kX(0)=[a_kX(0)]\left[\begin{matrix}
C\\
CA\\
\ldots\\
CA^{n-1}
\end{matrix}\right]
\]
为了满足每个状态变量都有独立的影响,可观测矩阵必须列满秩
可检测性
对于一个局部可观测系统,如果其不可观测的状态是稳定的,其可观测的状态是不稳定的,那么这个系统可检测
可检测与可稳定互为对偶