5 频率响应分析
5.1 频率响应
定义正弦传递函数,其实就是单位冲激响应的傅里叶变换\(G(j\omega)\),同样地定义相位和幅度
对于正弦信号\(x(t)=X\sin\omega t\),假定传递函数是多项式分式\(G(s)=\frac{P(s)}{Q(s)}\),那么
\[
Y(s) = G(s)\frac{X\omega}{s^2+\omega^2} = \frac{a}{s+j\omega}+\frac{\bar{a}}{s-j\omega}+\sum\frac{b_i}{s-s_i}
\]
其中\(a=\lim\limits_{s\rightarrow -j\omega}G(s)\frac{X\omega}{s-j\omega}=-\frac{XG(-j\omega)}{2j}\)是常数,为什么是\(a,\bar{a}\)经过通分可知,很显然,
\[
y(t) = ae^{-j\omega t}+\bar{a}e^{j\omega t}+b_ie^{s_it}
\]
对于一个稳定的系统,\(s_i\)的实部都在负半轴,故
\[
y_{ss}(t)=ae^{-j\omega t}+\bar{a}e^{j\omega t}=X|G(j\omega)|\sin(\omega t+\phi)
\]
上式的推导用到了\(G(j\omega)\)的共轭对称性,即\(|G(j\omega)|=|G(-j\omega)|,\phi_+=-\phi_-=\angle G(j\omega)\),其中\(\phi\)是相位(实际系统的时域响应一定是实函数,那么就有共轭对称性)
那么正弦响应就可以直接这么求
5.2 波特图
略,学了三次了也该会了
5.2.1 二阶因子
这是特别的,单独讲一下
对于一个标准的二阶因子,形如
\[
\frac{1}{1+2\zeta \left(\frac{j\omega}{\omega_n}\right)+\left( \frac{j\omega}{\omega_n} \right)^2}
\]
若\(\zeta>1\),那么可以化成两个一阶因子
若\(0<\zeta<1\),那么有新的方法简便计算(实际上是化成共轭复数作为一节因子的方法不再正确)
当\(\zeta\)较小时,转角频率处的响应与\(\zeta\)有关
频率响应曲线
不难发现
\[
20\lg|H| = -20\lg{\sqrt{\left( 1-\frac{\omega^2}{\omega^2_n}\right)^2+\left( \frac{2\zeta\omega}{\omega_n} \right)^2}}
\]
当\(\omega<<\omega_n\)时,\(20\lg|H| = -20\lg{1}=0\mathsf{dB}\)
当\(\omega>>\omega_n\)时,\(20\lg{|H|} = -40\lg{\frac{\omega}{\omega_n}}\)
在\(\omega_n\)处,根据\(\zeta\)的不同有如下
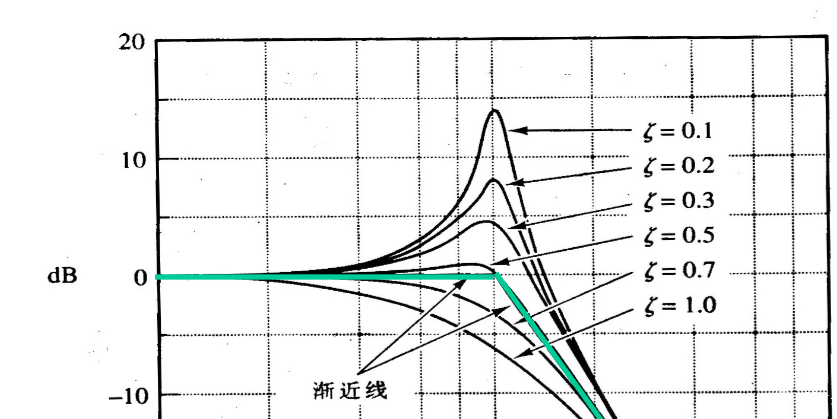
实际上就是系统在\(\omega_n\)附近存在共振频率,计算得到
\[
\omega_r=\omega_n\sqrt{1-2\zeta^2}
\]
为谐振频率,因此,当\(\zeta<0.707\)时,需要对近似的波特图进行修正
进一步,谐振峰值\(M_r=\frac{1}{2\zeta \sqrt{1-\zeta^2}}\)
二者分别和阻尼频率和超调量有类似的表达式
相位响应曲线
\[
\phi = -\tan^{-1}\frac{2\zeta\frac{\omega}{\omega_n}}{1-\left(\frac{\omega}{\omega_n}\right)^2}
\]
在转角频率,\(\phi=-90^\circ\),与\(\zeta\)无关
画法和一阶类似,区别是从\(0^\circ\sim -180^\circ\)
5.2.2 最小相位系统
当系统函数的0极点都位于左半平面,且没有延迟因子\(e^{-j\omega T}\)时,系统是最小相位系统
在所有有相同幅度响应的系统中,最小相位系统的相角变化是最小的,因此,确定了幅度响应,就确定了一个最小相位系统
可以通过全通滤波器,将非最小相位系统转化为最小相位系统(0极点相消)
全通滤波器不改变幅值曲线,但是改变相角曲线
利用波特图判断
最小相位系统的波特图存在以下的性质,其中\(p,q\)分别是分子/母的次数
- \(\omega\rightarrow \infty \Rightarrow \angle H = -90^\circ(q-p)\)
- \(\omega\rightarrow \infty \Rightarrow -20(q-p)\)的斜率
这是充要条件,就是排除右边的0极点和延迟因子,也就是必须是\(\Pi(1+j\omega T_i)^{\pm1}\)的形式,其中\(T_i>0\)
5.2.3 延迟传递
\[ G(j\omega)=e^{-j\omega T} \]
幅值恒为1,相位\(\angle G = -\omega T\mathsf{rad} = -57.3 \omega T ^\circ\),在波特图上表现为指数函数
5.2.4 系统类型和幅值曲线的关系
在低频时,曲线的斜率只由纯积分因子决定
- 0型系统:水平线
- 1型系统:-20dB/十倍频
- 2型系统:-40dB/十倍频
下面的讨论都是针对的单位负反馈系统
0型系统
\[
\lim\limits_{\omega\rightarrow 0}G(j\omega) = K_p
\]
那么水平线的方程为
\[
y = 20\lg{K_p}
\]
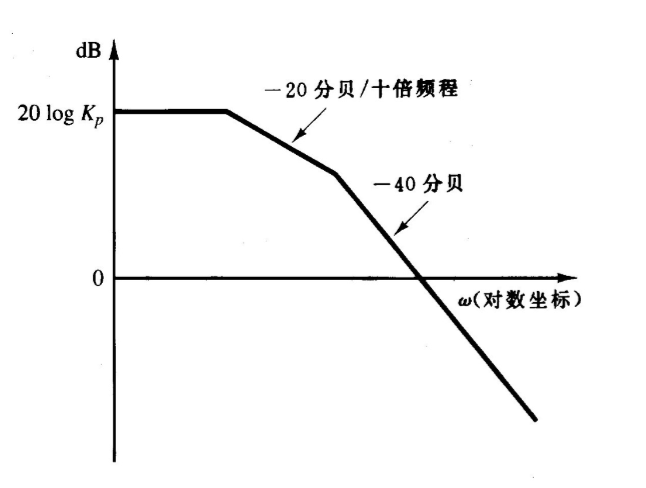
1型系统
低频时的曲线方程为
\[
y =20\lg{\frac{K_v}{\omega}}
\]
那么当\(\omega=1\)时,可以算出\(K_v\)
\[
y|_{\omega=1}=20\lg{K_v}
\]
当然也能通过\(y=0\)计算\(K_v\),当\(y=0\)时
\[
\omega_1 = K_v
\]
存在以下关系
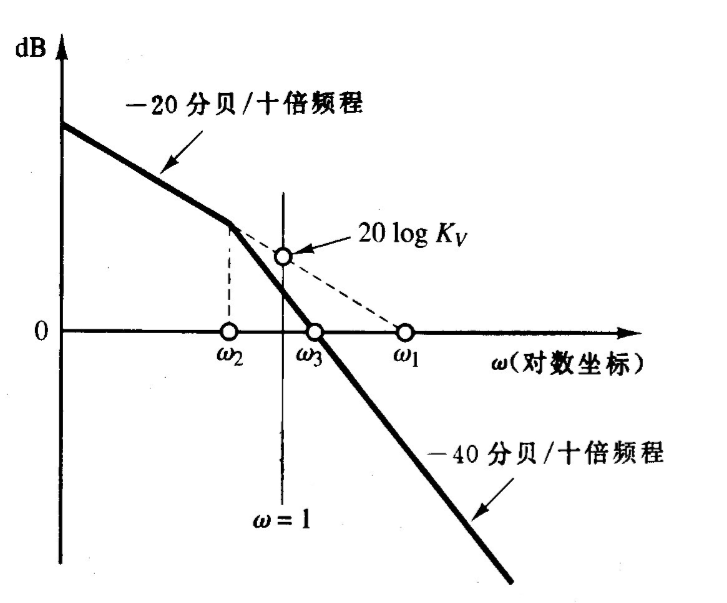
其中\(\lg\omega_2 +\lg{\omega_1} = 2\lg{\omega_3}\),且\(\zeta = \frac{\omega_2}{2\omega_3}\)
前者很好证明,\(\tan \omega_3= 2\tan\omega_1\),这里指图上对应的角度,而不是频率本身,那么\(|\lg\omega_2-\lg\omega_3|=|\lg\omega_3-\lg\omega_1|\)
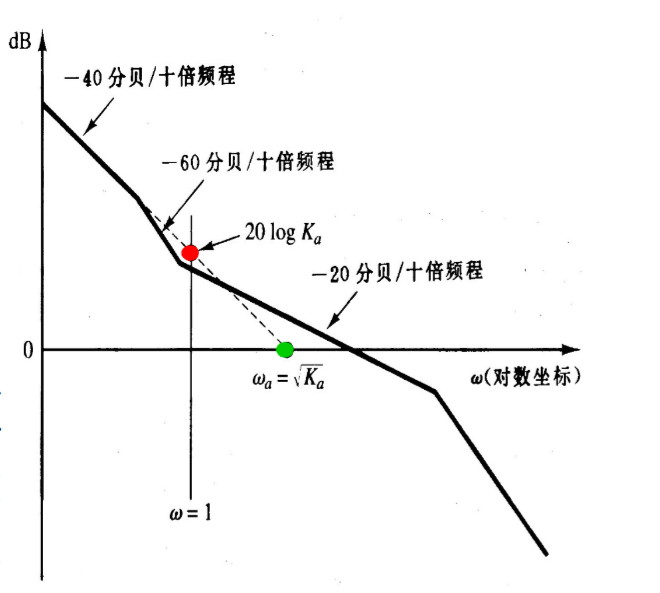
2型系统
低频时曲线的方程为
\[
y =20 \lg \frac{K_a}{\omega^2}
\]
当\(\omega = 1\)时,有
\[
y = 20\lg K_a
\]
同理,使用交点坐标也行,当\(y = 0\)时
\[
\omega_a = \sqrt{K_a}
\]
5.3 奈奎斯特图
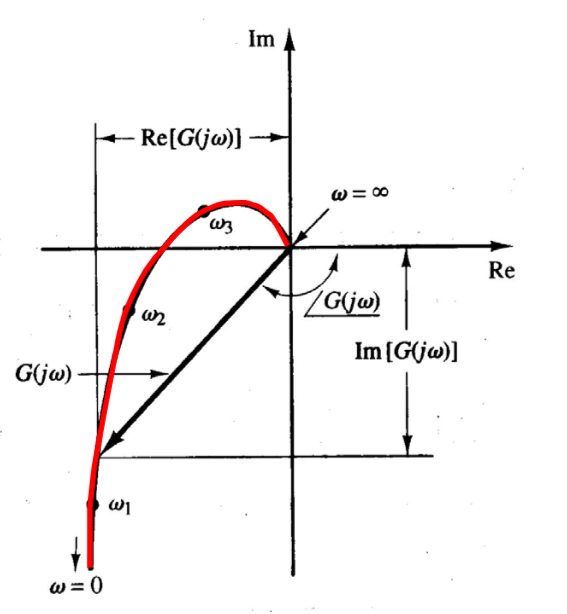
也叫极坐标图,但是注意此时的坐标轴是\(\mathsf{Re}\{G\},j\mathsf{Im}\{G\}\),而不是那个变换了空间的极坐标
将\(G(j\omega)\)表达为
\[
G = |G| e^{j\angle G}
\]
使用\((|G|, \angle G)\)表达传递函数,形如
5.3.1 积分和微分因子
积分因子
\[
G = \frac{1}{j\omega}
\]
拥有恒定的相位\(\angle G = -90^\circ\),幅值\(|G| = \frac{1}{\omega}\),故图像为负虚轴,但是注意\(\omega\)越小,\(|G|\)越大
微分因子
\[
G = j\omega
\]
拥有恒定的相位\(\angle G = 90^\circ\),幅值\(|G| = \omega\),故图像为正虚轴,\(\omega\)越大,\(|G|\)越大
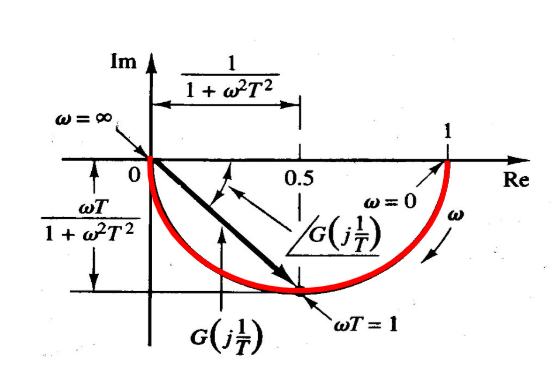
5.3.2 一阶因子
积分
\[
G = \frac{1}{1+j\omega T}
\]
\(\angle G = -\tan^{-1}\omega T, |G| = \frac{1}{\sqrt{1+\omega^2T^2}}\),在极坐标中表现为半圆,圆心位于\((0.5,0)\),半径为\(0.5\)
微分
\[
G = 1+j\omega T
\]
\(\angle G = \tan^{-1}\omega T, |G|=\sqrt{1+\omega^2T^2}\),表现为一条直线
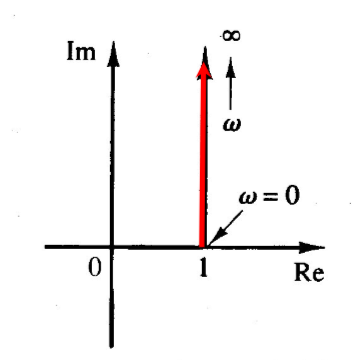
这张图中虚轴可以对应于\(\omega\),但只是巧合
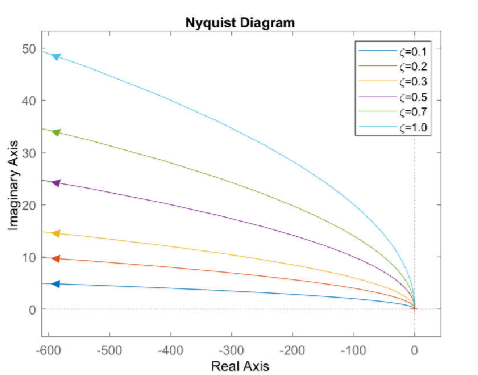
5.3.3 二阶因子
积分
\[
G = \frac{1}{1+2\zeta \left(\frac{j\omega}{\omega_n}\right)+\left( \frac{j\omega}{\omega_n} \right)^2}
\]
图不重要,只需要关注两个点\(G(j0),G(j\infty)\)即可
\[
G(j0)=1\angle 0,G(j\infty)=0\angle-\pi
\]
因此图大致如下
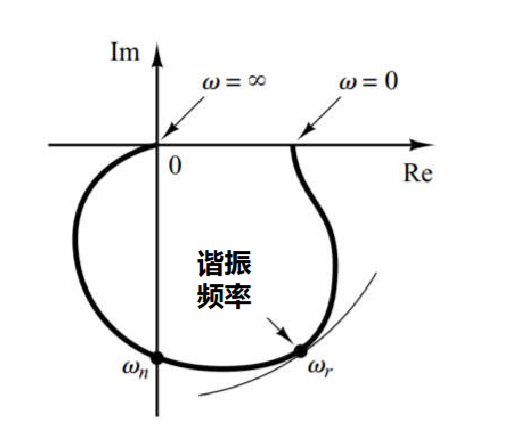
其中在虚轴上的点代表了自然频率处的幅值,幅值最大的点代表了谐振频率处的幅值
谐振频率处的幅值大小可以用1(即ω=0)来估计
上面的是\(\zeta<1\)的图,当\(\zeta>>1\)时,两个实轴上的极点相差很大,退化为类似1个极点的一阶因子图像,即一个半圆
微分
类似的,图像如下
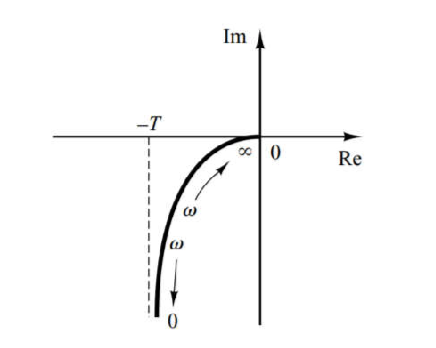
例:求\(G(s)=\frac{1}{s(Ts+1)}\)的奈奎斯特图
解:首先写成
\[
G = \frac{1}{\sqrt{\omega^4T^2+\omega^2}}\angle-\tan^{-1}\frac{1}{\omega T}
\]
光有这个不足以确定图像,还需要写出实部和虚部辅助判断
\[
\mathsf{Re}\{G\} = -\frac{T}{\omega^2T^2+1}\,\,\,\,,\mathsf{Im}\{G\} = -\frac{1}{\omega^3T^2 + \omega}
\]
由此可以画出
5.3.4 极坐标图的一般形状
假定传递函数形如
\[
G = \frac{K\Pi(1+j\omega T_a)}{(j\omega)^\lambda\Pi(1+j\omega T_b)} = \frac{\sum_{i=0}^m a_i(j\omega)^i}{\sum_{i=0}^n b_i(j\omega)^i}
\]
其中\(n>m\),这类函数的极坐标图存在以下性质
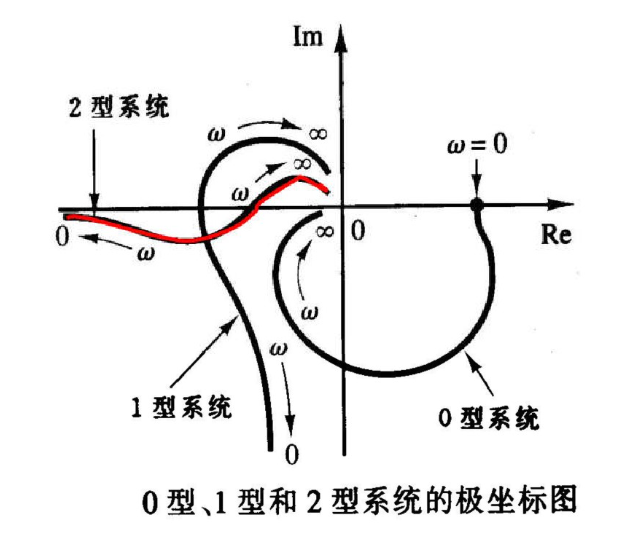
\(\lambda=0\),即0型系统
代入\(\omega=0\),得到\(G=K\in R\),即起点是正实轴上的一个有限值,发射角也与实轴垂直
代入\(\omega=\infty\),得到\(|G |= 0\),且与坐标轴相切
\(\lambda=1\),即1型系统
同理得到\(G(0)=-j\infty\),且渐近线是一条平行于负虚轴的线,代入\(\omega=\infty\),得到\(|G|= 0\),且与坐标轴相切
\(\lambda=2\),即2型系统
\(G(0)=-\infty\),从负实轴而来,相切于坐标轴
如何判断\(\omega=\infty\)时的切线
使用后一个式子,当\(\omega=\infty\)时,只需要考虑最高次,那么
\[
G = \frac{a_m(j\omega)^m}{b_n(j\omega)^n}\\
|G| = 0\\
\angle G = j^{m-n}
\]
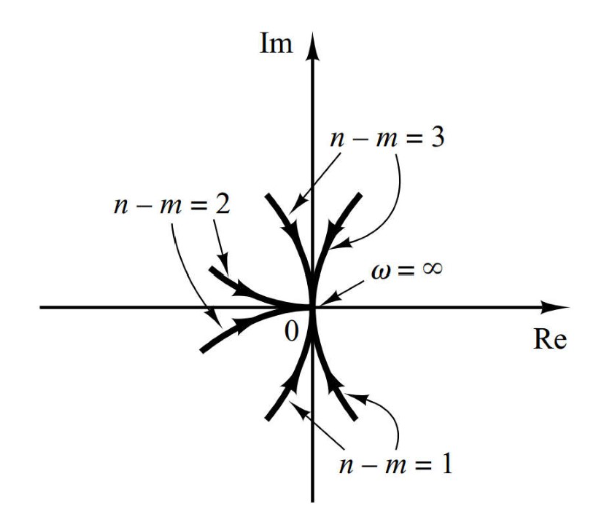
至于从哪边相切,无法确定
极坐标图的任何复杂形状都是由分子的动态特性引起的,即分子的时间常数
5.4 对数幅-相图
用分贝表示幅度和相位的关系图,也叫尼柯尔斯图
由于
\[
20\lg |G^{-1}| = -20\lg {G}\\
\angle G^{-1} = -\angle G
\]
那么在极坐标空间中,\(G\)和\(G^{-1}\)的尼柯尔斯图是关于原点对称的
不同于奈奎斯特图,这里真的是变换到极坐标空间了
画法就是根据波特图上的一个\(\omega\),对应的\(|G|,\angle G\),用函数\(|G| = F(\angle G)\)表示
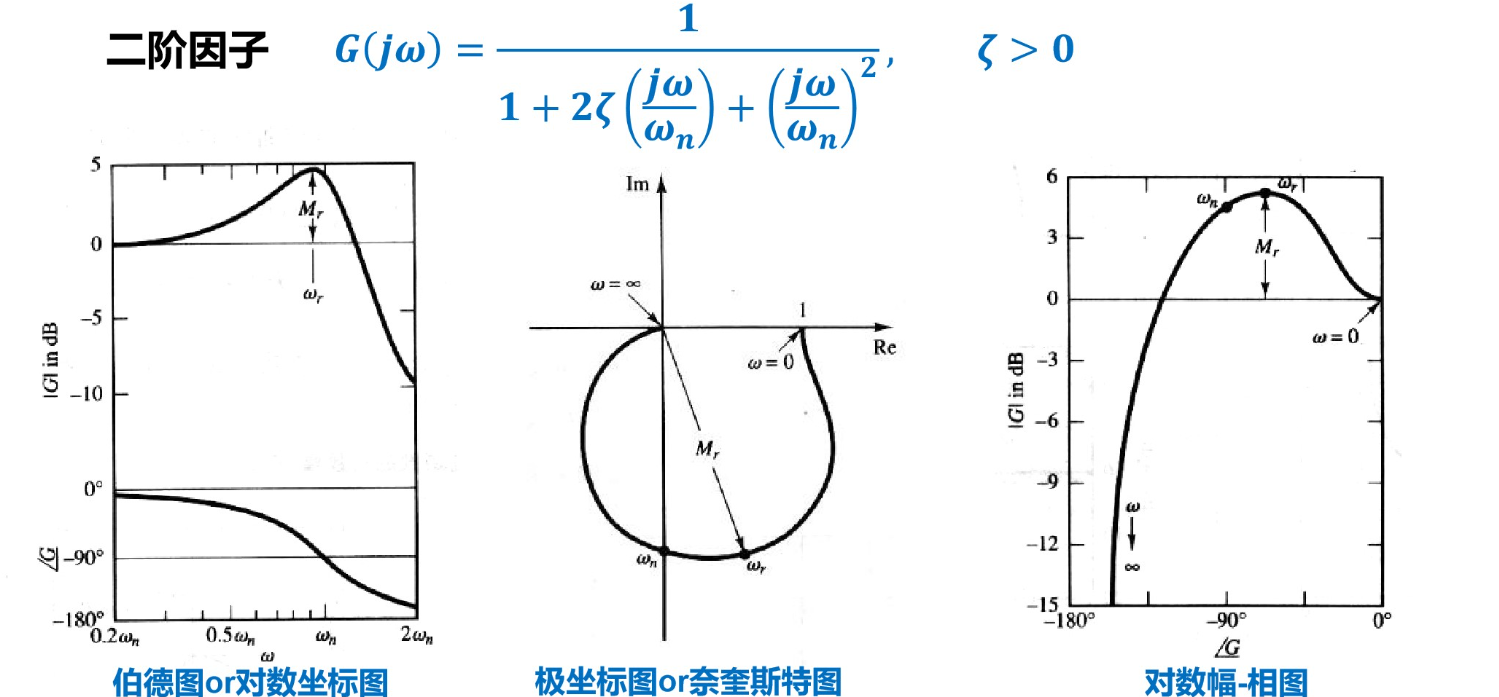
5.5 几幅图的对比
以二阶因子为例
5.6 奈奎斯特稳定判据
根据开环频率响应和开环极点确定系统的稳定性
即将\(GH\)与\(1+GH\)在右半平面的0极点数相联系
5.6.1 基本概念
对于特征函数
\[
F(s) = 1+G(s)H(s)
\]
可以得到下面的表格
| s平面的特殊点 | F(s)的特殊点 |
|---|---|
| 闭环极点 | 0点 |
| 开环极点 | 极点 |
不加证明,直接引入下面的定理
函数\(F(s)\)在\(s\)平面上除了奇点外,处处解析
对于\(s\)平面上的任一条闭合曲线(变量是\(s=\sigma+j\omega\)),在\(F(s)\)平面上一定有一条对应的闭合曲线(变量是\(\mathsf{Re}\{GH\},\mathsf{Im}\{GH\}\))
\(s\)平面上的曲线顺时针经过\(Z\)个\(F(s)\)的0点(闭环极点),\(P\)个\(F(s)\)的极点(开环极点)
那么在\(F(s)\)平面上,对应一条封闭曲线,顺时针包围原点\(N=Z-P\)次,\(N<0\)表示逆时针
由于\(F(s)\)的0点就是系统的闭环极点,是否能够通过上面的性质进行稳定性判定?
系统稳定等价于传递函数收敛域包含虚轴,由于这里讨论的都是有理分式,故等价于\(s\)平面的右半平面没有极点
即:系统稳定等价于\(F(s)\)在\(s\)的右半平面没有0点
由于\(Z=N+P\),后二者是好算的
可以构造一个\(s\)平面的曲线,让\(Z\)表示在右半平面的0点,即一个半径无限的半圆
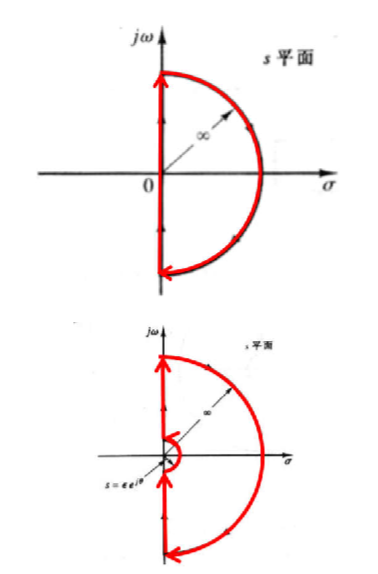
下方的图表示\(s=0\)是0/极点的情况,做一个小圆绕过去
为了顺时针,\(s\)平面是从\(0-j\infty\)到\(0+j\infty\),再回到\(0-j\infty\),这就是\(\omega\)的变化过程
由于\(\lim\limits_{s\rightarrow \infty}GH=\mathsf{const}\in \R\),故在圆弧段的所有\(s\)对应在\(F(s)\)的一个点(实轴上,包含0),在\(\omega\)从\(-\infty\)到\(+\infty\)对应的是主要的曲线
即只需要考虑\(\omega\)的变化,那么就回到了奈奎斯特图
再考虑\(F(s)=1+GH\)对原点的包围,等价于\(GH\)对\(-1+0j\)的包围
又由于\(G,H\)的各自的共轭对称性,存在\(G(j\omega)H(j\omega)=G(-j\omega)H(-j\omega)\),因此只需要画一半就行
5.6.2 奈奎斯特稳定判据
这个东西看着鸡肋,但是当系统函数不显式时是比较好用的
根据上面的讨论,当\(GH\)顺时针包围\(-1\,\,\,N\)次时,系统的右半平面的闭环极点个数为\(N+P\)
那么为了系统稳定,\(GH\)需要逆时针包围\(-1\,\,\,P\)次
如果通过\(-1\),说明系统存在纯虚的闭环极点,系统临界稳定
例:\(GH=\frac{K}{s(Ts+1)}\),判断是否稳定
解:\(P=0\),需要画奈奎斯特图,由于
\[
\mathsf{Re}\{GH\} = -\frac{T}{\omega^2T^2+1}\,\,\,\,,\mathsf{Im}\{GH\} = -\frac{1}{\omega^3T^2 + \omega}
\]
故部分的曲线形如

注意这里的\(0\)指的是\(0^+\),相应的,关于实轴对称后得到\(\omega:-\infty\rightarrow 0^-\)的图像,那么还有\(0^-\rightarrow0^+\)的图像呢?
由于这个函数的极点在0上,需要对\(s\)平面上的曲线进行取小圆弧,令这段圆弧为
\[
s=\sigma+j\omega = \varepsilon e^{j\theta} = \varepsilon\cos\theta + j\varepsilon\sin\theta
\]
其中\(\sigma\rightarrow 0,\varepsilon\rightarrow 0, \theta:-90^\circ\rightarrow 90^\circ\)
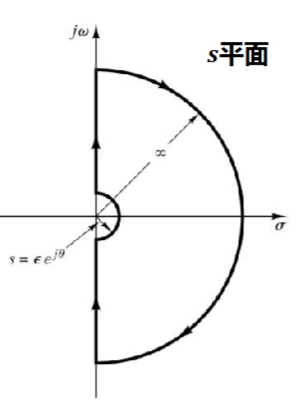
那么这部分的\(GH = \frac{K}{\varepsilon}e^{-j\theta}\),由于我们需要\(\omega:0^-\rightarrow0^+\),而\(\omega=\varepsilon \sin\theta\),那么就是前面\(\omega\)的取值变化对应于\(\theta\)就是\(\theta:-90^\circ\rightarrow 90^\circ\)
那么\(GH\)在奈奎斯特图中表现为
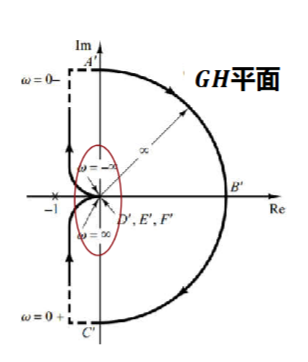
图中的无限半径的圆弧就是\(s\)平面上这一小段圆弧产生的
根据\(s\)平面的顺时针方向,即\(\omega:-\infty\rightarrow +\infty\rightarrow -\infty\),来确定\(GH\)的方向,上图中\(N=0\),系统稳定
补:对于包含积分因子\(\frac{1}{s^n}\)的\(GH\),\(s\)沿小圆运动会产生n个上面的圆环绕原点,没什么用
5.7 相对稳定性
以下的讨论默认系统具有单位负反馈,且是最小相位系统(没有右边的0/极点)
5.7.1 通过保角变换进行相对稳定性分析
将\(s\)平面的虚轴映射为\(GH\)平面的奈奎斯特轨迹,那么将得到
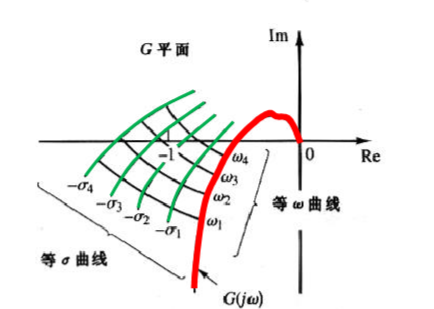
由此,将 闭环极点距离虚轴的距离 转换为 \(GH\)曲线距离\(-1+j0\) 的距离
后者越小,那么前者也越小,系统的\(\zeta\)也就越小,那么系统的瞬态响应和稳态响应也对应变化
当然二者同时也表征了相对稳定性
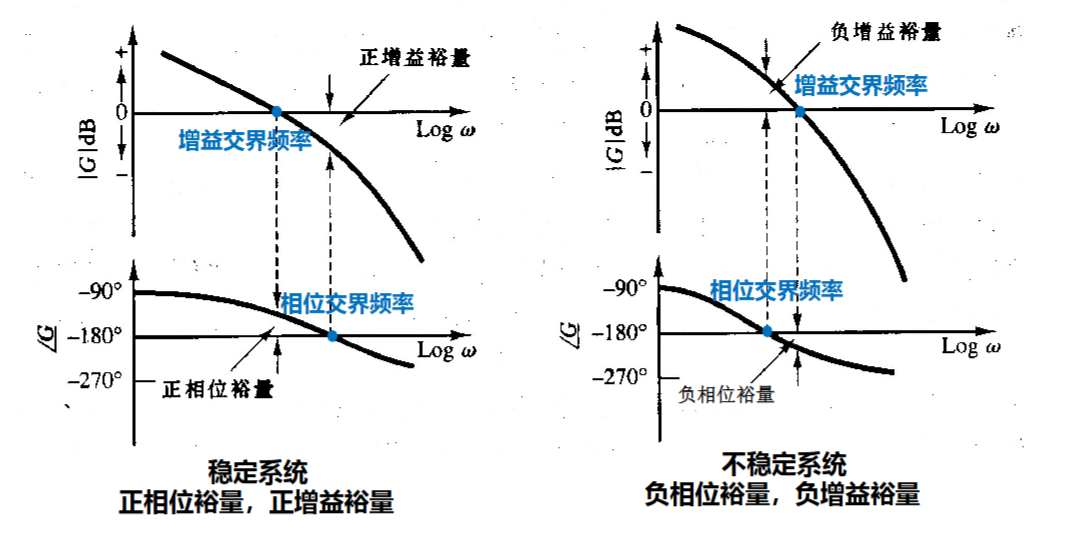
5.7.2 相位裕量和增益裕量
几个定义
增益交界频率:\(|GH|=1\)时的频率
相位裕量:在\(|GH|=1\)时,\(\angle GH\)与-180°的差值,即\(\angle GH -\gamma =-180^\circ\Rightarrow \gamma =\angle GH +180^\circ\)
通常\(\angle GH\)用顺时针的负角度表示,即\(240^\circ = -120^\circ\)
很显然,为了使最小相位系统稳定,\(\gamma\)必须是正的
相位交界频率:\(\angle GH =-\pi\)时的频率
增益裕量:\(\angle GH=-\pi\)时,\(K_g=\frac{1}{|GH|}\),一般用dB表示,\(K_g(\mathsf{dB})=20\lg K_g=-20\lg{|GH|}\)
若\(K_g>1\),在奈奎斯特图上表现为与实轴的交点在单位圆内,系统稳定
\(K_g<1\),系统不稳定
为什么需要先取倒数?:可以将其理解为\(|GH|<1\)是否成立,当起在\(\angle GH=-\pi\)成立时,说明不包围\(-1+j0\),那么为了和相位裕量统一,都定义为正值,就取倒数后再取对数;或者直接理解为\((0-20\lg|GH|)\),这种语境下,相位裕度就是\(\angle GH -(-180^\circ)\)
相位裕量和增益裕量在波特图中是最好看的
实际上在对数幅-相位图更好看
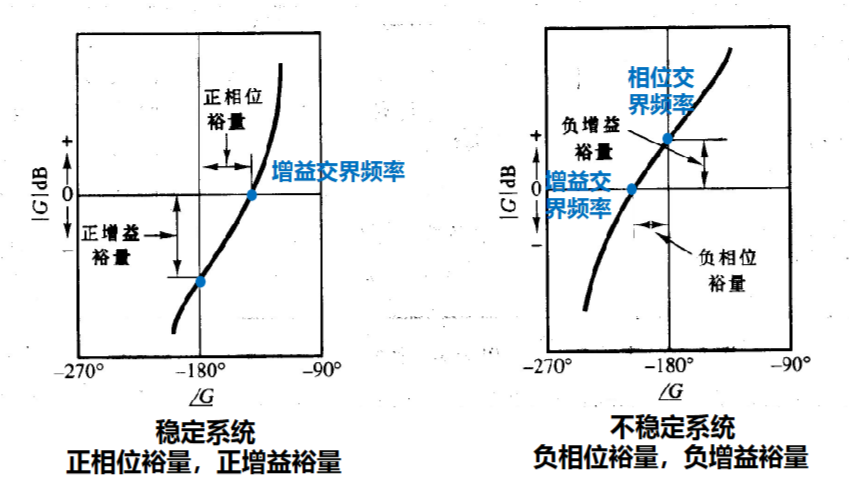
几点补充
对于条件稳定的非最小相位系统,由于其存在右边的0/极点,奈奎斯特图必须包围(分情况顺逆时针)\(-1\)
因此这个系统一定是负的相位和增益裕度
条件稳定系统具有多个相位交界频率,对于存在多个增益交界频率的系统,在计算相位裕量时用最大的频率
为了确定系统的相对稳定性,增益和相位裕量必须同时给出
对于最小相位系统,只有二者同时是正值时才稳定
确定非最小系统稳定性的最好办法,是奈奎斯特判据
5.7.3 谐振峰值和谐振峰值频率
谐振峰值幅度:表征了系统的相对稳定性
- 大的谐振峰值表示存在一对主导闭环极点,且具有较小的\(\zeta\),瞬态响应不理想
- 小的,不存在,有较大的\(\zeta\),阻尼比较良好
联系二阶系统的最大过调量和阻尼频率,可以发现频率响应的系统动态信息和瞬态响应的信息是相同的
当\(\zeta\)较小时,谐振频率与阻尼自然频率相近,因此,谐振频率可以代表响应速度
\(\zeta\)越小,谐振峰值\(M_r\)和超调量\(M_p\)就越大,当\(M_r\in [0,3]\mathsf{dB}\)时,表示\(0.4<\zeta<0.7\),系统有满意的瞬态
相位裕量与阻尼比的关系
当\(0\leq \zeta \leq 0.6\)时,\(\zeta = \frac{\gamma}{100}\)
5.7.4 截止频率和带宽
当闭环响应的幅值降到-3dB时,认为系统截止,对应的频率称为截止频率\(\omega_b\),也就是带宽
带宽的性质
- 与\(\zeta\)成反比,与上升时间反比,与响应速度成正比
- 反映对高频噪声的过滤
剪切率:对数幅值曲线在截止频率附近的斜率,如-20dB/十倍频等
反映了系统的抗干扰能力,越大,系统可能有大的谐振峰值,小的稳定裕度
不严谨的理解,可以理解为变化很快,说明变化很大,说明谐振峰值很大,说明\(\zeta\)小,根据\(\zeta = \gamma/100\)进一步说明稳定裕度很小
5.8 单位反馈系统的闭环频率响应
注意是闭环,如何构造呢
\[
\frac{C}{R} = \frac{G}{1+G}
\]
根据0极点图的想法,将上下视为向量
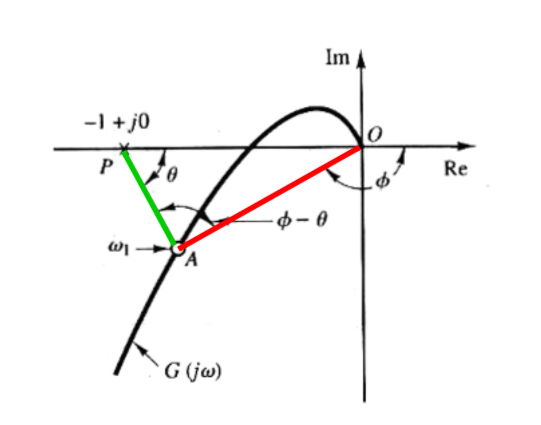
下面的就是\(G-(-1)\)
令\(G = X+jY\),再令\(\frac{C}{R} = Me^{j\alpha}\),那么
\[
M = \left|\frac{X+jY}{X+1+jY}\right| \Rightarrow \left( X+\frac{M^2}{M^2-1} \right)^2+Y^2 = \frac{M^2}{(M^2-1)^2}\,\,,\,\, M\neq 1
\]
当\(X=-\frac{1}{2}\)时,\(M=1\)
根据上面的方程可以确定等幅值轨迹
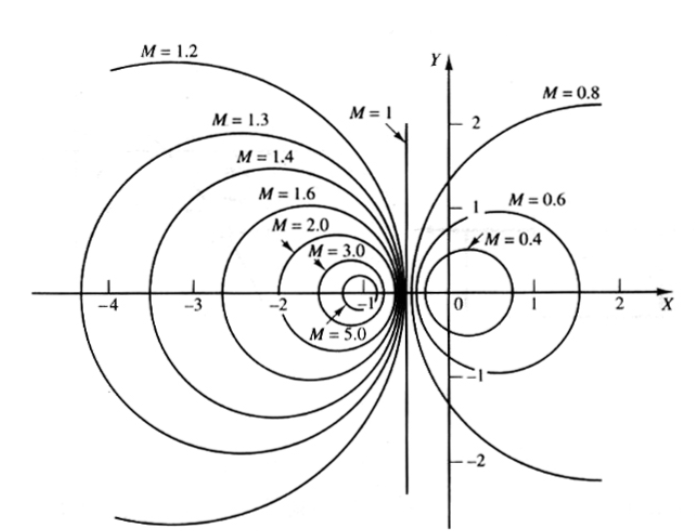
同理,令\(N=\tan \alpha\),那么
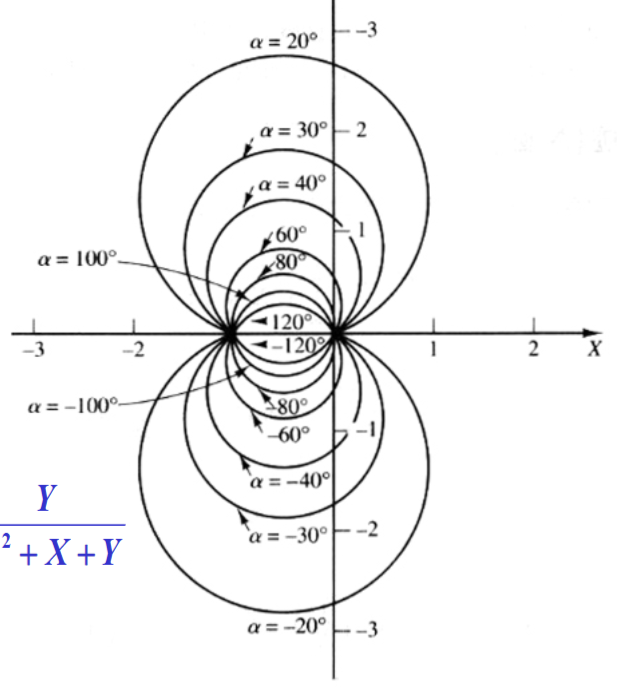
\[
N = \frac{Y}{X^2+X+Y}\Rightarrow \left( X+\frac{1}{2} \right)^2+\left( Y-\frac{1}{2N} \right)^2 = \frac{1}{4}+\frac{1}{4N^2}
\]
根据上面的方程,确定等辐角轨迹
这些轨迹都存在于\(\mathsf{Re,Im}\)空间,也就是奈奎斯特图的空间,在这些图上叠加\(G\)的奈奎斯特图,得到
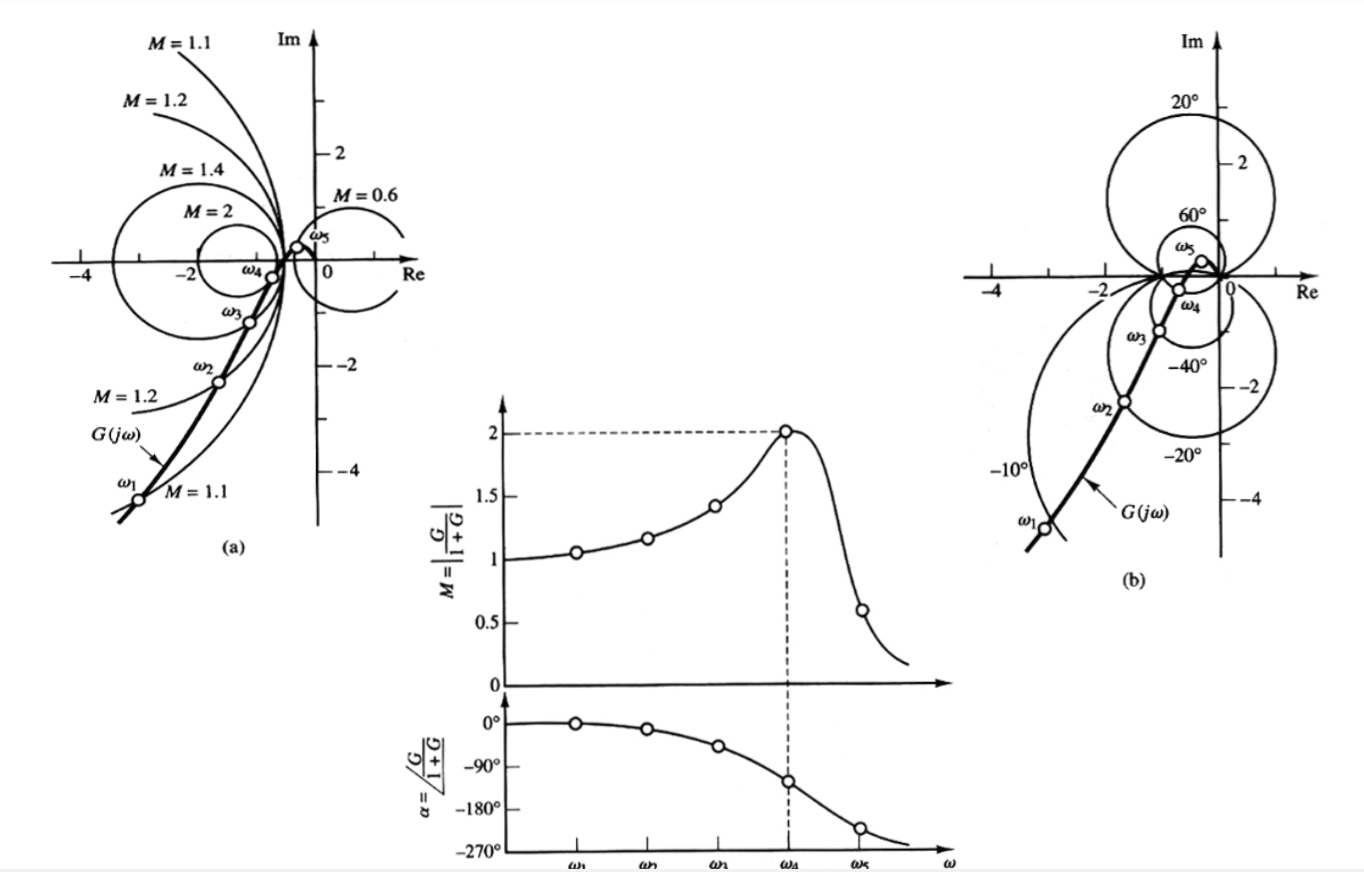
交点表示对应频率下的闭环函数的特征,由此可以得出闭环传递函数的尼科尔斯图(对数幅-相图)
如果和\(G\)有切点,那么相切代表谐振,切点的频率就是谐振频率:观察尼科尔斯图可以发现,谐振频率就是最高的,也就是仅一个\(\omega\)对应,那么就是切点
5.9 有波特图求最小相位的传递函数
只能求最小相位,而且波特图必须以渐近线的形式给出
很显然,对于最小相位系统,传递因子只包括了5.2节中提到的那些,只需要根据这些因子的特性进行反推就行
阻尼比可以根据谐振峰值的大小进行估计
增益的确定见5.2.4节,那里讲了不同系统的\(K\)的对应值
非最小相位系统,不好搞,不要求
5.10 系统矫正
使用波特图居多,因为只需要平移图像就好了
奈奎斯特图的变化非常复杂
开环响应的轨迹反应了什么?
- 在低频区(远低于转角频率),表征闭环系统的稳态特征
- 在中频区(靠近\(-1+j0\)),表征闭环相对稳定性
- 在高频区,表征系统的复杂性
5.10.1 超前矫正
超前矫正函数见4.4.2节,这里给出其正弦传递函数
\[
G_1(j\omega) = K_c\alpha \frac{1+j\omega T}{1+j\alpha\omega T}\,\,,\,\,\alpha\in(0,1)
\]
做出其极坐标图
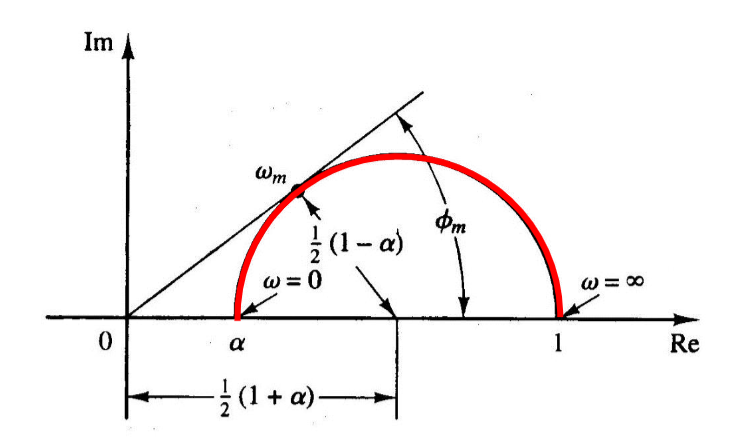
那么能提供的最大超前角就是
\[
\sin \phi_m = \frac{1-\alpha}{1+\alpha}
\]
做出波特图,可以发现提供最大超前角的频率为
\[
\omega_m = \frac{1}{\sqrt{a}T}
\]
由于超前矫正给系统带来了正的幅值,使得增益交界频率向右移动,减小了相位裕度
因此,最大超前角必须在原有的相位裕度上增加5°
如果在增益交界频率附近,相角减小很快,那么超前校正将无效,因为很难在右移的同时产生足够的相位裕度
为了产生足够的相位裕度,\(\alpha\)将会很小,但是这个值做不到很小
如果需要\(\phi_m>65\)°,需要考虑多个超前矫正串联
超前矫正使得系统的带宽变大,瞬态响应变好
5.10.2 滞后矫正
其传递函数为
\[
G_c(s) = K_c\beta \frac{Ts+1}{\beta Ts+1}\,\,,\,\, \beta\in (1,+\infty)
\]
其极坐标图为
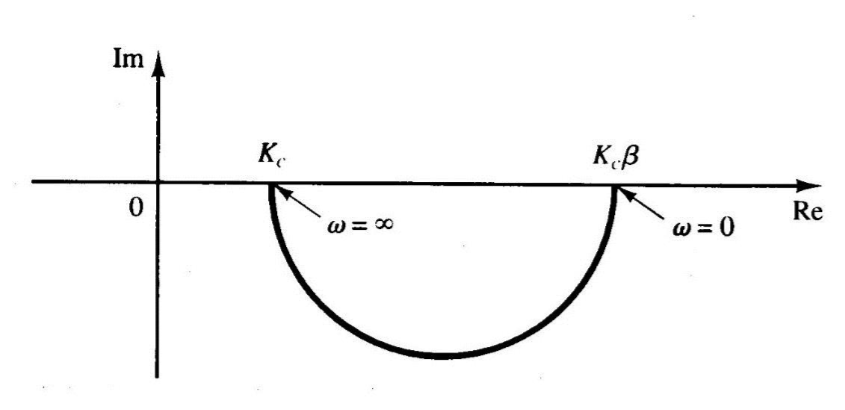
根据波特图发现滞后矫正器本质是一个低通滤波器,存在一个\(20(\lg\frac{1}{\beta T} - \lg\frac{1}{T})=-20\lg\beta\)的下降,这就是用来重新确定增益交界频率的,也就是将增益交界频率向低频处移动,这样会降低系统的带宽,导致瞬态响应变差,但结果是增大了相位裕量
其主要作用是在高频段造成衰减,使系统获得足够的相位裕量
但是由于滞后矫正本身会引入一个相位滞后,因此在设计时要多加5°-12°的裕量
且为了防止滞后的相位的影响,配置的0极点必须要至少远离新增的增益交接频率10倍频
5.10.3 滞后-超前矫正
先滞后,后超前
\[
G_c(s) = K_c\frac{\beta}{\gamma}\left( \frac{T_1s+1}{\frac{T_1}{\gamma}s+1} \right)\left( \frac{T_2s+1}{\beta T_2s+1} \right)\,\,,\,\, \gamma,\beta >1
\]
可选\(\gamma = \beta\)
5.10.4 三者的比较
超前矫正
- 主要用于改善稳定裕量
- 系统带宽更大,瞬态响应好
- 但对高频噪声更敏感
- 需要附加的增益增量来补偿超前网络的衰减
滞后矫正
- 通过高频衰减特性进行增益交接频率的重新确定,来改善相位裕量
- 系统带宽更小,瞬态响应变差
- 降低了高频增益,系统的总增益可以变大,低频的增益可以变大,系统的稳态精度更好
滞后-超前矫正
- 瞬态响应快,稳态精度高
- 低频增益变大,带宽百年大,稳定裕度也变大
5.10.5 不希望极点的抵消
通过串联0点,但是
- 几乎不可能完全抵消
- 未完全抵消的0极点产生一个持续时间长,幅度很小的瞬态响应分量