4 根轨迹分析
一种用图解方法表示特征方程的根与系统某个参数的全部值的关系的方法
简言之,用开环0/极点,表示对闭环0/极点的影响
使开环传递函数\(GH = -1\)的解,也就是\(GH+1 = 0\),解出的\(s\)是闭环传递函数的极点
4.1 根轨迹图
4.1.1 辐角和幅值
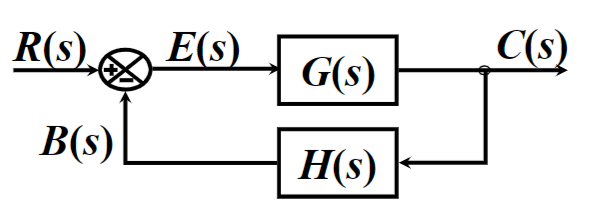
闭环传递函数为
\[
\frac{C}{R} = \frac{G}{1+GH}
\]
特征方程为
\[
GH+1=0\\
GH = -1
\]
满足条件的解和下面的方程相同
\[
|GH| = 1\\
\angle{GH} = (2k+1)\pi
\]
分别是幅值条件和辐角条件,满足上述条件的\(s_i\)就是闭环极点,只满足辐角条件的点构成的图形就是根轨迹,这个轨迹上满足幅值条件的点就是闭环极点
一般\(GH = \frac{K\cdot \Pi (s+z_i)}{\Pi(s+p_j)}\),其中\(K\)是增益参数,方程可以写为
\[
K\cdot \Pi(s+z_i) + \Pi(s+p_j) =0
\]
当\(K\)从0增大到\(\infty\)时,开环0点的作用变大,开环极点的作用变小,故根轨迹始于开环极点,终于开环0点,但是轨迹是闭环极点的轨迹
关于这里到底是+0/极点的负数,还是直接-0/极点,看个人喜好,这里用+只是因为图片内是+而我不好修改
对于
\[
GH = \frac{K(s+z)}{(s+p_1)(s+p_2)(s+p_3)(s+p_4)}
\]
而言,辐角为
\[
\angle{GH} = \varphi_1-\theta_1-\theta_2-\theta_3-\theta_4
\]
幅值为
\[
|GH|= \frac{KB}{A_1A_2A_3A_4}
\]
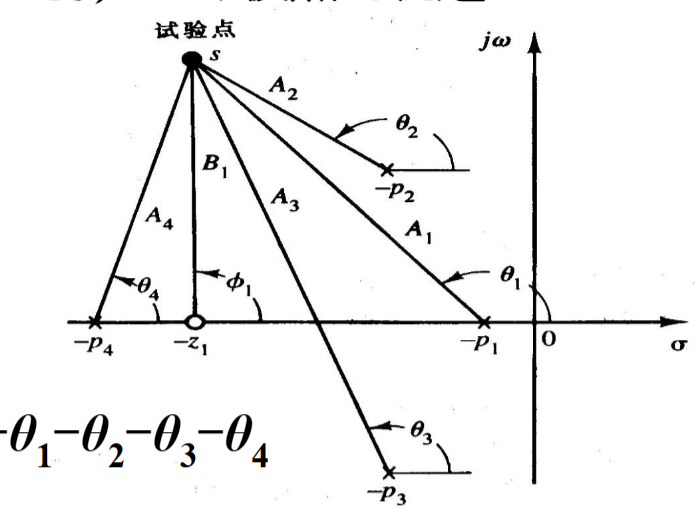
图中都是开环0/极点
4.2 根轨迹图解计算法
以下面这个为例
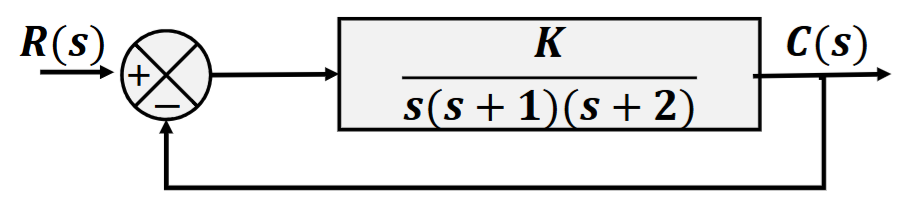
\[ G = \frac{K}{s(s+1)(s+2)}\\ p_1 = 0,p_2 = -1, p_2 = -2 \]
4.2.1 画出0/极点,确定辐角轨迹
根轨迹的起点就是极点,根轨迹的数目就是开环极点数目(也就是闭环极点数目)
上面有三个开环极点,说明有三条根轨迹
m条根轨迹终于开环0点,n-m条根轨迹终于无限远点
实轴上的根轨迹满足其右边区域有奇数个开环0/极点之和
在实轴上,符合辐角条件的区域有:\((-\infty,-2), (-1,0)\),这是根轨迹的一部分
完整的轨迹不好找,但是轨迹的渐近线是可以找的
渐近线一定满足辐角条件,即\(\lim\limits_{s\rightarrow \infty}\angle G(s) =(2k+1)\pi\),而\(\lim\limits_{s\rightarrow \infty}\angle G(s)=\angle\frac{Ks^M}{s^N} = (N-M)\angle s\)
得到渐近线的倾角
\[
\phi = \frac{(2k+1)\pi}{N-M}
\]
渐近线与实轴的交点则为(推导复杂,用到了我看不懂的近似方法,大致可以理解为这就是0/极点的重心)
\[ \sigma = \frac{\sum p_i- \sum z_i}{N-M} \]
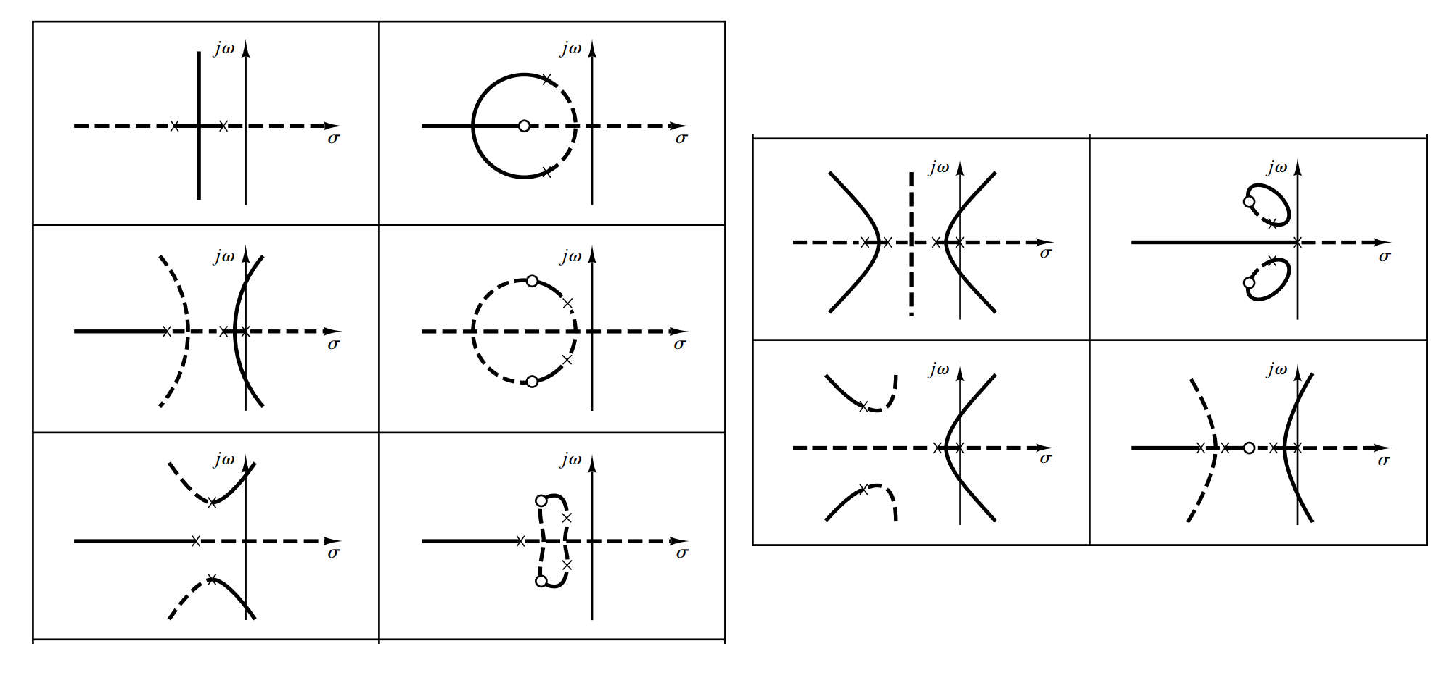
一般来说渐近线只有这几种情况(N=2时只有竖线,图画错了)
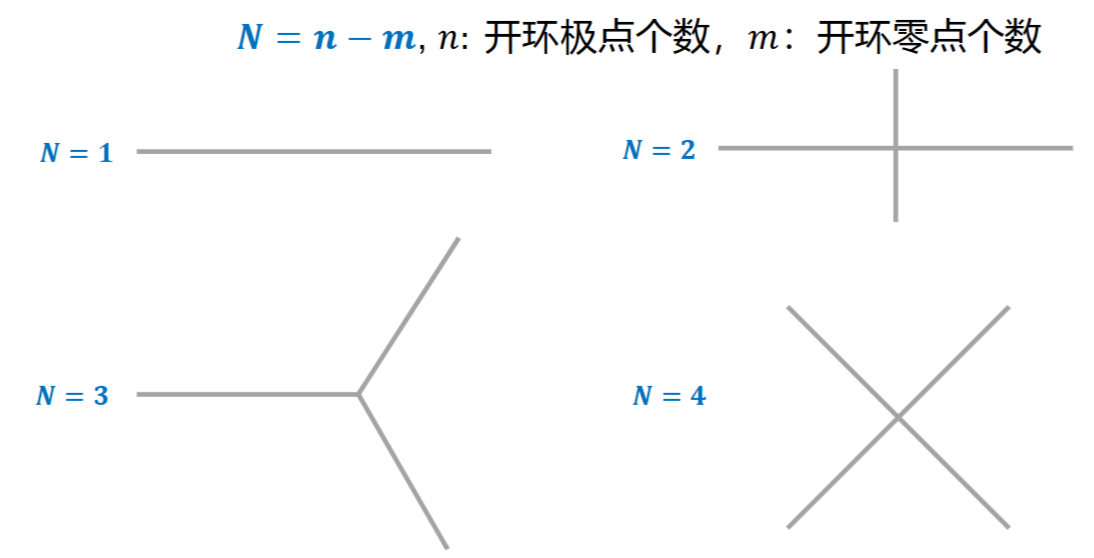
第一阶段结束,得到下图
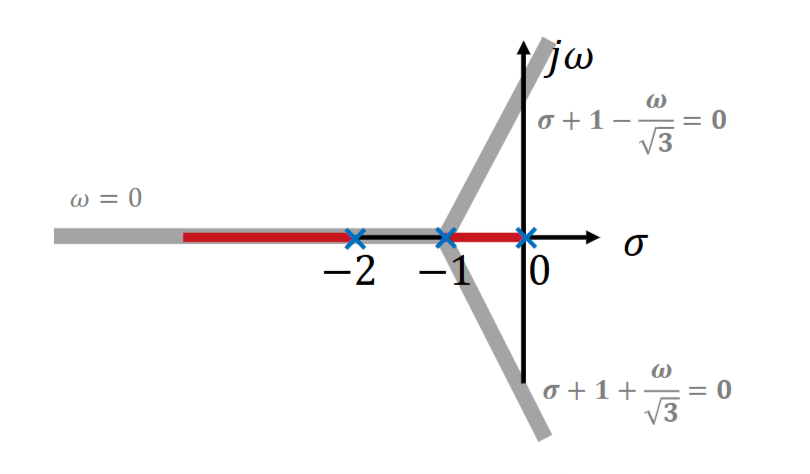
4.2.2 确定分离点
根轨迹从极点出发,在满足辐角条件的地方汇合并分离,上图的\((-1,0)\)之间就存在一个分离点
将特征方程写为
\[
f(s) = B(s) + KA(s) = 0
\]
而分离点就是是同时存在于多条根轨迹上的点,那么就是特征方程的重根
显然\(f(s) = \Pi(s-s_i)\),为了求得重根可以求使得\(\frac{df}{ds} = 0\)的点,或者令\(K = -\frac{B(s)}{A(s)}\),这些点等价于
\[
\frac{dK}{ds} = 0\Rightarrow BA^{'} - B^{'}A = 0
\]
注意不是所有的满足条件的解都是分离点,判断方法如下
- s在某条根轨迹上,那么一定是
- s对应的K为正值(K>0),那么一定是
其他都不是
分离点上根轨迹的切线的角度与在该点上相遇的根轨迹数目\(\gamma\)有关
\[
\phi_b = \frac{\pi}{\gamma}
\]
对本例,\(s_1 = -0.4226, s_2 = -1.5774\),对应\(K_1 = 0.3849, K_2 = -0.3849\),舍弃\(s_2\)
将分离点添加,指出对应的\(s,K\),在同一个实轴上的区间从极点开始向分离点靠拢,然后向渐近线走
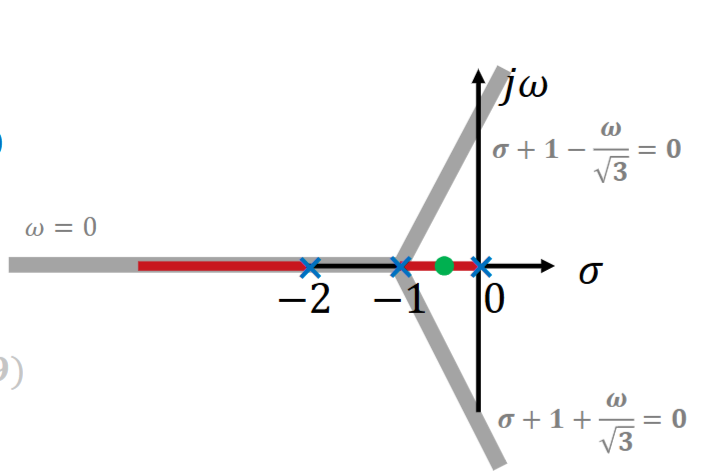
4.2.3 确定根轨迹和虚轴的交点
很显然一个稳定的系统收敛域必须包括虚轴,当存在渐近线穿过虚轴时,说明一定存在使系统不稳定的增益
沿远离极点的方向是K增大的方向,按正确的区间得到使得系统稳定的K区间
这有两个办法,第一个就是用劳斯判据,不赘述,得到\(0 第二个就是令\(s=j\omega\),带入特征方程,解出临界稳定的\(K\) 方法二的好处就是可以得到具体的K和临界解ω 出射角指的是开环极点上的根轨迹切线的角度 为了确定这个值,在开环极点附近做试验 那么其他点的辐角都能确定,根据辐角条件出射角满足 很显然,共轭极点退化为\(k\)重根后,出射角就是\(k\theta_1 = (2n+1)\pi -\theta_2 +\varphi_1\) 得到完整的根轨迹 注意此时求的是闭环极点,这个主导极点需要让系统有好的瞬态响应,也就是\(\zeta = 0.5\) 而\(\sigma = \zeta\omega_n, \omega_d = \omega_d\sqrt{1-\zeta^2}\),主导极点可以表示为\(s_i = -\sigma \pm j\omega_d\),一定在斜率为\(\pm\sqrt{3}\)的直线上 对于本例,已知\(\zeta, G(s)\),解得\(s_1,s_2\),通过幅值条件求的对应的K值 由于\(\left| \frac{K\Pi(s-z_i)}{\Pi(s-p_i)} \right| = 1\),代入上面的\(s_{1,2}\),由于共轭代一个就行,得到 主导极点是离虚轴近的那个/对,这就是为什么要求个\(s_3\)出来 这是一个存在0点的例子 \[
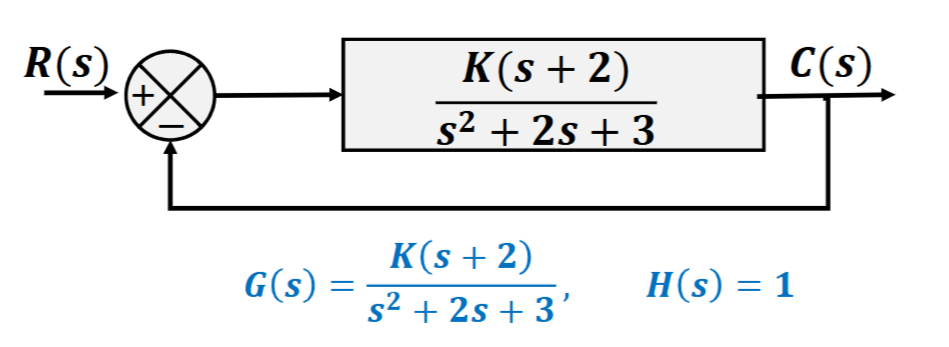
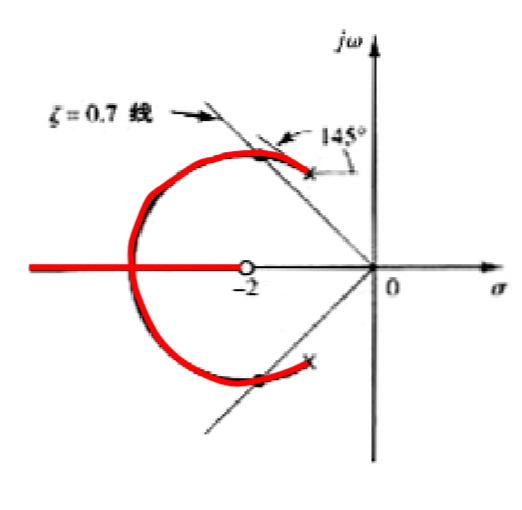
p_1 = -1+j\sqrt2 ,p_2 = -1-j\sqrt2, z=-2
\] 实轴上符合辐角条件的区域为\((-\infty, -2)\),和显然两条根轨迹一条走向\(-\infty\),一条走向\(-2\) 计算渐近线的斜率和实轴交点均为0,说明渐近线就是实轴 确定分离点,得到\(s=-3.7320, K =5.4641\) 确定出射角,都是\(145^\circ\) 确定分离点的切线斜率,带入γ=2,得到90° 最终图像为 由于这个轨迹和60°斜线不相交,换一个ζ 系统的闭环特征多项式可以写为 例:如图 确定闭环主导极点,使得\(\zeta=0.4\) 解:先解开内层循环,得到\(G_1(s)=\frac{20}{(s+1)(s+4)+20k}\),再和\(\frac{1}{s}\)相乘得到\(G_2(s)=\frac{20}{s(s+1)(s+4)+20ks}\) 这不是一个标准的形式,问题不大,先写出\(1+GH=0\),得到\(s(s+1)(s+4)+20ks+20=0\),除以\(s(s+1)(s+4)+20\)得到 最终得到的的根轨迹和\(\zeta=0.4\)的交点为 发现由于闭环主导极点不同,虽然\(\zeta\)相同,但是图像的形状不同 考虑特征方程 系统的开环0极点都在左半平面且没有传递延迟因子,则系统是一个最小相位系统;反之则不是 对于一个非最小相位系统 这样就导致了辐角条件改变为 特征方程变为 同样的传递函数,对于正负反馈系统来说,根轨迹往往是互补的 图中虚线是正反馈,实线是负反馈 正反馈系统在\(K\)增大时往往更容易不稳定 当\(K\)的取值对应于不稳定的工作状态,系统可能不稳定;或是存在非线性的因素,饱和之后系统非线性 这类系统叫做条件稳定系统 增加矫正网络 存在一个\(e^{-st}\),这使得相位变成了\(\omega\)的函数,系统变得很复杂,不要求 通过在开环传递函数中增加0极点,改变根轨迹的形状,使得根轨迹通过希望的的闭环极点(主导极点) 增加极点的影响 极点一定是增加在左边的,不然系统不稳定了 很显然在左边的极点会使得根轨迹右移, 系统将变得不稳定,同时调整时间(\(\frac{1}{\sigma}\))也会增加(闭环极点的实部减小,调整时间为实部的倒数) 增加零点的影响 根轨迹左移,系统变得稳定,调整时间减小 为了找到满意的闭环极点而使用,提高瞬态响应性能 为系统串联一项 例:单位负反馈系统的开环传递函数\(G(s)=\frac{4}{s(s+2)}\),要求不改变闭环极点的阻尼比,使\(\omega_n\)变为4 解:闭环极点的期望位置是\(-2\pm j2\sqrt3\),由于共轭,只需要考虑上面的极点,将这个值代入\(GH\)中,得到的辐角为\(-210^\circ\),与辐角条件相差\(30^\circ\),辐角缺额条件就是后者,故\(\angle{s+\frac{1}{T}} - \angle {s+\frac{1}{\alpha T}} = 30^\circ\),有很多组解,都行 这里选择\(\frac{1}{T} = 2.9,\frac{1}{\alpha T}=5.4\),这是\(G_c\)的0/极点,代入\(|G_c(s_1)G(s_1)|=1\),解出\(K_c=4.68\) 滞后矫正减小了稳态误差,提高稳态响应性能 为系统串联 与超前矫正不同,滞后矫正是因为系统没有满意的稳态特性,但是有较好的瞬态特性 因此为了不让瞬态特性发生显著变化,0极点应当接近且接近原点,消除极点的影响 为什么需要接近原点:\(\beta\)不会小的,这样为了使0极点绝对接近,必须是二者都小,比如0.01和0.001,相对差距大,但是绝对差距小 这样一来闭环极点只会偏离一点,而\(|G_c(s)|\approx \hat{K}_c,\angle G_c(s)\in(-5^\circ, 0)\) 当\(\hat{K}_c\approx1\)时,瞬态响应不明显改变 校正后的系统的静态速度误差常数\(\hat{K}_v = \hat{K}_c\beta K_v\approx \beta K_v\),由指定的静态误差常数决定\(\beta\)的值 选取的\(T\)只需要满足0极点相近就行,没有特别的要求,根据幅值条件计算\(\hat{K}_c\) 可以加快响应,减小稳态误差;同时增加了瞬态和稳态性能 为系统串联 由于\(\angle \frac{s+1/T_2}{s+1/\beta T_2}\)很小,故可以通过辐角缺额确定\(\gamma,T_1\)的值,进而根据幅值条件确定\(K_c\)的值 串联上\(G_c\)后系统的静态速度误差常数\(K_v=\lim\limits_{s\rightarrow0}sG_cG=sK_c\frac{\beta}{\gamma}G\),根据要求的\(K_v\)值确定\(\beta\)的值,继而选择\(T_2\)的值 注意,\(\beta T_2\)不能太大,否则物理上无法实现 PI控制:\(G_c=k_p(1+\frac{1}{T_i s})\),\(z=-\frac{1}{T_i},p=0\),是一个滞后矫正器,提高了稳态特性 PD控制:\(G_c=k_p(1+T_ds)\),\(z=-\frac{1}{T_d}\),没有极点,是一个超前矫正器,提高了瞬态特性 PID控制:\(G_c=k_p(1+\frac{1}{T_i s}+T_ds)\),两个0点,一个极点,是一个滞后-超前矫正,但是相对于4点的矫正器又少一个参要调,更方便 控制器位于小回路,长这样 其中\(G_c(s)\)是矫正器,系统的闭环传递函数为4.2.4 确定出射角
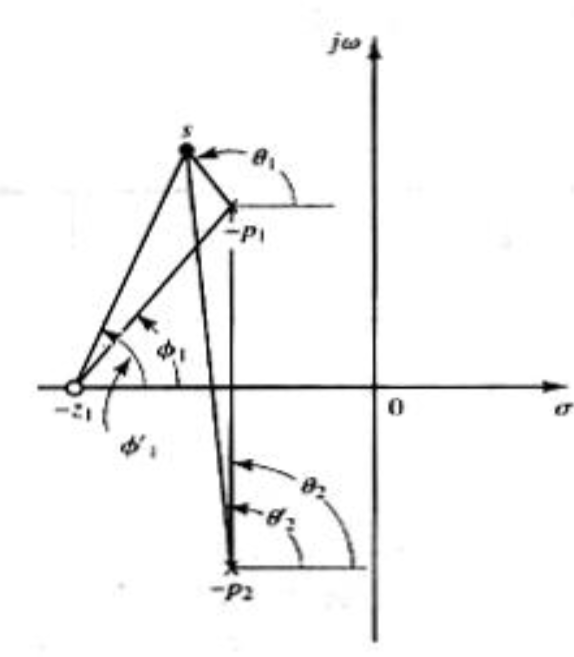
\[
\theta_1 = \pi - \theta_2 + \varphi_1
\]
根据对称性共轭极点的出射角相同,0点则是根轨迹终点,不需要求4.2.5 完整的根轨迹
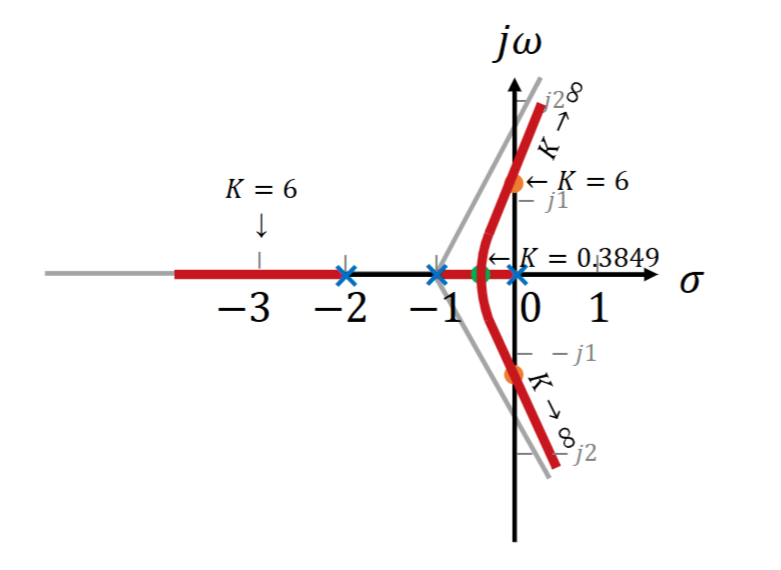
4.2.6 确定闭环主导极点
\[
K = \left| \frac{\Pi(s-p_i)}{\Pi(s-z_i)} \right|
\]
得到\(K = 1.0383\),利用K求得第三个极点\(s=-2.3326\),在图上表现为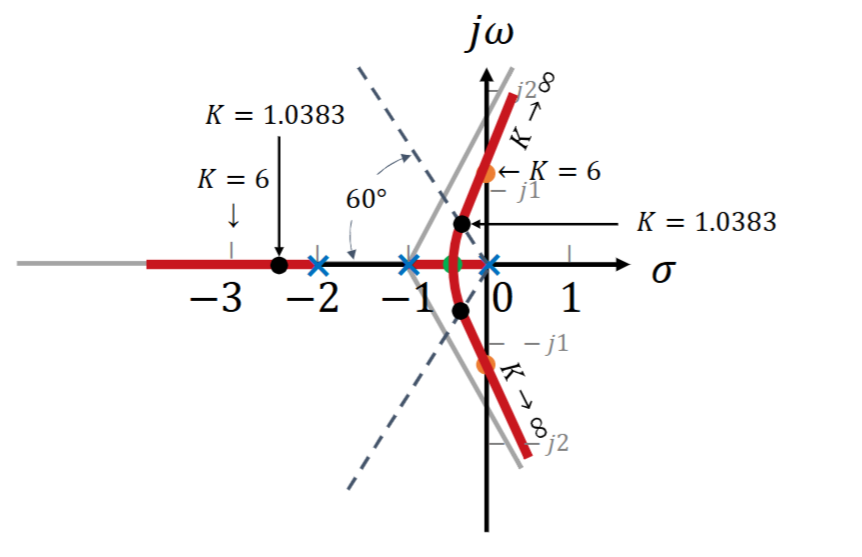
4.2.7 另一个例子
4.3 根轨迹图的说明
4.3.1 闭环极点的结论
\[
\underset{i=1}{\overset{n}{\Pi}}(s-p_i) + K\underset{i=1}{\overset{m}{\Pi}}(s-z_i) = \underset{i=1}{\overset{n}{\Pi}}(s-s_i) = s^n +a_1s^{n-1}+\ldots + a_{n-1}s+a_n
\]
其中\(s_i\)是闭环极点,有如下结论
\[
\underset{i=1}{\overset{n}{\Pi}}s_i = (-1)^n a_n\\
\underset{i=1}{\overset{n}{\sum}} s_i =-a_1
\]
当\(n-m\geq 2 \)时,
4.3.2 变量参数不以乘法因子出现
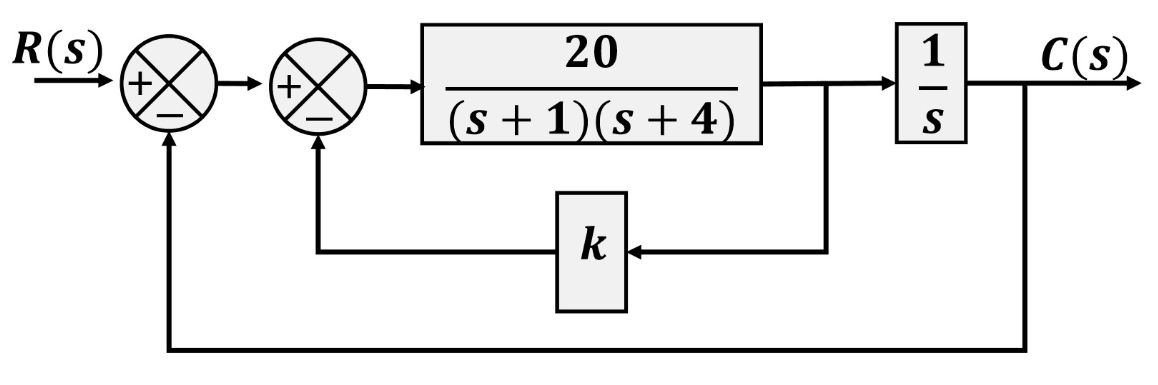
\[
1+\frac{20ks}{s(s+1)(s+4)+20}=0
\]
这就是标准的形式,\(K\triangleq 20k\),为增益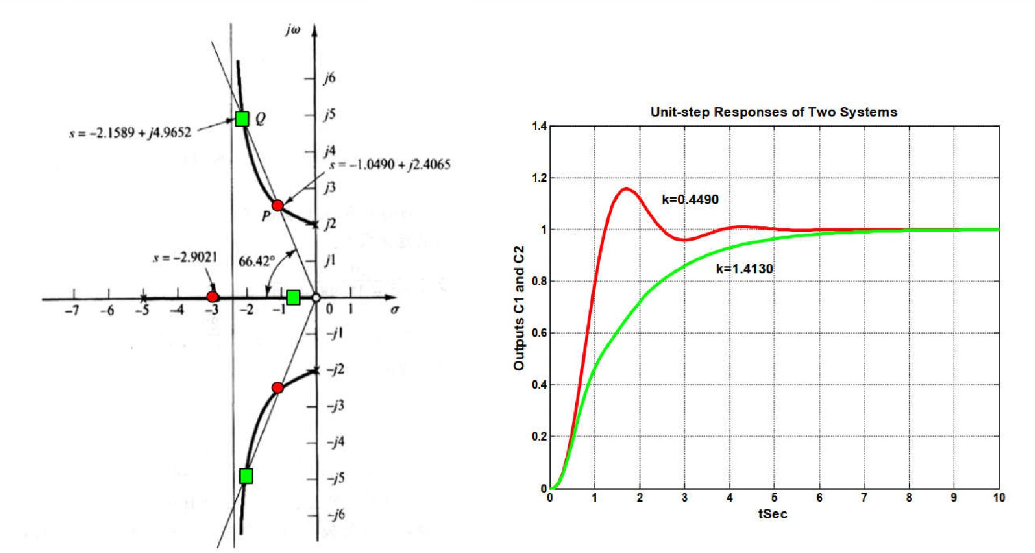
4.3.3 \(G,H\)的0极点相消
\[
1+\frac{K(s+1)}{s(s+1)(s+2)} = 0
\]
此时不能削去\(s+1\),很显然这是一个闭环极点4.3.4 非最小相位系统
\[
G(s) = \frac{K(1-T_as)}{s(Ts+1)}
\]
由于之前讨论的都是\(1+\frac{K\Pi(s-z_i)}{\Pi(s-p_i)}=0,K>0\)的形式,这里需要改写\(G(s)=-\frac{(T_as-1)}{s(Ts+1)}\)
\[
\angle\frac{K(T_a-1)}{s(Ts+1)} = 2k\pi
\]
对应的一些结论也要改变,不过不记结论就行4.3.5 正反馈系统
\[
1- GH=0
\]
同样也是辐角条件改变为
\[
\angle GH = 2k\pi
\]
4.3.6 条件稳定系统
4.3.7 具有传递延迟的系统的根轨迹
4.4 矫正系统
4.4.1 初步设计研究
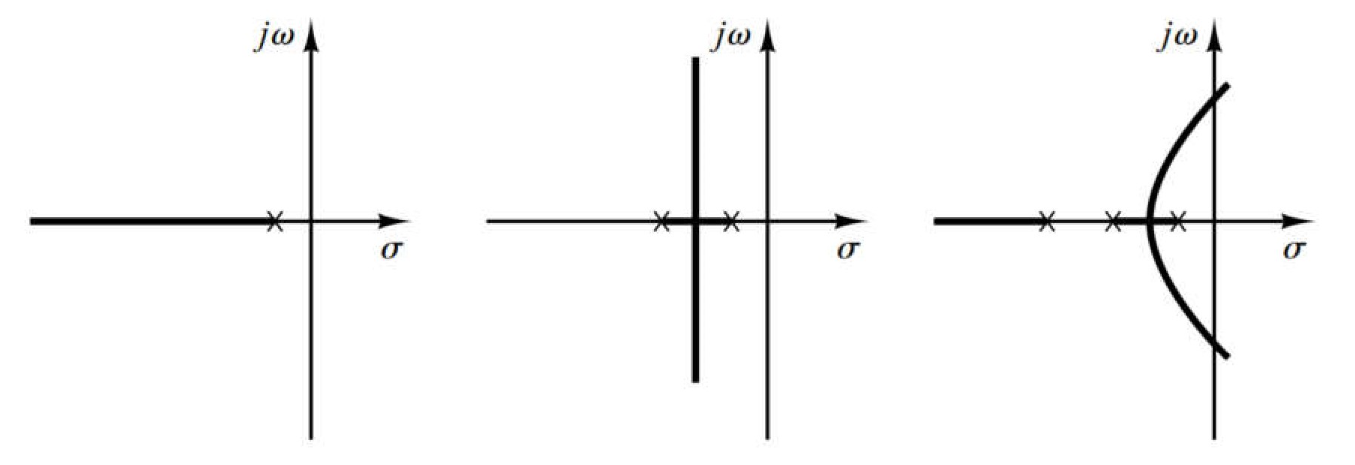
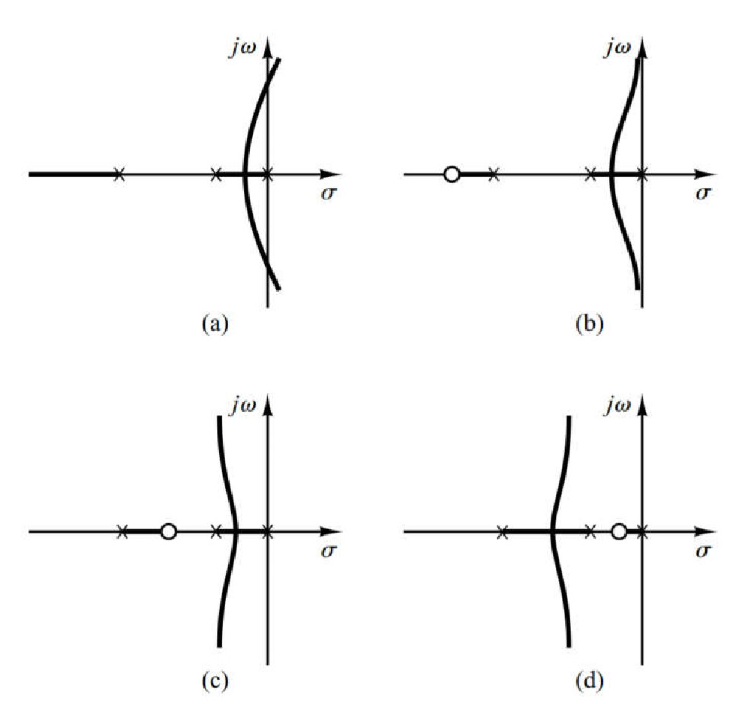
4.4.2 超前矫正
\[
G_c(s) = K_c \frac{s+\frac{1}{T}}{s+\frac{1}{\alpha T}}
\]
为了使得相位是正(超前),且系统稳定,有\(-\frac{1}{\alpha T}<-\frac{1}{T}\Rightarrow \alpha\in(0,1)\),\(\alpha,T\)的值由辐角缺额条件决定,而\(K_c\)由幅值条件确定4.4.3 滞后校正
\[
G_c(s)=\hat{K}_c\frac{s+\frac{1}{T}}{s+\frac{1}{\beta T}}
\]
其中\(\beta>1\)4.4.4 滞后-超前矫正
\[
G_c(s)=K_c\frac{s+\frac{1}{T_1}}{s+\frac{\gamma}{T_1}}\cdot\frac{s+\frac{1}{T_2}}{s+\frac{1}{\beta T_2}}
\]
其中\(\beta>1,\gamma=\frac{1}{\alpha}>1\),为了方便\(\beta=\gamma\),故取倒数4.4.5 并联矫正
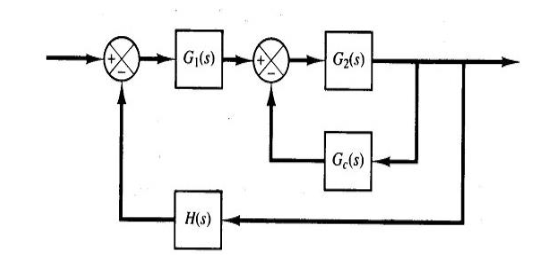
\[
\frac{C}{R}=\frac{G_1G_2}{1+G_2G_c+G_1G_2H}
\]
特征方程是\(1+G_2G_c+G_1G_2H=0\),不是标准形式,将不包含\(G_c\)的项除去,得到
\[
1+\frac{G_2G_c}{1+G_1G_2H}=0
\]
定义\(G_f=\frac{G_2}{1+G_1G_2H}\),则特征方程为
\[
1+G_cG_f=0
\]