3 瞬态响应和稳态响应分析
3.1 相关概念
在系统一段加入信号\(r(t)\)后,得到输出\(c(t)\),将其分为\(c(t)=c_t(t)+c_s(t)\),分别时瞬态和稳态响应
\(c_t(t)\)满足\(\lim\limits_{t\rightarrow\infty}c_t(t)=0\)
对线性系统而言,\(r(t)\)只影响\(c_s(t)\),因为\(c_t(t)\)在无穷时刻恒为0
稳定性
绝对稳定性:指系统的稳定性,分为稳定,临界稳定,不稳定,分别表示稳定,周期振荡和不稳定的输出
相对稳定性:指在一个裕度内系统稳定,瞬态指标
稳态误差:达到稳态响应后,系统输出与预期值的误差,即\(e_{ss}=\lim\limits_{s\rightarrow0}sE(s)=s\cdot(X-HY)=\frac{sX}{1+GH}\)
3.2 一阶系统
讨论传递函数为\(\frac{C}{R}=G(s)=\frac{1}{Ts+1}\)的系统
3.1.1 单位阶跃响应
\(r(t)=u(t)\Rightarrow R(s)=\frac{1}{s}\),得到\(c(t)=1-e^{-\frac{t}{T}}\),其中\(c_t(t)=-e^{-\frac{t}{T}},c_s(t)=1\),误差\(e(t)=e^{-\frac{t}{T}}\)
稳态误差=0
在\(t=4T\)时,系统达到98.2%稳定值,此时认为系统稳定,4T为响应时间
3.1.2 单位斜坡响应
\(r(t)=tu(t)\Rightarrow R(s)=\frac{1}{s^2}\),得到\(c(t)=t-T+Te^{-\frac{t}{T}}\),\(e(t)=r(t)-c(t)=T(1-e^{-t/T})\)
稳态误差=T,响应时间4T
3.1.3 单位脉冲响应
\(r(t)=\delta(t)\Rightarrow R(s)=1\),得到\(c(t)=\frac{1}{T}e^{-\frac{t}{T}}\),\(e(t)=r(t)-c(t)=\delta(t)-\frac{1}{T}e^{-\frac{t}{T}}\)
稳态误差=0,响应时间4T
3.1.4 LTI系统特征
其实就是能用卷积表达输出,最终得到\(x^{(n)}*h=(x*h)^{(n)}=y^{(n)}\)
3.3 二阶系统
讨论伺服系统(精确跟随或复现某个过程的反馈系统)
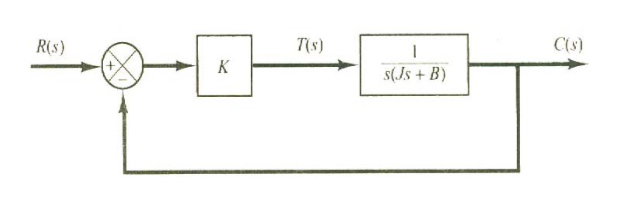
系统传递函数\(G(s)=\frac{K}{Js^2+Bs+K}=\frac{K/J}{[s+\frac{B}{2J}+\sqrt{(\frac{B}{2J})^2-\frac{K}{J}}][s+\frac{B}{2J}-\sqrt{(\frac{B}{2J})^2-\frac{K}{J}}]}\)
令\(\frac{K}{J}=\omega_n^2,\frac{B}{J}=2\zeta\omega_n=2\sigma\),其中σ是衰减系数,\(\omega_n\)为无阻尼自然频率,\(\zeta\)是系统的阻尼比
\(\zeta=\frac{B}{B_c}\),其中\(B,B_c\)分别为实际阻尼、临界阻尼系数,\(B_c\)是\((\frac{B}{2J})^2-\frac{K}{J}=0\)的解,故\(\zeta=\frac{B}{2\sqrt{JK}}\)
传递函数可以改写为\(G(s)=\frac{\omega_n^2}{s^2+2\zeta\omega_ns+\omega_n^2}\),极点为\(s_{1,2}=-\zeta\omega_n\pm j\omega_n\sqrt{1-\zeta^2}=-\sigma \pm j\omega_d\),\(|s_{1,2}|=\omega_n\)
记\(\omega_d=\omega_n\sqrt{1-\zeta^2}\)为阻尼自然频率,可观察到的总是\(\omega_d\),总是小于\(\omega_n\)
对\(\zeta\)做以下讨论:
- \(0<\zeta<1\),欠阻尼,瞬态响应是振荡的
- \(\zeta=1\),临界阻尼,瞬态响应不振荡
- \(\zeta>1\),过阻尼,瞬态响应不振荡
- \(\zeta=0\),无阻尼,瞬态响应为正弦振荡(等幅)
单位阶跃响应
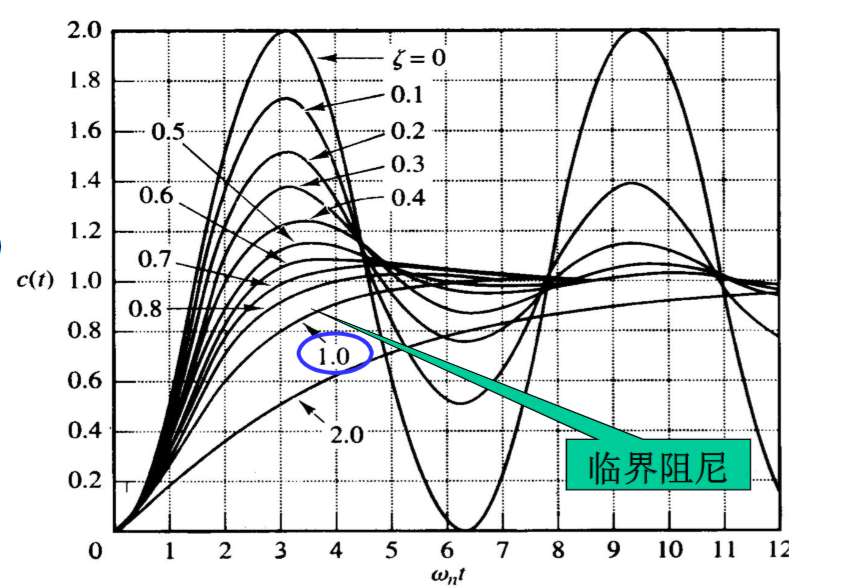
上图为不同阻尼比下的响应
在\(\zeta>0\)时,稳态误差总是0
在\(\zeta=1\)时,两个极点重合,\(c(t)=1-e^{-\omega_nt}(1+\omega_nt)\)
实际上,在两个极点接近相等时,系统也可以近似看为临界阻尼
在\(\zeta>>1\)时,\(s_{1,2}=(-\zeta\pm \sqrt{\zeta^2-1})\omega_n\),在频率不大的情况下,\(s_2\)对系统的影响很小,可忽略(\(e^{-\infty t}\),那么\(t\)对结果就没有影响)
\(c(t)\approx 1-e^{(-\zeta+\sqrt{\zeta^2-1})\omega_nt}\)
由上图可知,当\(0.4<\zeta<0.8\)时,其响应曲线比临界阻尼或过阻尼系统更快达到稳定值
且在无震荡系统中,临界阻尼有最快响应特性;而过阻尼系统对任何输入信号的响应都是缓慢的
3.4 瞬态响应指标
都是在0状态下的指标
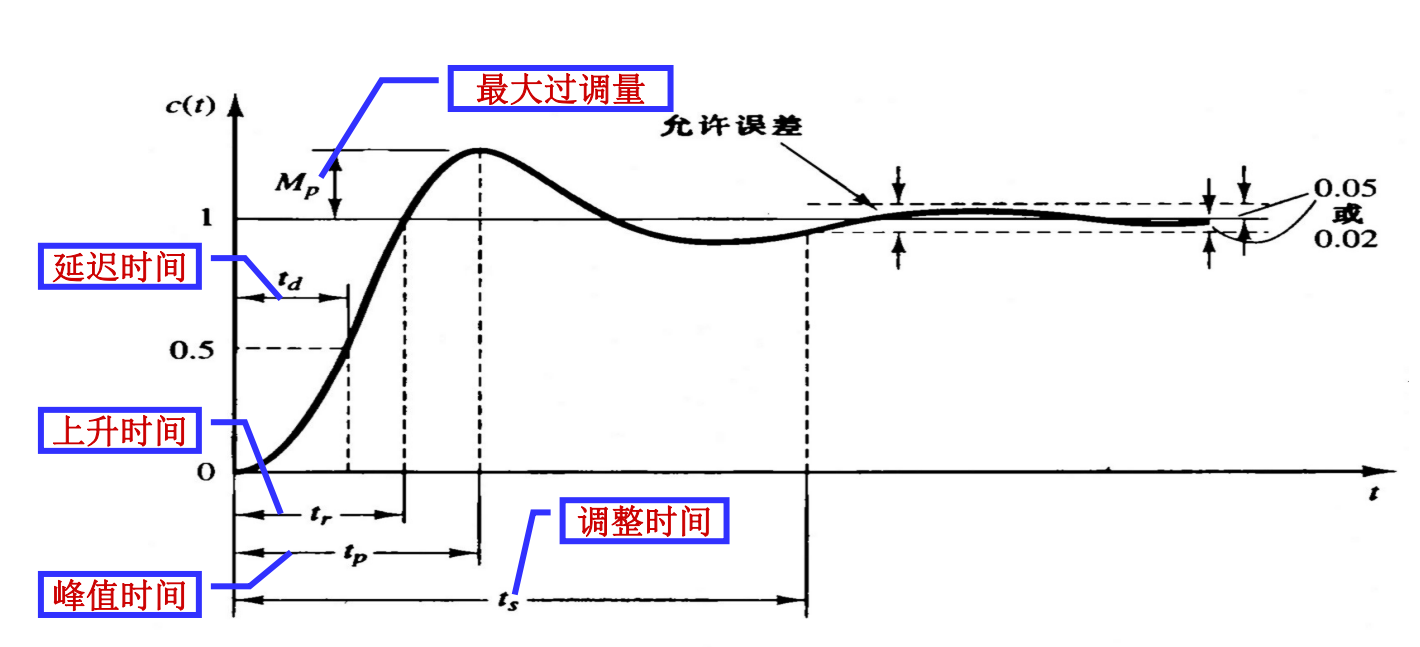
延迟时间\(t_d\):第一次到达稳态值一半所需的时间
上升时间\(t_r\):从稳态值的0%到100%所需要的时间
峰值时间\(t_p\):到达过调量的第一个峰值所需的时间
最大过调量\(M_p\):计算公式为\(M_p=\frac{最大峰值-c(\infty)}{c(\infty)}\times100\%\),直接说明了系统的相对稳定性
调整时间\(t_s\):用一个稳态值的百分比误差范围,曲线达到并永远保持在这个范围内所需的时间,与系统的最大时间常数有关(如一阶系统的4T)
很显然,最大过调量和上升时间是相互矛盾的,必须做一个取舍
3.4.1 二阶系统的瞬态响应指标
注意,以下所讲的都是对于二阶系统的阶跃响应而言
\[
c(t)=1-e^{-\zeta\omega_n t}\left( \cos{\omega_d t}+\frac{\zeta}{\sqrt{1-\zeta^2}}\sin{\omega_d t}\right)
\]
上升时间
当\(c(t)=1\)时,解得
\[
t_r=\frac{1}{\omega_d}\tan^{-1}{\frac{\omega_d}{-\sigma}}=\frac{\pi - \beta}{\omega_d}
\]
其中\(\beta\)如图
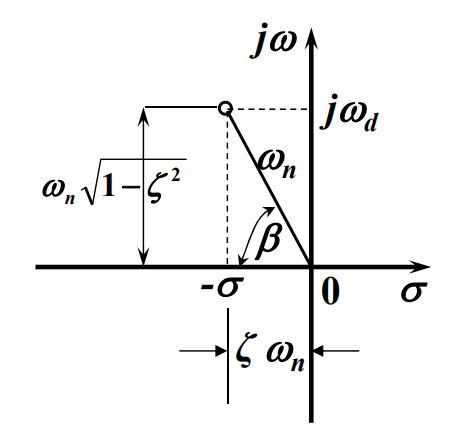
峰值时间
当\(\frac{dc(t)}{dt}=0\)时就是峰值时间
\[
\sin{\omega_d t_p}=0\Rightarrow t_p = \frac{k\pi}{\omega_d}
\]
由于是第一个,\(t_p=\frac{\pi}{\omega_d}\),是阻尼振荡周期的一半
最大过调量
显然发生在\(t_p\)上 衰减比 同方向的两个相邻波峰的比值,此处为\(M(t_{p1})/M(t_{p3})\),是减去了稳态输出的 可见如果两个二阶系统用同样的ζ,它们就会出现相同的过调量和震荡模式,这类系统称为具有相同相对稳定性的系统 调整时间 对于欠阻尼二阶系统,其响应被两条曲线包围,分别是\(1\pm (e^{-\zeta\omega_n t}/\sqrt{1-\zeta^2})\),这条曲线的时间常数是\(1/\zeta\omega_n\) 对于闭环传递函数 \[
{C(s)} = \frac{a}{s}+\sum\frac{a_i}{s+p_i}
\] 其中\(a_i=(s+p_i)\frac{C(s)}{R(s)}|_{s=-p_i}\),是\(s=-p_i\)这个极点的留数(默认都是一阶的) 做几个讨论: \[
C(t) = a + \sum a_ie^{-p_it}+\sum b_ke^{-\zeta_k\omega_kt}\cos{(\omega_k\sqrt{1-\zeta^2}t)}+\sum b_ke^{-\zeta_k\omega_kt}\sin{(\omega_k\sqrt{1-\zeta^2}t)}
\] 稳定的高阶系统响应曲线是一些指数曲线和阻尼正弦曲线之和 如果所有的极点都在左半平面,那么系统最终的稳定输出为\(a\) 做几个讨论: 在上述区域中,系统的稳定性最好 但是,即使系统稳定,也不能保证有满意的瞬态响应特性 写出系统(闭环传递函数)的特征方程 系统稳定的必要条件:所有系数都是正数。即有负的系数那么一定不稳定 若所有系数都是正数,按以下方式列数(没有就用0补齐) 其中\(b_1=\frac{a_1a_2-a_0a_3}{a_1}, b_2=\frac{a_1a_4-a_0a_5}{a_1}, c_1=\frac{b_1a_3-a_1b_2}{b_1}\),依次类推 计算系数必须算到全为零位置(就是一列连续出现两个0,那么下一行的某个值一定是0) 整个阵列可以用正数乘/除一整行,结论不变 劳斯稳定判据:特征方程中具有的正实部的根的数目,等于阵列的第一列的系数符号改变次数 稳定的充要条件 方程的全部系数都是正值,且第一列所有系数都是正号 例:单位负反馈系统的前向传递函数为\(\frac{K}{s(s+1)(s+2)}\),求系统稳定的K的范围 解:系统的闭环传递函数为\(\frac{K}{s^3+3s^2+2s+K}\),特征方程为\(s^3+3s^2+2s+K=0\),列出阵列为 要使系统稳定,那么\(0 第一列存在0 用一个很小的正数\(\varepsilon\)来代替0,继续进行阵列计算 如果0上下的系数符号相同,那么系统存在一对虚根;如果不同,系统存在一个符号变化 前者说明系统临界稳定;后者说明系统不稳定 某一行的所有系数都是0 表明系统存在一对奇对称的根 可以构造辅助多项式,如 将全0行的上一行用来构造辅助多项式 存在一个正实部的根,不稳定 劳斯判据是将特征根与0比,得出系统的绝对稳定性 令\(s = \hat{s}-\sigma\),带入特征方程,重写对于\(\hat{s}\)的阵列,将\(\hat{s}\)与0对比,就可以判断系统在\(-\sigma\)右侧的根的个数 对于阶跃信号,没有积分器时,系统的比例控制会造成稳态误差 这里的没有积分器指的是反馈环节没有积分器 控制器存在积分环节,可消除误差 单位阶跃的稳态误差是 系统的阻尼比为 绝对不能单独使用,因为微分是非因果的,它在预测 优点:能反映误差信号的变化速度,在误差变大前修正,提高系统稳定性;增加了系统的阻尼,允许更大的增益K,改善精度 依照开环传递函数对系统进行分类,单位反馈的意思是反馈是\(H(s) = 1\) 一切的前提是单位反馈 是系统对单位阶跃信号的特性 系统的稳定误差为\(e = \frac{1}{1+G(0)}\),定义\(K_p = \lim\limits_{s\rightarrow 0}G(s)\),\(e=\frac{1}{1+K_p}\) 对于0型系统,\(K_p = K\) 对于1型或更高系统,\(K_p = \infty\),此时稳态误差为0 是系统对单位斜坡信号的特性 系统的稳定误差为\(e = \frac{s}{(1+G(s))s^2}=\lim\limits_{s\rightarrow 0}\frac{1}{sG(s)}\),定义\(K_v = \lim\limits_{s\rightarrow 0}sG(s)\),\(e = \frac{1}{K_v}\) 对于0型系统,\(K_v = 0\) 对于1型系统,\(K_v = K\) 对于2型或更高系统,\(K_v =\infty\),此时稳态误差为0 是系统对单位抛物线信号的特性,单位抛物线信号为\(r(t) = \frac{t^2}{2},t>0\) 系统的稳态误差为\(e =\lim\limits_{s\rightarrow 0}\frac{1}{s^2G(s)}\),定义\(K_a=\lim\limits_{s\rightarrow 0}s^2G(s)\),\(e = \frac{1}{K_a}\) 对于0型和1型系统,\(K_a = 0\) 对于2型系统,\(K_a = K\) 对于3型或更高系统,\(K_a = \infty\) 误差常数越大,系统的误差越小 故为了满足系统的响应条件,可以增大误差常数 如果\(K_v\)和\(K_a\)存在矛盾,应该先满足前者 系统更高阶就是积分器更多,增加积分器可以更稳定,但是很难设计
\[
M_p = \left(c(t_p)-1\right)/1=e^{-\frac{\sigma}{\omega_d}\cdot \pi}\times 100\%
\]
如果阻尼比\(0.4<\zeta<0.8\),那么\(2.5\%
\[
n=e^{2\pi {\zeta}/{\sqrt{1-\zeta^2}}}
\]
\[
t_s = 4T = \frac{4}{\zeta \omega_n} \,\,\,\,\,\,\,\,2\% 误差标准\\
t_s = 3T = \frac{3}{\zeta \omega_n} \,\,\,\,\,\,\,\,5\% 误差标准
\]3.5 高阶系统的瞬态响应
\[
\frac{C(s)}{R(s)}=k\frac{\Pi (s+z_i)}{\Pi(s+p_j)}
\]
对于单位阶跃信号的响应可以化为3.5.1 闭环极点均为不同的实数
3.5.2 闭环极点由实数极点和成对的共轭复数极点组成
3.5.3 闭环主导极点
3.5.4 复平面上的稳定性分析
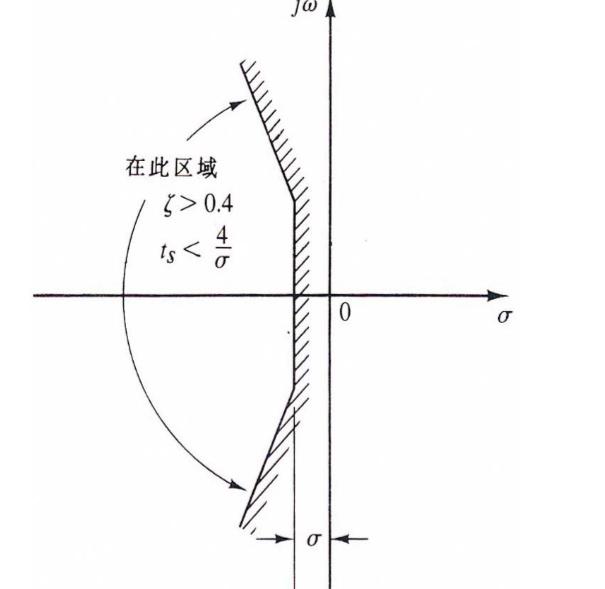
3.6 劳斯稳定判据
3.6.1 应用步骤
\[
a_0s^n+a_1s^{n-1}+\ldots+a_{n-1}s+a_0 = 0
\]
其中\(a_0\neq0\),排除所有0根
s
k1
k2
k3
k4
...
\(s^n\)
\(a_0\)
\(a_2\)
\(a_4\)
\(a_6\)
...
\(s^{n-1}\)
\(a_1\)
\(a_3\)
\(a_5\)
\(a_7\)
...
\(s^{n-2}\)
\(b_1\)
\(b_2\)
\(b_3\)
\(b_4\)
...
\(s^{n-3}\)
\(c_1\)
\(c_2\)
\(c_3\)
\(c_4\)
...
...
...
...
...
...
...
\(s^2\)
\(d_1\)
\(d_2\)
\(d_3\)
0
0
\(s\)
\(e_1\)
\(e_2\)
0
0
0
\(s^0\)
\(f_1\)
0
0
0
0
s
K1
k2
s^3
1
2
s^2
3
K
s^1
\(\frac{6-K}{3}\)
0
s^0
K
0
3.6.2 特殊情况
\[
s^5+2s^4+24s^3+48s^2-25s-50=0
\]
s
K1
k2
k3
s^5
1
24
-25
s^4
2
48
-50
s^3
0
0
0
s^2
s^1
s^0
\[
2s^4+48s^2-50=0
\]
由于这是高一次的多项式,对这个多项式求导得到\(s^3\)的多项式
\[
8s^3+96s=0
\]
按这个系数代替全0行
s
K1
k2
k3
s^5
1
24
-25
s^4
2
48
-50
s^3
8
96
0
s^2
24
-50
0
s^1
112.7
0
0
s^0
-50
0
0
3.6.3 相对稳定性分析
3.7 积分和微分控制作用对系统性能的影响
3.7.1 比例控制
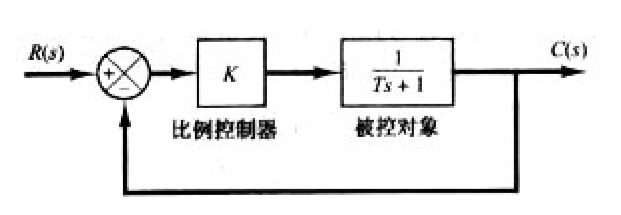
\[
E/R = (R-C)/R = 1-C/R=\frac{1}{1+G(s)}\\
G(s)=\frac{K}{Ts+1}
\]
得到稳态误差
\[
E = \frac{Ts+1}{Ts+1+k}\frac{1}{s}\\
e(\infty) = \lim\limits_{s\rightarrow0}sE(s)=\frac{1}{K+1}
\]3.7.2 积分控制
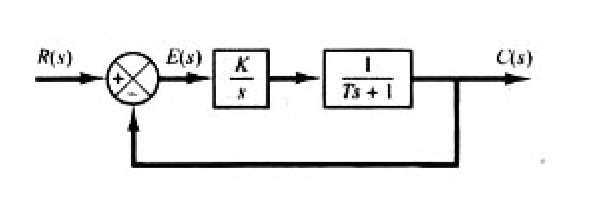
\[
e_s = \lim\limits_{s\rightarrow 0}sE(s)=\lim\limits_{s\rightarrow 0}\frac{s^2(Ts+1)}{Ts^2+s+K}\cdot \frac{1}{s}=0
\]
但是积分控制也使得输出振荡,不太好3.7.3 微分控制
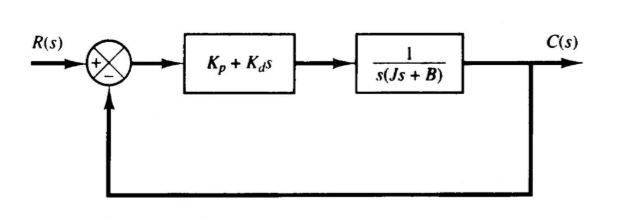
\[
\zeta = \frac{B+K_d}{2\sqrt{K_pJ}}
\]3.8 单位反馈控制系统的稳态误差
\[
G(s) = \frac{K\cdot\Pi(T_i s+1)}{s^N\cdot \Pi (T_js+1)}
\]
对纯积分环节数进行分类,也就是上式的\(N\)3.8.1 稳态误差
\[
\frac{E}{R} = \frac{R-C}{R} = 1-\frac{G}{1+G} =\frac{1}{1+G}\\
E(s) = R(s)\frac{1}{1+G}\\
e(\infty) = \lim\limits_{s\rightarrow 0}sE(s) = \lim\limits_{s\rightarrow 0}\frac{sR(s)}{1+G(s)}
\]3.8.2 静态位置误差常数\(K_p\)
3.8.3 静态速度误差常数\(K_v\)
3.8.4 静态加速度误差常数\(K_a\)
3.8.5 小结