2 控制系统的数学模型
建立方法:
- 解析法。依据数理规律建立准确模型
- 实验法。把系统当黑箱,也称系统辨识
2.1 数学模型的分类
线性/非线性,分布性/集总性(能否用有限原件描述),参数时变性
只考虑线性时不变集总模型,用线性常微分方程描述
方程的输出阶次大于输入阶次,否则会有不因果
2.2 传递函数和脉冲响应
在全部初始条件为0的假设下,传递函数\(H(s)=\frac{Y(s)}{X(s)}\)
称\(X(s)=0\)为系统的特征方程,\(X(s)\)的最高阶次为系统的阶次
s=0时,\(H(0)\)的值是系统的放大系数/增益,表示系统处于静态时输出与输入之比
这里有必要说明:\(X(s)=0\)指的就是传递函数的极点,这种表述在定义上不准确,但是在数学上是等价的
说明:
- H(s)仅取决于系统,与输入无关
- H(s)不提供系统的物理结构的信息
- 当H(s)已知时,系统的动态特性被充分的描述
- h(t)称为系统的权函数,是初始条件全部为零时得到的
- 当系统的时间常数较大时,很短的脉动信号可以视为脉冲信号
2.3 自动控制系统
2.3.1 方框图
各个元件的功能和信号回流的图解表示,表示各种元件之间的互相关系
闭环系统框图
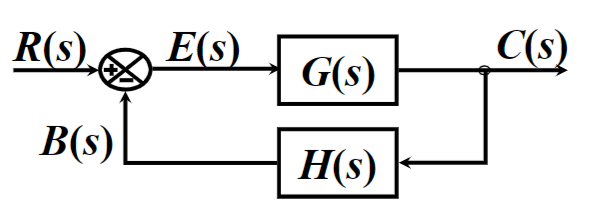
定义:\(开环传递函数=\frac{反馈信号}{误差信号} , 前向传递函数=\frac{输出量}{误差信号}\)
有\(开环传递函数=\frac{B(s)}{E(s)}=\frac{E(s)G(s)H(s)}{E(s)}=G(s)H(s),前向传递函数=\frac{C(s)}{E(s)}=\frac{E(s)G(s)}{E(s)}=G(s)\)
\(闭环传递函数=\frac{输出量}{出入量}=\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)H(s)}\)
2.3.2 扰动下的闭环系统
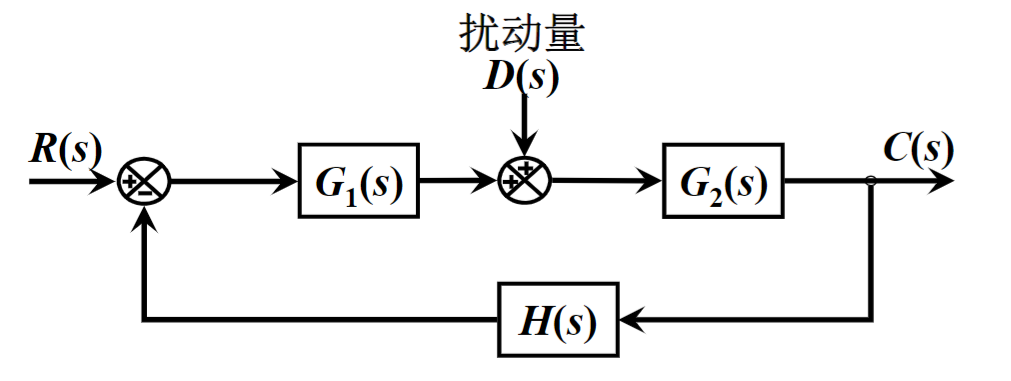
扰动也是输入量,由于是LTI系统,可以将R(s)与D(s)单独作用后叠加
扰动的闭环传递函数=\(\frac{G_2}{1+G_2\cdot G_1H}\),可以将扰动视为以G2为增益,以HG1为反馈的系统
激励的闭环传递函数=\(\frac{G_1G_2}{1+G_1G_2\cdot H}\)
系统的闭环传递函数为二者相加,在\(|G_1G_2H|>>1\)时,扰动的干扰很小
2.3.3 自动控制器
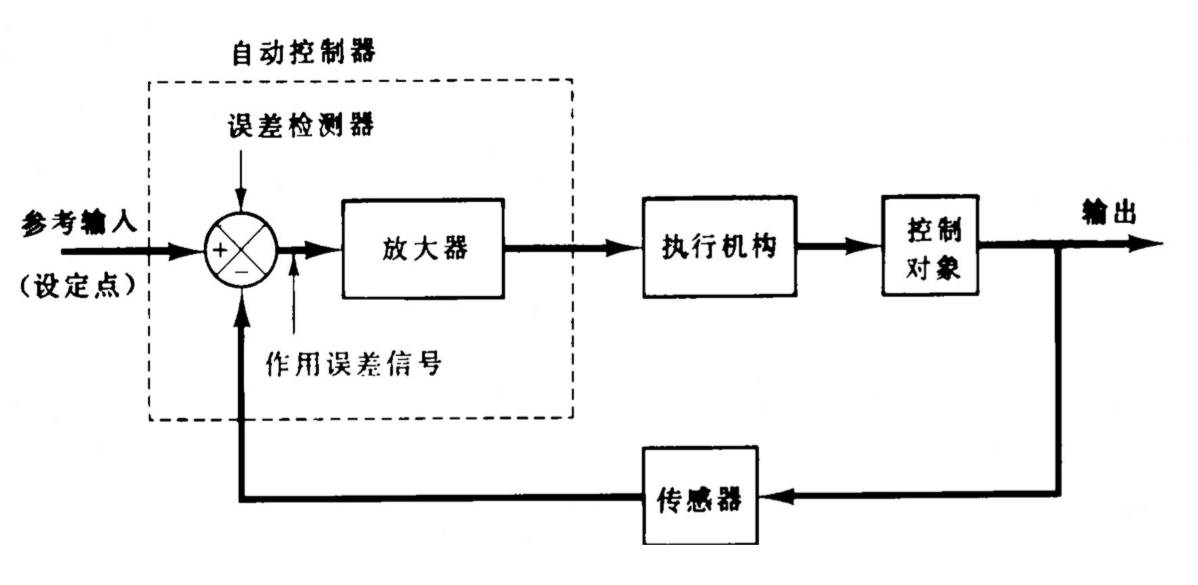
2.4 工业控制器分类
2.4.1 双位/开关控制
\[
u(t)=\begin{cases}
U_1,\,\, e(t)>0\\
U_2,\,\, e(t)<0\\
\end{cases}
\]
其中e(t)为误差
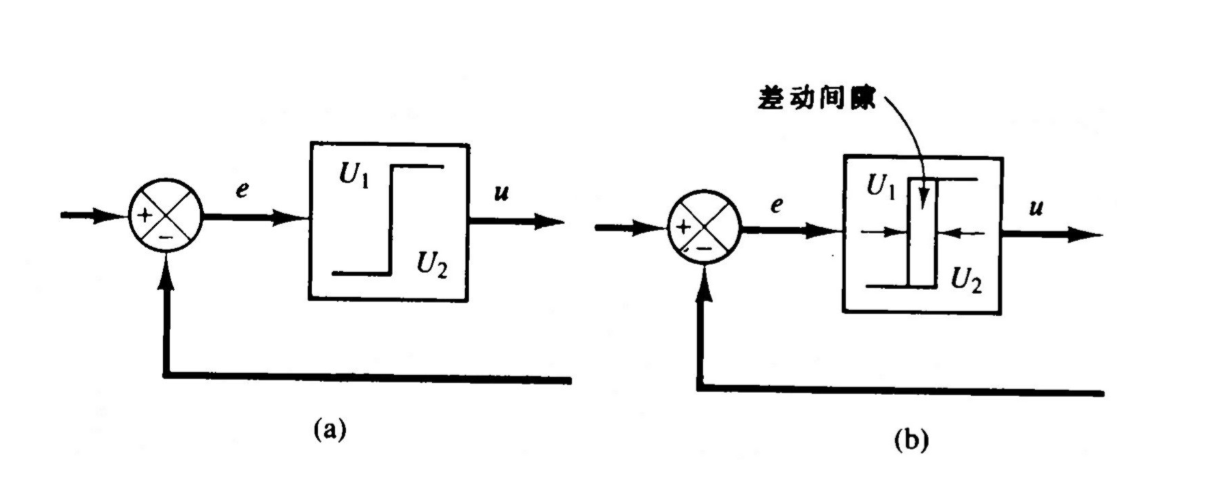
2.4.2 比例控制
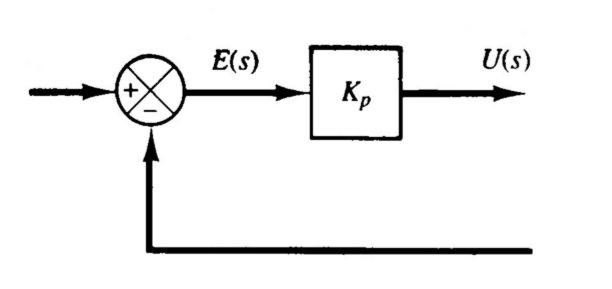
\[ u(t)=K_pe(t) \]
比例增益为\(\frac{U(s)}{E(s)}=K_p\)
2.4.3 积分控制
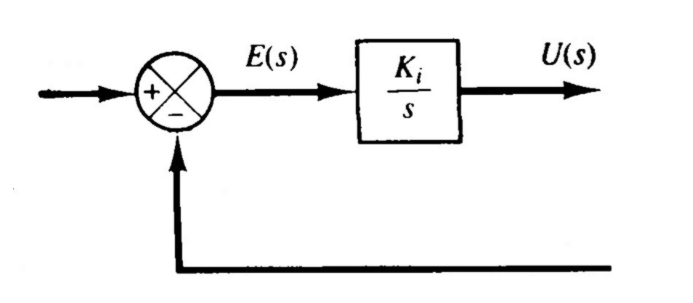
\[ u(t)=K_i\int_0^t e(a)da \]
积分增益为\(\frac{U(s)}{E(s)}=\frac{K_i}{s}\)
2.4.4 比例积分控制
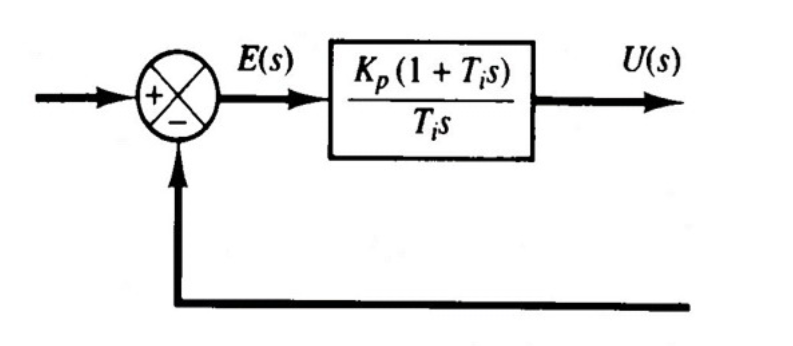
\[ u(t)=K_pe(t)+\frac{K_p}{T_i}\int_0^te(a)da \]
其中\(T_i\)为积分时间常数,PI增益为\(\frac{U(s)}{E(s)}=K_p(1+\frac{1}{T_is})\)
2.4.5 比例微分控制
由于微分的非因果性,PD控制一定程度上可以预测误差
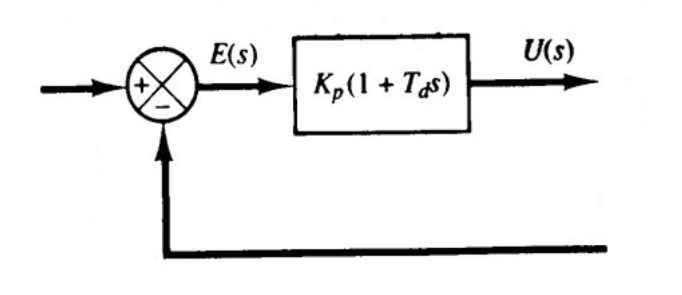
\[ u(t)=K_pe(t)+K_pT_d\frac{de(t)}{dt} \]
其中\(T_d\)为微分时间常数,PD增益为\(\frac{U(s)}{E(s)}=K_p(1+T_ds)\)
2.4.6 比例积分微分控制
比较难调
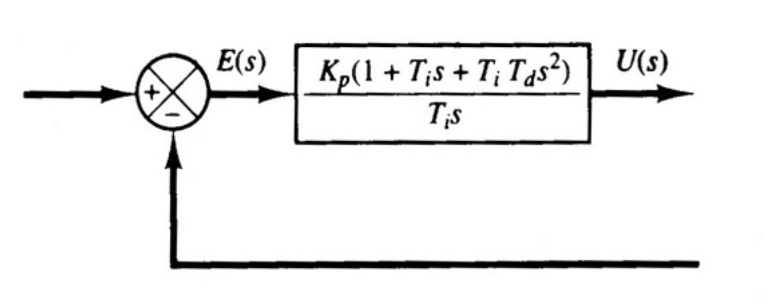
\[ u(t)=K_pe(t)+\frac{K_p}{T_i}\int_0^t e(a)da+K_pT_d\frac{de(t)}{dt} \]
PID增益为\(\frac{U(s)}{E(s)}=K_p(1+\frac{1}{T_is}+T_ds)\)
2.5 方框图的简化
原则
- 前向通路中传递函数的乘积不变
- 反馈回路中传递函数的乘积不变
2.5.1 代数法则简化
利用传递函数在频域的代数法则进行化简
例:化简并求总体传递函数C/R
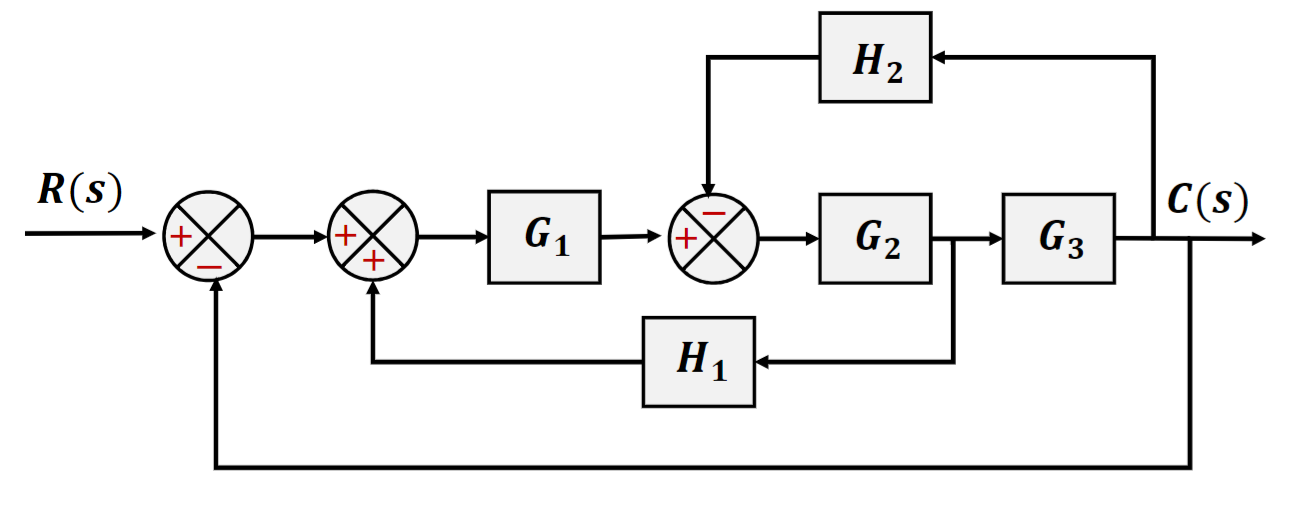
有兴趣就画吧,这种方法比较麻烦,结果是\(\frac{G_1G_2G_3}{1-G_1G_2H_1+G_2G_3H_2+G_1G_2G_3}\)
2.5.2 代数法求传递函数
将中间变量用输入量表示,比较麻烦
例:化简并求总体传递函数
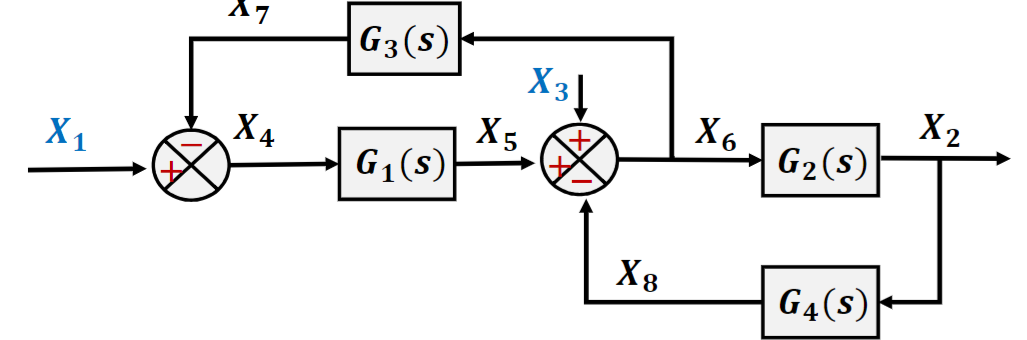
结果是\(X_2=\frac{G_1G_2}{1+G_1G_3+G_2G_4}X_1+\frac{G_2}{1+G_1G_3+G_2G_4}X_3\)
2.5.3 梅逊公式
当方框图有多个前向通路,且存在不接触的回路时,系统的总体传递函数C/R有
\[
\frac{C}{R}=\frac{1}{\Delta}\sum\limits_{k=1}^n {P_k\Delta_k}
\]
其中\(\Delta =1-\sum L_{(1)}+\sum L_{(2)}+\ldots+(-1)^m\sum L_{(m)}\)
\(\sum L_{(1)}\)是所有不同回路的传递函数之和(正负反馈的符号要注意)
\(\sum L_{(2)}\)是两两不接触的回路传递函数乘积之和,依次类推
\(P_k\)是第k条前向通路
\(\Delta_k\)是第k条前向通路的余因子,由\(\Delta\)将所有与这条通路接触的回路置零得到
对余因子的理解:重点在“余”,也就是必须包含前向通路没有的信息,舍弃所有已知信息,那么无论\(L_{(i)}\),只要其中一个回路接触了这个通路,就令\(L_{(i)}=0\)
例子可以拿前面两个练手,下面也给一个
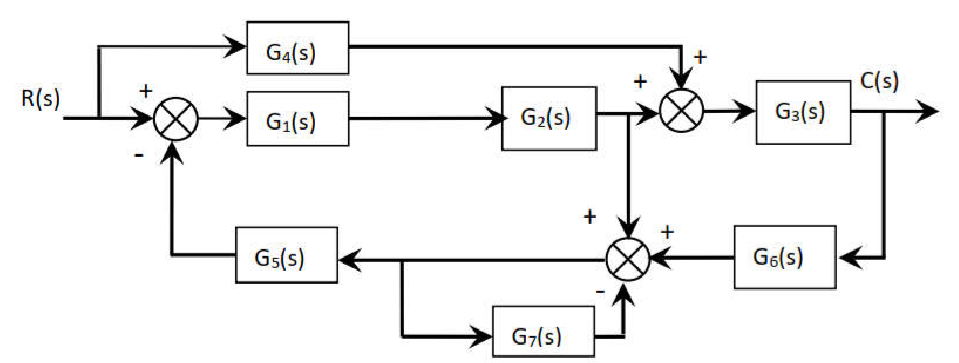
P1=G1G2G3, P2=G4G3
L1=-G1G2G5, L2=-G1G2G3G6G5, L3=-G7
为什么G3G5不是?因为箭头不构成回路; 为什么G4G3G6G5不是?因为G5不能回到G4
L(1)=L1+L2+L3, L(2)=0,都是有接触的
Δ=1-L(1), Δ1=1+G7, Δ2=1+G1G2G5+G7
C/R=(P1Δ1+P2Δ2)/Δ
另一个例子:
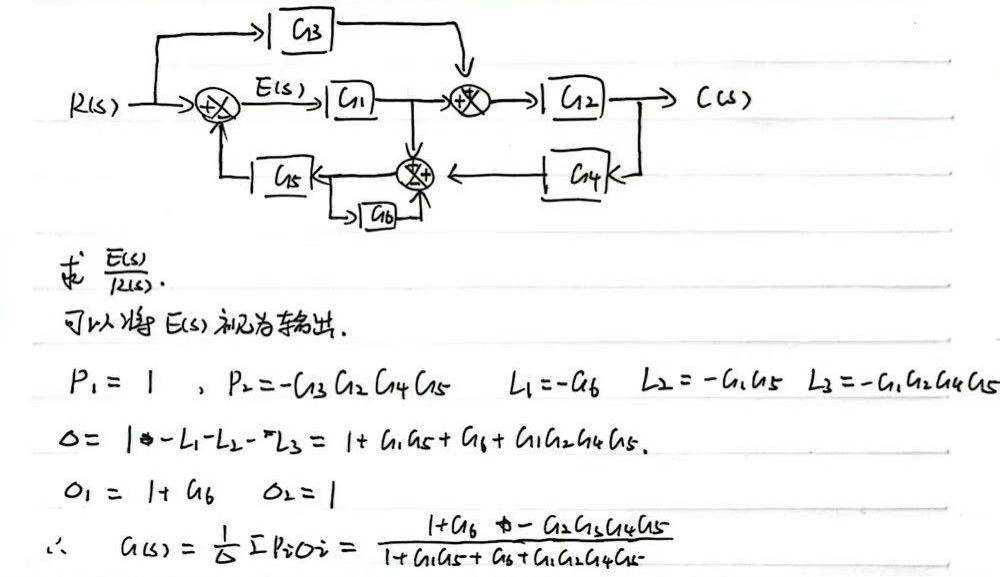
2.6 状态空间模型
多输入多输出模型,无论线性和时变性,任何系统都行,能在时域和频域建模
2.6.1 基本概念
状态:一组最小变量,能确定系统
状态变量:确定动态系统的状态
状态向量:将状态变量写成向量形式
状态空间:状态向量组成的空间
对于连续时间控制系统,积分器是记忆元件,其数目等于状态变量数目
2.6.2 状态空间方程
设系统的状态变量是\(x_i\),输入量是\(u_i\),输出量是\(y_i\)
有\(x(t)=[x_1(t),x_2(t),\ldots,x_n(t)]^\top\),y(t),u(t)同理,组成向量,得到方程
\[
\dot{x}(t)=f(x,u,t);y(t)=g(x,u,t)
\]
这是矩阵运算,对方程线性化为状态方程和输出方程
\[
\dot{x}(t)=A(t)x(t)+B(t)u(t)\,\,\,\,\,\,\,y(t)=C(t)x(t)+D(t)u(t)
\]
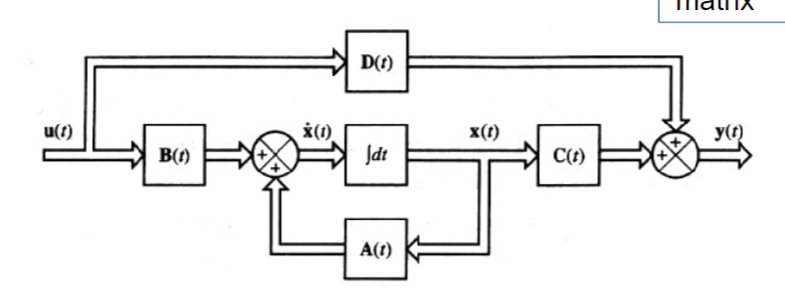
例:已知系统方程为\(m\ddot{y}+B\dot{y}+Ky=u\),求状态方程
解:有二阶导,显然需要2次积分,故状态变量为2个,令\(x_1=y,x_2=\dot{y}\),因为还要求导,所以这么设
则有\(\dot{x_1}=\dot{y}=x_2,\dot{x_2}=\ddot{y}=-\frac{K}{m}x_1-\frac{B}{m}x_2+\frac{1}{m}u,y=x_1\)
得到\(A=\left(\begin{matrix} 0 & 1\\ -\frac{K}{m} & -\frac{B}{m} \end{matrix}\right),B=\left(\begin{matrix} 0 \\ \frac{1}{m} \end{matrix}\right),C=\left(\begin{matrix} 1 & 0\end{matrix}\right),D=0\)
2.6.3 传递函数和状态空间方程的关系
对状态空间方程进行拉氏变换,带入0状态,得到
\[
sX(s)=AX(s)+BU(s)\,\,\,\,\,\,\, Y(s)=CX(s)+DU(s)
\]
将X(s)用U(s)带入,得到
\[
Y(s)=\left(C(sI-A)^{-1}B+D\right)U(s)
\]
即传递矩阵为\(C(sI-A)^{-1}B+D\)
例:求状态空间表达式
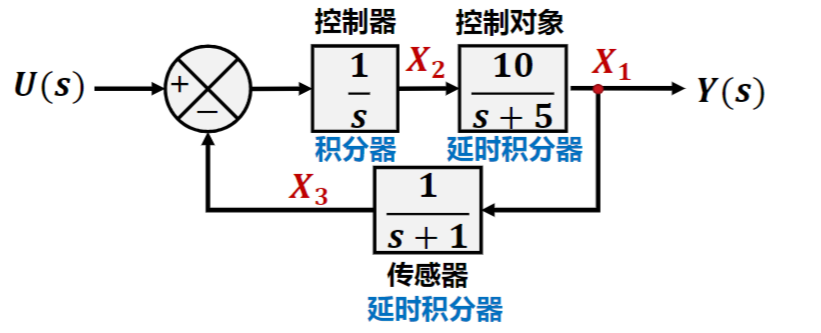
首先得到\(Y=X_1=\frac{10}{s+5}X_2,X_3=\frac{1}{s+1}X_1,X_2=(U-X_3)/s\)
由于复频域状态空间方程形式为\(sX(s)=AX(s)+BU(s)\),将上面等式化为
\[
sX_1=-5X_1+10X_2, sX_2=U(s)-X_3, sX_3=X_1-X_3
\]
易得矩阵